какую форму имеет гармонический сигнал
Максимально просто о гармониках и проблемах, возникающих от них
Анонс: Что такое гармонические искажения, гармоники и как они влияют на стабильность электроснабжения и качество электроэнергии в сети. Эмиссия гармонических искажений силовым оборудованием, проблемы технических средств компенсации реактивной мощности и фильтров гармоник.
В идеале любой источник питания, в том числе ТП распределительной сети, должен стабильно давать ток идеально синусоидального напряжения в каждом месте силовой сети абонента-потребителя, однако по ряду причин электросетевым компаниям часто бывает трудно обеспечить такие условия из-за эмиссии и трансмиссии гармонических искажений. Гармонические искажения тока, напряжения далеко не новость, но в настоящее время они представляют собой одну из основных проблем, вызывающих нарушения стабильности электроснабжения и качества электроэнергии в электроэнергетике.
В первых электроэнергетических системах гармонические искажения в основном вызывались насыщением трансформаторов, промышленных дуговых печей, мощных электросварочных аппаратов и т. п., а сами гармоники представляли сравнительно небольшую проблему из-за консервативной конструкции силового оборудования. Сегодня все более широкое использование нелинейных нагрузок в силовых сетях промышленных и непромышленных объектов обуславливает увеличение объемов гармонических искажений в распределительных сетях, причем именно через распределительные сети из-за «перегенерации» искажений трансформаторами ТП электросетевой компании силовые сети абонентов обмениваются гармониками между собой, (трансмиссия).
Наиболее часто используемой нелинейной нагрузкой является, пожалуй, ШИМ-преобразователь, широко используемый в сталелитейной, бумажной и текстильной промышленности, в приводах управление скоростью электродвигателя.

Наряду с этим, свой вклад в засорение сетей гармониками вносят системы энергосберегающего освещения, электроника центров обработки данных, программно-технических комплексов АСУ, электрические транспортные системы, бытовые электроприборы и т. д. К 2000 году было зафиксировано, что на электронные нагрузки приходилось около половины спроса на электроэнергию в США и развитых странах мира, а за два десятка лет нового века эта доля возросла до 70-80 %, и это вывело проблему гармонических искажений в перечень приоритетных и критических.
Для справки
Упрощенно, нелинейные нагрузки — это нагрузки, в которых форма волны тока не похожа на форму волны приложенного напряжения по ряду причин, например, из-за использования электронных переключателей, которые проводят ток только в течение части периода промышленной частоты и, следовательно, здесь закон Ома не может описать связь между напряжением и током. Среди наиболее распространенных нелинейных нагрузок — все типы выпрямительных устройств, в том числе источники бесперебойного питания, преобразователи напряжения компьютеров, частотно-регулируемые приводы, электрические печи, люминесцентные лампы и т. д. Нелинейные нагрузки вызывают искажение формы сигнала напряжения, перегрев трансформаторов и других силовых устройств, перегрузку по току проводов и клемм соединения оборудования, телефонные помехи, сбои в управлении микропроцессорами и пр.
Сам термин «гармоники» заимствован из области акустики, где он был связан с вибрацией струны или молекул воздуха с частотой, кратной базовой частоте, а гармоническая составляющая в системе питания переменного тока определяется как синусоидальная составляющая периодической формы волны, частота которой равна целому кратному основной частоте системы. Тогда гармоники в формах волны напряжения или тока можно представить, как идеально синусоидальные составляющие частот, кратных основной частоте: fn=(n)·f1, где n — порядок гармоники. Т. е. для наших сетей с f1=50 Гц частота третьей (n = 3) гармоники будет f3=3·50=150 Гц, пятой (n=5) f5=5·50=250 Гц, седьмой (n=7) f7=7·50=350 Гц и т. д. Хотя кривые зависимости тока на фундаментальной частоте и токов гармоник имеют форму синусоиды, результирующая кривая искажена из-за взаимного влияния токов разных частот (см. на рис. ниже).

Ситуация стала более сложной с применением конденсаторных батарей, используемых на промышленных предприятиях для коррекции коэффициента мощности, и энергокомпаниями для стабилизации напряжения вдоль распределительных линий. Результирующее реактивное сопротивление емкости образует колебательный контур с индуктивным реактивным сопротивлением системы на определенной (резонансной) частоте, которая может совпадать с одной из характеристических гармоник нагрузки, что обуславливает значительный наброс токов гармоник, перенапряжения, способные повредить изоляцию. По факту далеко не решает проблему в полном объеме использование активных фильтров гармоник (АФГ), по сути, тех же ШИМ-преобразователей (инвертеров), которые демпфируют гармоники противофазными токами «ниже» места присоединения, а для силовой сети «выше» остаются источниками эмиссии гармонических искажений.
Такая ситуация ставит перед инженерами сложную задачу по выявлению и исправлению чрезмерных уровней гармонических искажений формы сигналов тока и напряжения от стадии планирования до стадии проектирования энергетических и промышленных установок, что позволит не только поддерживать сети и оборудование в оптимальных условиях эксплуатации, но и предвидеть потенциальные проблемы с интеграцией, модернизацией нелинейных нагрузок, а также технических средств для нивелирования перетоков реактивной мощности и/или фильтров гармоник.
Гармонические колебания
На хабре было несколько статей по преобразованию Фурье и о всяких красивостях типа Цифровой Обработки Сигналов (ЦОС), но неискушённому пользователю совершенно не понятно, зачем всё это нужно и где, а главное как это применить.

АЧХ шума.
Лично мне после прочтения этих статей (например, этой ) не стало понятно, что это и зачем оно нужно в реальной жизни, хотя было интересно и красиво.
Хочется не просто поглядеть красивые картинки, а так сказать, ощутить нутром, что и как работает. И я приведу конкретный пример с генерацией и обработкой звуковых файлов. Можно будет и послушать звук, и поглядеть его спектр, и понять, почему это так.
Статья не будет интересна тем, кто владеет теорией функций комплексной переменной, ЦОС и прочими страшными темами. Она скорее для любопытствующих, школьников, студентов и им сочувствующих :).
Сразу оговорюсь, я не математик, и многие вещи могу даже сказать неправильно (поправляйте личным сообщением), и данную статью пишу, опираясь на собственный опыт и собственное понимание текущих процессов. Если вы готовы, то поехали.
Пару слов о матчасти
Если мы вспомним школьный курс математики, то для построения графика синуса мы использовали круг. В общем-то так и получается, что вращательное движение можно превратить в синусоиду (как и любое гармоническое колебание). Самое лучшая иллюстрация этого процесса приведена в википедии

Гармонические колебания
Т.е. фактически график синуса получается из вращения вектора, который описывается формулой:
где A — длина вектора (амплитуда колебаний), φ — начальный угол (фаза) вектора в нулевой момент времени, ω — угловая скорость вращения, которая равна:
ω=2 πf, где f — частота в Герцах.
Как мы видим, что зная частоту сигнала, амплитуду и угол, мы можем построить гармонический сигнал.
Магия начинается тогда, когда оказывается, что представление абсолютно любого сигнала можно представить в виде суммы (зачастую бесконечной) различных синусоид. Иначе говоря, в виде ряда Фурье.
Я приведу пример из английской википедии. Для примера возьмём пилообразный сигнал.

Пилообразный сигнал
Его сумма будет представлена следующей формулой:
Если мы будем по очерёдно суммировать, брать сначала n=1, затем n=2 и т.д., то увидим, как у нас гармонический синусоидальный сигнал постепенно превращается в пилу:
Наверное красивее всего это иллюстрирует одна программа, найденная мной на просторах сети. Выше уже говорилось, что график синуса является проекцией вращающегося вектора, а как же быть в случае более сложных сигналов? Это, как ни странно, проекция множества вращающихся векторов, а точнее их суммы, и выглядит это всё так:

Вектора рисуют пилу.
Вообще рекомендую сходить самим по ссылке и попробовать самим поиграться с параметрами, и посмотреть как меняется сигнал. ИМХО более наглядной игрушки для понимания я ещё не встречал.
Ещё следует заметить, что есть обратная процедура, позволяющая получить из данного сигнала частоту, амплитуду и начальную фазу (угол), которое называется Преобразование Фурье.

Разложение в ряд Фурье некоторых известных периодических функций (отсюда)
Я детально на нём останавливаться не буду, но покажу, как это можно применить по жизни. В списке литературы порекомендую то, где можно почитать подробнее о матчасти.
Переходим к практическим упражнениям!
Мне кажется, что каждый студент задаётся вопросом, сидя на лекции, например по матану: зачем мне весь этот бред? И как правило, не найдя ответа в обозримом будущем, к сожалению, теряет интерес к предмету. Поэтому я сразу покажу практическое применение данных знаний, а вы эти знания уже будете осваивать сами :).
Всё дальнейшее я буду реализовывать на сях. Делал всё, конечно, под Linux, но никакой специфики не использовал, по идее программа будет компилироваться и работать под другими платформами.
Для начала напишем программу для формирования звукового файла. Был взят wav-файл, как самый простой. Прочитать про его структуру можно тут.
Если кратко, то структура wav-файла описывается так: заголовок, который описывает формат файла, и далее идёт (в нашем случае) массив 16-ти битных данных (остроконечник) длиной: частота_дискретизации*t секунд или 44100*t штук.
Для формирования звукового файла был взят пример здесь. Я его немного модифицировал, исправил ошибки, и окончательная версия с моими правками теперь лежит на гитхабе тут
Сгенерируем двухсекундный звуковой файл с чистым синусом частотой 100 Гц. Для этого модифицируем программу таким образом:
Обращаю внимание, что формула чистого синуса соответствует той, о которой мы говорили выше. Амплитуда 32000 (можно было взять 32767) соответствует значению, которое может принимать 16-ти битное число (от минус 32767 до плюс 32767).
В результате получаем следующий файл (можно его даже послушать любой звуковоспроизводящей программой). Откроем данный файл audacity и увидим, что график сигнала в действительности соответствует чистому синусу:

Чистый ламповый синус
Поглядим спектр этого синуса (Анализ->Построить график спектра)

График спектра
Виден чистый пик на 100 Гц (логарифмический масштаб). Что такое спектр? Это амплитудно-частотная характеристика. Существует ещё фазочастотная характеристика. Если помните, выше я говорил, что для построения сигнала надо знать его частоту, амплитуду и фазу? Так вот, можно из сигнала получить эти параметры. В данном случае у нас график соответствий частот амплитуде, при чём амплитуда у нас не в реальных единицах, а в Децибелах.
Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять.
В данном случае просто логарифм амплитуды, умноженный на 10. Логарифмический масштаб удобно использовать при работе с сигналами.
Мне, честно говоря, не очень нравится анализатор спектра в этой программе, поэтому я решил написать свой с блекджеком и шлюхами, тем более, что это несложно.
Пишем свой анализатор спектра
Здесь может быть скучно, поэтому можете перейти сразу к следующей главе.
Поскольку я прекрасно понимаю, что тут портянки кода размещать нет смысла, те, кому реально интересно — сами найдут и поковыряют, а тем, кому это неинтересно, будут скучать, то я остановлюсь только на основных моментах написания анализатора спектра wav-файла.
Во-первых, нам wav-файл необходимо читать. Там необходимо прочитать заголовок, чтобы понять, что содержит данный файл. Я не стал реализовывать море вариантов чтения данного файла, а остановился только на одном. Пример чтения файла был взят отсюда практически без изменений, ИМХО — отличный пример. Там же есть реализация на питоне.
Следующее, что нам нужно, это быстрое преобразование Фурье. Это то самое преобразование, которое позволяет получить из конечного набора точек вектора исходных сигналов. Пусть вас пока это не пугает, дальше я объясню.
Опять же, велосипед изобретать не стал, а взял готовый пример отсюда.
Я понимаю, что чтобы объяснить, как работает программа, надо объяснить, что такое быстрое преобразование Фурье, а это как минимум ещё на одну некислую статью.
Для начала алокируем массивы:
Скажу лишь, что в программе мы читаем данные в массив длиной size_array (которое берём из заголовка wav-файла).
Массив для быстрого преобразования Фурье должен представлять собой последовательность
Амплитудно-частотная характеристика (АЧХ). Спектр сигнала.
При обсуждении переменного тока в одной из предыдущих статей (ссылка) мы познакомились с понятием гармонической (синусоидальной) функции. А бывают ли негармонические функции и сигналы и как с ними работать? В этом нам и предстоит сегодня разобраться 🙂 Кроме того, мы рассмотрим важнейшее понятие — амплитудно-частотную характеристику (АЧХ) сигналов.
Гармонические и негармонические сигналы.
Здесь A — амплитуда сигнала, w — циклическая частота, а \phi — начальная фаза. Вы спросите — а как же синус? Разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что sin\alpha = cos(\frac<\pi><2>\medspace-\medspace \alpha) — то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний 🙂
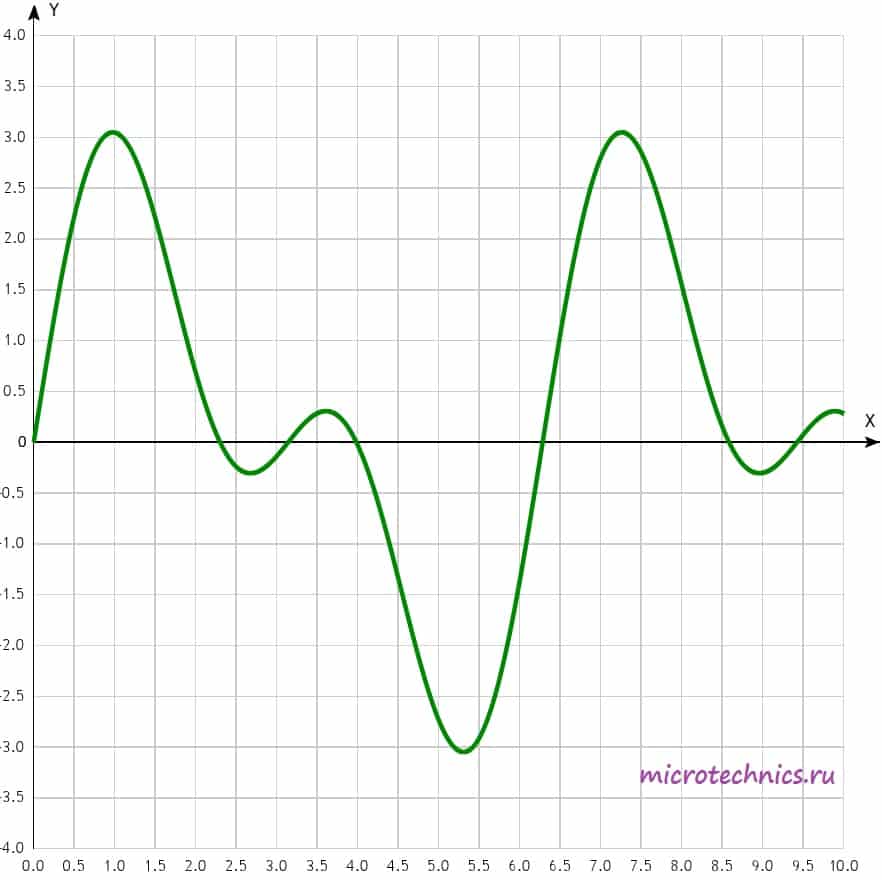
Вторым подклассом периодических сигналов являются негармонические колебания. Вот пример негармонического сигнала:
Как видите, несмотря на «нестандартную» форму, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.
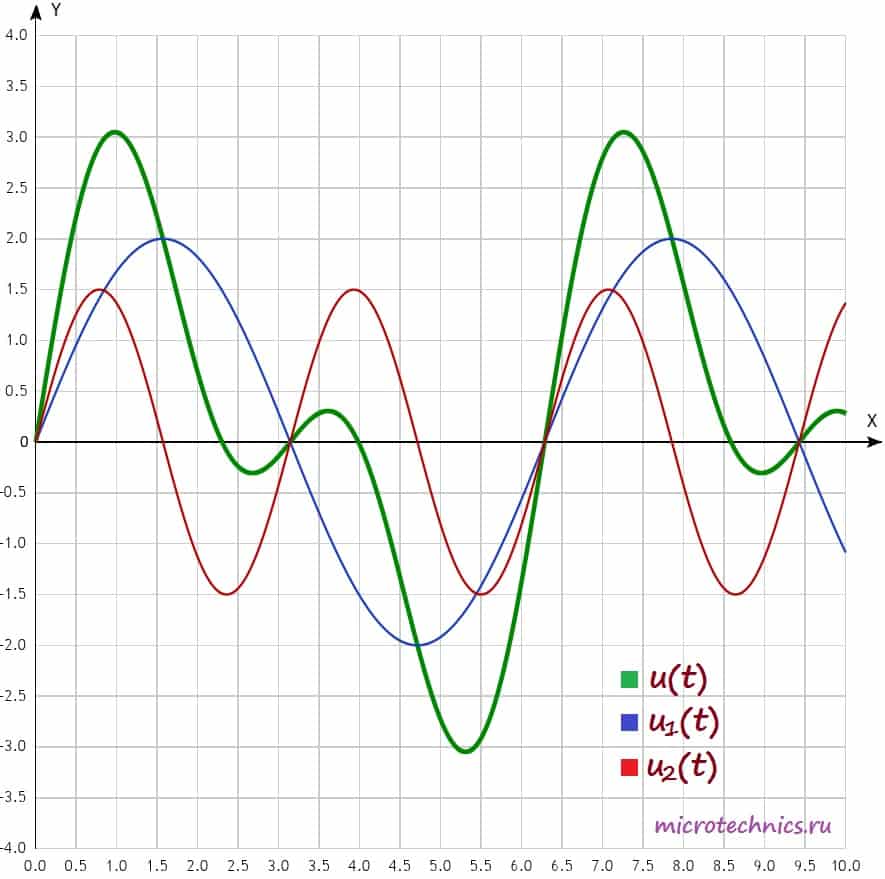
Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье. Суть методики состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что давайте рассмотрим практический пример и разберемся чуть подробнее 🙂 Для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:
Давайте изобразим все эти сигналы на одном графике:
В этой формуле U_k — амплитуда, а \phi_k — начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и видим в этой формуле 🙂 U_0 — это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите — среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме U_0 будут равны 0.
Амплитудный спектр сигнала.
Совокупность всех гармонических составляющих негармонического сигнала называют спектром этого сигнала. Различают фазовый и амплитудный спектр сигнала:
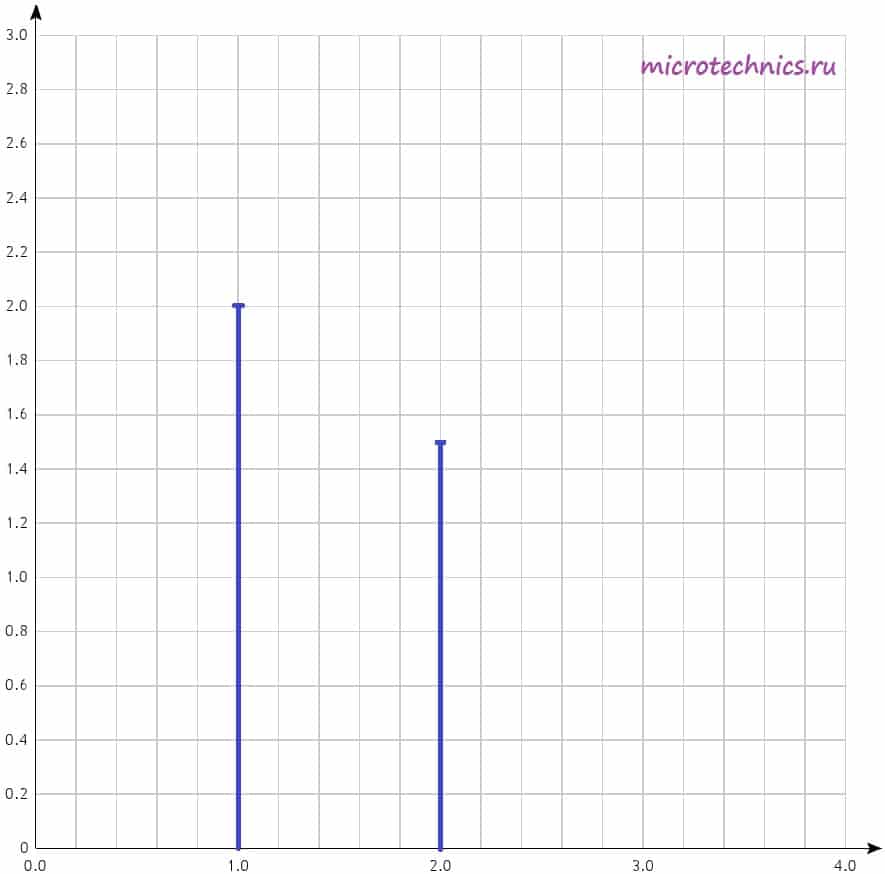
Давайте рассмотрим амплитудный спектр поподробнее. Для визуального изображения спектра используют диаграммы, представляющие из себя набор вертикальных линий определенной длины (длина зависит от амплитуды сигналов). На горизонтальной оси диаграммы откладываются частоты гармоник:
По горизонтальной оси могут откладываться как частоты в Гц, так и просто номера гармоник, как в данном случае. А по вертикальной оси — амплитуды гармоник, тут все понятно. Давайте построим амплитудный спектр сигнала для негармонического колебания, которое мы рассматривали в качестве примера в самом начале статьи. Напоминаю, что его разложение в ряд Фурье выглядит следующим образом:
У нас есть две гармоники, амплитуды которых равны, соответственно, 2 и 1.5. Поэтому на диаграмме две линии, длины которых соответствуют амплитудам гармонических колебаний. Фазовый спектр сигнала строится аналогично, за той лишь разницей, что используются начальные фазы гармоник, а не амплитуды.
Итак, с построением и анализом амплитудного спектра сигнала мы разобрались! Давайте перейдем к следующей теме сегодняшней статьи — к понятию амплитудно-частотной характеристики.
Амплитудно-частотная характеристика (АЧХ).
АЧХ является важнейшей характеристикой многих цепей и устройств — фильтров, усилителей звука и т. д. Даже простые наушники имеют свою собственную амплитудно-частотную характеристику. Что же она показывает?
АЧХ — это зависимость амплитуды выходного сигнала от частоты входного сигнала. Как мы выяснили в первой части статьи, негармонический периодический сигнал можно разложить в ряд Фурье. Но нас сейчас интересует, в первую очередь, аудио-сигнал, и выглядит он следующим образом:
Как видите, ни о какой периодичности здесь не идет и речи! Но, к счастью, существуют специальные алгоритмы, которые позволяют представить звуковой сигнал в виде спектра входящих в него частот. Мы сейчас не будем подробно разбирать эти алгоритмы, это тема для отдельной статьи 🙂 Просто примем тот факт, что они позволяют нам осуществить такое преобразование с аудио-сигналом.
Соответственно, мы можем построить диаграмму амплитудного спектра звукового сигнала. А пройдя через какую-либо цепь (к примеру, через наушники при воспроизведении звука) сигнал будет изменен. Так вот амплитудно-частотная характеристика как раз и показывает, какие изменения будет претерпевать входной сигнал при прохождении через ту или иную цепь. Давайте обсудим этот момент чуть поподробнее…
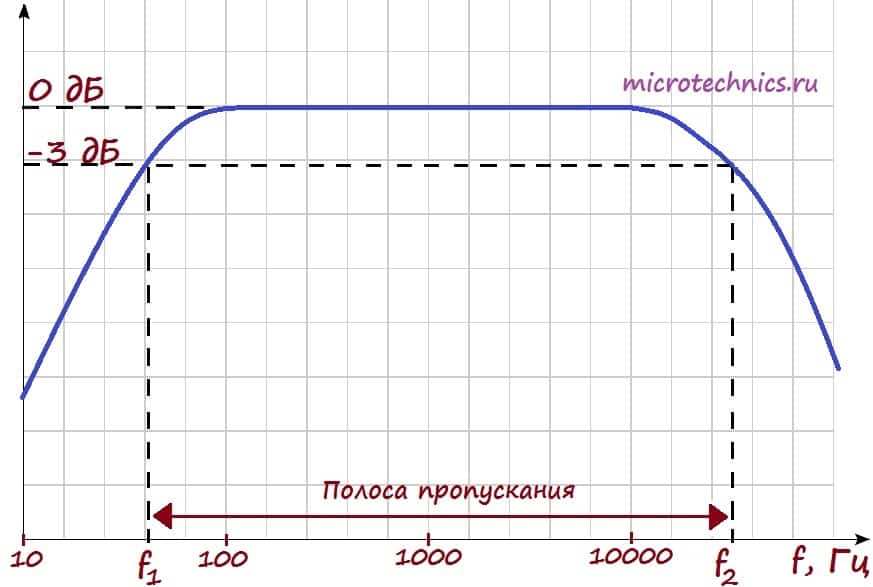
Итак, на входе мы имеем ряд гармоник. Амплитудная-частотная характеристика показывает, как изменится амплитуда той или иной гармоники при прохождении через цепь. Рассмотрим пример АЧХ:
Разберемся поэтапно, что же тут изображено… Начнем с осей графика АЧХ. По оси y мы откладываем величину выходного напряжения (или коэффициента усиления, как на данном рисунке). Коэффициент усиления мы откладываем в дБ, соответственно величина, равная 0 дБ, соответствует усилению в 1 раз, то есть амплитуда сигнала остается неизменной.
По оси x откладываются частоты входного сигнала. Таким образом, в рассматриваемом случае для всех гармоник, частоты которых лежат в интервале от 100 до 10000 Гц, амплитуда не изменится. А сигналы всех остальных гармоник будут ослаблены.
Практические примеры АЧХ аудио-устройств.
Частотный диапазон аудио-устройств обычно разбивают на низкие, средние и высокие частоты. Приблизительно это выглядит так:
Именно такую терминологию обычно можно встретить в разных программах-эквалайзерах, используемых для настройки звука. Теперь вы знаете, что красивые графики из таких программ являются именно амплитудно-частотными характеристиками, с которыми мы познакомились в сегодняшней статье 🙂
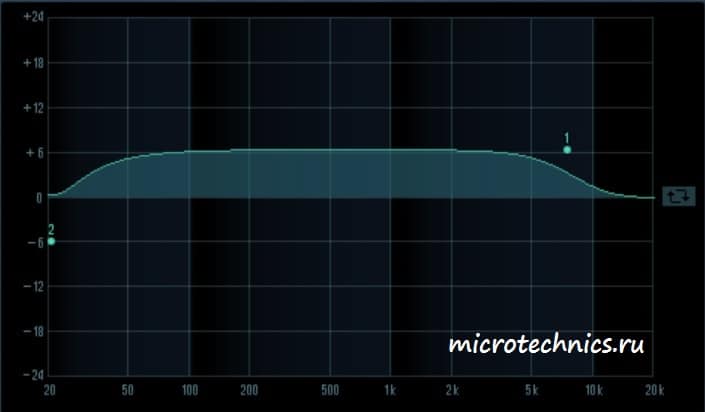
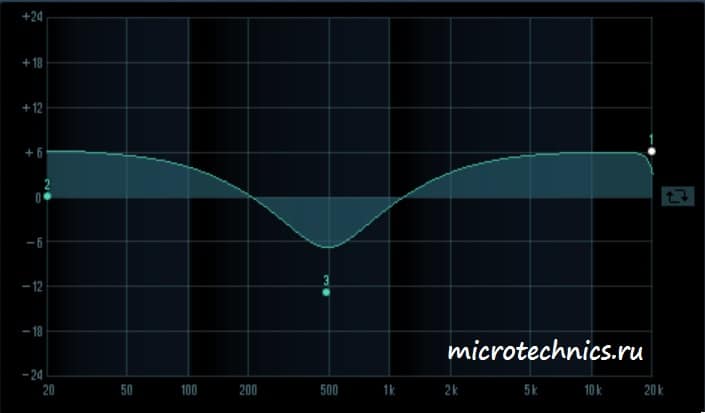
В завершении статьи посмотрим на пару АЧХ, полученных в программном эквалайзере:
Здесь мы можем видеть амплитудно-частотную характеристику усилителя. Причем усилены будут преимущественно средние частоты диапазона.
А здесь ситуация совсем другая — низкие и верхние частоты усиливаются, а в области средних частот для гармоник с частотой 500 Гц мы наблюдаем значительное ослабление.
А здесь усиливаются только низкие частоты. Аудио-аппаратура с такой АЧХ будет обладать высоким уровнем басов 🙂
На этом мы заканчиваем нашу сегодняшнюю статью… Спасибо за внимание и ждем вас на нашем сайте снова!
Гармонические составляющие сети. Что это такое и как с ними быть
2020-12-17 

Как нам хорошо известно, сетевое напряжение имеет синусоидальную форму и частоту равную 50 Гц. Это в идеале, но на практике так бывает далеко не всегда. И дело здесь в гармонических составляющих сети — высших гармониках, представляющих из себя частотные сигналы, отличающиеся от основной частоты, и вносящих искажения в синусоидальную форму питающего напряжения, а это в свою очередь становится причиной ухудшения качества электроэнергии, нарушению нормальной работы электропотребителей и т.д.
Откуда же берутся эти гармонические составляющие?
Дело в том, что в цепях с линейной нагрузкой, к которым можно отнести сопротивление, индуктивность, емкость, протекающий через нагрузку ток пропорционален прикладываемому напряжению и следовательно синусоидальной форме сигнала напряжения соответствует токовая синусоида, поэтому разность фаз между ними равна нулю. А вот в случае, если наблюдается нелинейная зависимость протекающего тока от приложенного напряжения, синусоидальная форма сигнала искажается.
Связано это в первую очередь с ростом количества электрооборудования, имеющего нелинейные характеристики, вызванные наличием в схемотехнике полупроводниковых элементов. Наиболее «проблемными» в этом плане являются тиристорные регуляторы, преобразователи частоты, источники бесперебойного питания, электронные балласты, сварочные аппараты, электродуговые печи и другое оборудование с импульсными источниками питания.
Это приводит к возникновению импульсных токов, содержащих большое количество гармонических составляющих, так называемых высших гармоник, отличающихся от основной гармоники, которые затем попадают в электрические сети и вносят искажения. Гармоники образуются на частотах, кратных основной. Так, первая (основная) гармоника имеет частоту 50 Гц, частота гармоники 3-го порядка будет равна 150 Гц, частота гармоники 5-го порядка – 250 Гц и т.д. Получается, что реальное напряжение в сети представляет собой сумму основного синусоидального сигнала и его гармонических составляющих.
Надо учитывать, что полностью избавиться от влияния гармонических составляющих невозможно, и пока уровень гармоник не превышает допустимых норм, в принципе можно не беспокоиться о каких-то серьезным последствиях. Согласно ГОСТ 13109-97, нормально допустимое значение коэффициентов гармонических составляющих напряжения для сетей 0,38 кВ составляет 8 %, а предельно допустимое — 12 %. Также в этом ГОСТ приведены допустимые значения для каждой n-ой гармонической составляющей, например для 3-ей гармоники это 5%, для 5-ой гармоники – 6,0 %, для 7-ой гармоники – 5 % и т.д. Считается, что наибольшие искажения в синусоидальный сигнал вносят гармоники 3, 5, 7 порядка.
Немного расчётов
Параметр, указывающий на уровень влияния нелинейных искажений, или по другому степень отличия формы сигнала от синусоидальной, называется коэффициентом нелинейных искажений Ku (THD — Total Harmonic Distorsions).
U (1) – действующее значение напряжения 1-ой гармоники
U (2), U (3) … U (40) – действующие значения напряжения высших гармоник.
Таким образом можно определить общую долю суммарного напряжения высших гармоник по отношению к напряжению основной частоты.
Еще одним параметром является коэффициент n-ой гармонической составляющей напряжения
n — номер гармонической составляющей, кратной основной частоте
По этой формуле вычисляется вклад конкретной гармоники в общие искажения.
Основные характеристики гармоник
Все гармоники можно разделить по трем основным характеристикам — порядковому номеру, частоте и типу последовательности.
Последствия возникновения
Какие же проблемы приносят гармонические составляющие в случае отклонения от предельно допустимых показателей?
На самом деле негативных воздействий немало, это увеличение потерь в сетях, перегрев трансформаторов,перегрузки на нейтральных проводах, гармонические шумы, искажение формы синусоидальной кривой, перегрузка и следовательно уменьшение срока службы конденсаторов коррекции коэффициента мощности, поверхностный эффект. И это еще перечислены не все негативные последствия данного эффекта. Все эти факторы приводят в конечном итоге к экономическим, энергетическим потерям и сокращению срока службы оборудования.
Измерение показателей гармоник в сети
Для анализа качества электросети и выявления высших гармоник применяются, в частности, многофункциональные измерительные приборы или по другому анализаторы качества электроэнергии.
Они позволяют получать подробную информацию по всем основным характеристикам качества электроэнергии, таким как:
И целый ряд других параметров, которые по совокупности позволяют получить точную оценку не только гармонических величин, но и провести полный анализ состояния сетей.
Кроме этого, анализаторы имеют дополнительные функции, такие как ведение журнала событий, проверка последовательности чередования фаз, передача данных на верхний уровень по интерфейсу RS-485 или Ethernet, светодиодная индикация, дискретные входы и выходы.
Способы уменьшения гармонических составляющих
На основании полученных данных можно принимать решения о внедрении средств, направленных на уменьшение гармонических составляющих.
К основным способам уменьшения гармоник относятся разделение линейных и нелинейных нагрузок, обеспечение симметричного режима работы трехфазной системы, снижение полного сопротивления распределительной сети за счет увеличения сечения кабелей, применение линейных дросселей, применение изолирующих трансформаторов с обмотками «треугольник» и «звезда», применение пассивных и активных фильтров.
Одним из наиболее простых способов снижения уровня высших гармоник является установка линейных дросселей переменного тока. В частности, такой способ фильтрации широко применяется для подавления помех, возникающих при работе частотных преобразователей.
Дроссель имеет малое значение индуктивного сопротивления на основной частоте 50 Гц и большое значение сопротивления для высших гармоник, что приводит к их ослаблению. Помимо дросселей переменного тока, для частотных преобразователей могут применяться и дроссели звена постоянного тока.
Помимо дросселей широко применяются пассивные и активные фильтры.
Пассивный фильтр гармоник
Пассивные фильтры строятся на основе индуктивно-емкостной схемы (LC-фильтры), состоящей из продольных индуктивностей и поперечной цепи, состоящей из последовательно включенных индуктивности и емкости которые образуют последовательный колебательный контур, настроенный на определенную гармонику. Если необходимо уменьшение коэффициента искажения по нескольким гармоникам, можно использовать несколько параллельно включенных фильтров. Такой метод часто используется в цепях с источниками бесперебойного питания ( UPS).
Недостатком такого метода является его ограниченный только определенными гармониками эффект, поэтому для подавления всего спектра гармонических составляющих в сети используются активные фильтры.
Активный фильтр гармоник
Активный фильтр гармоник (АФГ) представляет собой электронное устройство, можно сказать является управляемым источником тока, подключаемым параллельно с нагрузкой, генерирующей высшие гармоники. Принцип действия основан на анализе гармоник нелинейной нагрузки и генерировании в распределительную сеть таких же гармоник, но противофазе. В результате высшие гармонические составляющие нейтрализуются в точке подключения фильтра и на выходе получается почти синусоидальная форма.
Такой метод благодаря своей эффективности является одним из наиболее действенных способов подавления высших гармоник, но не самым дешевым. Его применение оправдано там, где наблюдается большой уровень искажений.