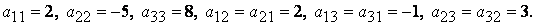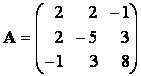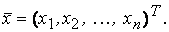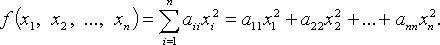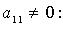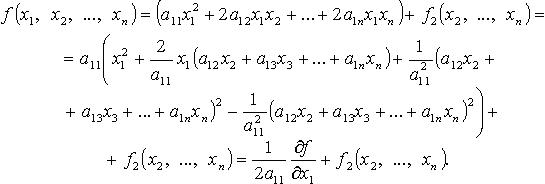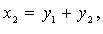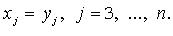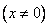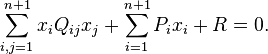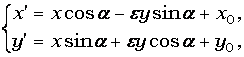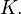канонический и нормальный вид квадратичной формы
Квадратичные формы и квадрики



Понятие квадратичной формы. Матрица квадратичной формы. Канонический вид квадратичной формы. Метод Лагранжа. Нормальный вид квадратичной формы. Ранг, индекс и сигнатура квадратичной формы. Положительно определенная квадратичная форма. Квадрики.
Понятие квадратичной формы: функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.
Квадратичной формой 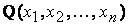
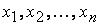
Матрица квадратичной формы: Матрицу 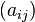
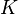
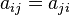
Написать матрицу квадратичной формы:
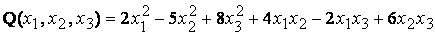
Здесь
В векторно-матричной форме квадратичная форма имеет вид:
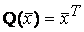
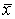
Канонический вид квадратичной формы: Квадратичная форма называется канонической, если все 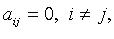
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.
Метод Лагранжа: последовательное выделение полных квадратов. Например, если
Затем подобную процедуру проделывают с квадратичной формой 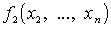
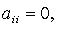
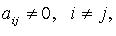
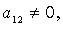
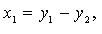
Ранг, индекс и сигнатура квадратичной формы: Рангом квадратичной формы 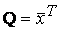
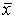
Положительно определенная квадратичная форма: Вещественная квадратичная форма 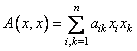
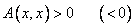
В этом случае матрица 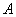
Класс положительно определенных (отрицательно определенных) форм является частью класса неотрицательных (соответственно неположительных) форм.
Квадрики: Квадрик — n-мерная гиперповерхность в n+1-мерном пространстве, заданная как множество нулей многочлена второй степени. Если ввести координаты <x1, x2, xn+1> (в евклидовом или аффинном пространстве), общее уравнение квадрики имеет вид [1]
Это уравнение можно переписать более компактно в матричных обозначениях:
где x = <x1, x2, xn+1> — вектор-строка, x T — транспонированный вектор, Q — матрица размера (n+1)×(n+1) (предполагается, что хотя бы один её элемент ненулевой), P — вектор-строка, а R — константа. Наиболее часто рассматривают квадрики над действительнымиили комплексными числами. Определение можно распространить на квадрики в проективном пространстве, см. ниже.
Более общо, множество нулей системы полиномиальных уравнений известно как алгебраическое многообразие. Таким образом, квадрика является (аффинным или проективным) алгебраическим многообразием второй степени и коразмерности 1.
Преобразования плоскости и пространства.
Определение преобразования плоскости. Определение движения. свойства движения. Два вида движений: движение I рода и движение II рода. Примеры движений. Аналитическое выражение движения. Классификация движений плоскости (в зависимости от наличия неподвижных точек и инвариантных прямых). Группа движений плоскости.
Определение преобразования плоскости: Определение. Преобразование плоскости сохраняющее расстояние между точками называется движением (или перемещением) плоскости. Преобразование плоскости называется аффинным, если оно любые три точки, лежащие на одной прямой переводит в три точки также лежащие на одной прямой и при этом сохраняет простое отношение трех точек.
Определение движения: это преобразования фигур, при котором сохраняются расстояния между точками. Если две фигуры точно совместить друг с другом посредством движения, то эти фигуры одинаковы, равны.
Свойства движения: всякое сохраняющее ориентацию движение плоскости является либо параллельным переносом, либо поворотом, всякое меняющее ориентацию движение плоскости является либо осевой симметрией, либо скользящей симметрией. Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения. При движении сохраняются углы между полупрямыми.
Композицией любого числа движений первого рода является движение первого рода.
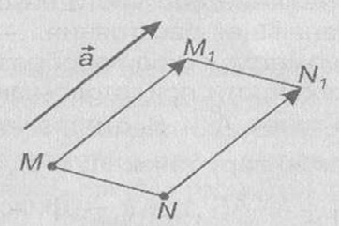
Примеры движений: Параллельный перенос . Пусть а — данный вектор. Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка М отображается в точку М1, что вектор MМ1 равен вектору а.
Параллельный перенос является движением, поскольку представляет собой отображение плоскости на себя, сохраняющее расстояния. Наглядно это движение можно представить как сдвиг всей плоскости в направлении данного вектора а на его длину.
Поворот является движением, поскольку представляет собой отображение плоскости на себя, при котором сохраняются расстояния.
Аналитическое выражение движения: аналитическая связь, между координатами прообраза и образа точки имеет вид (1).
Классификация движений плоскости (в зависимости от наличия неподвижных точек и инвариантных прямых): Определение:
Точка плоскости инвариантной (неподвижной), если при данном преобразовании она переходит в себя.
Пример: При центральной симметрии инвариантной является точка центра симметрии. При повороте инвариантной является точка центра поворота. При осевой симметрии инвариантной является прямая — ось симметрии — это прямая инвариантных точек.
Теорема: Если движение не имеет ни одной инвариантной точки, то оно имеет хотя бы одно инвариантное направление.
Пример: Параллельный перенос. Действительно, прямые, параллельные этому направлению инвариантных как фигура в целом, хотя не состоит из инвариантных точек.
Теорема: Если движется какой-то луч, луч переводит в себя, то это движение либо тождественное преобразование, либо симметрия относительно прямой содержащей данный луч.
Поэтому по наличию инвариантных точек или фигур можно провести классификацию движений.
Группа движений плоскости: В геометрии важную роль играют группы самосовмещений фигур. Если 
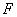
Это множество является группой. Например, для равностороннего треугольника 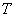
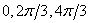
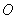
Они изображены на рис. 1 красными линиями. Элементы группы самосовмещений правильного треугольника могут быть заданы и иначе. Чтобы пояснить это, пронумеруем вершины правильного треугольника 
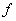
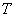
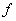
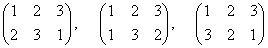
где числами 1, 2, 3 обозначены номера тех вершин, в которые переходят вершины 1, 2, 3 в результате рассматриваемого движения.
Проективные пространства и их модели.
Понятие проективного пространства и модели проективного пространства. Основные факты проективной геометрии. Связка прямых с центром в точке O – модель проективной плоскости 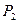
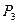
Понятие проективного пространства и модели проективного пространства:
Проективное пространство над полем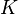
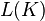
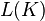
Если 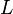
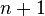
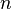
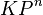
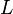
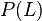
Переход от векторного пространства 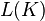
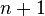
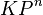
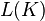
Точки 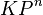
Основные факты проективной геометрии: Проективная геометрия — раздел геометрии, изучающий проективные плоскости и пространства. Главная особенность проективной геометрии состоит в принципе двойственности, который прибавляет изящную симметрию во многие конструкции. Проективная геометрия может изучаться как с чисто геометрической точки зрения, так с аналитической (с помощью однородных координат) и салгебраической, рассматривая проективную плоскость как структуру над полем. Часто, и исторически, вещественная проективная плоскость рассматривается как Евклидова плоскость с добавлением «прямой в бесконечности».
Тогда как свойства фигур, с которыми имеет дело Евклидова геометрия, являются метрическими (конкретные величины углов, отрезков, площадей), а эквивалентность фигур равнозначна их конгруэнтности (т.е. когда фигуры могут быть переведены одна в другую посредством движения с сохранением метрических свойств), существуют более «глубоко лежащие» свойства геометрических фигур, которые сохраняются при преобразованиях более общего типа, чем движение. Проективная геометрия занимается изучением свойств фигур, инвариатных при классе проективных преобразований, а также самих этих преобразований.
Проективная геометрия дополняет Евклидову, предоставляя красивые и простые решения для многих задач, осложнённых присутствием параллельных прямых. Особенно проста и изящна проективная теория конических сечений.
Есть три главных подхода к проективной геометрии: независимая аксиоматизация, дополнение Евклидовой геометрии, и структура над полем.
Аксиоматизация
Проективное пространство можно определить с помощью разного набора аксиом.
Коксетер предоставляет следующие:
1. Существует прямая и точка не на ней.
2. На каждой прямой есть по крайней мере три точки.
3. Через две точки можно провести ровно одну прямую.
4. Если A, B, C, и D — различные точки и AB и CD пересекаются, то AC и BD пересекаются.
5. Если ABC — плоскость, то существует по крайней мере одна точка не в плоскости ABC.
6. Две различные плоскости пересекаются по крайней мере в двух точках.
7. Три диагональные точки полного четырёхугольника не коллинеарны.
8. Если три точки на прямой X инвариантны по отношению к проективности φ, то все точки на X инвариантны по отношению к φ.
Проективная плоскость (без третьего измерения) определяется несколько другими аксиомами:
1. Через две точки можно провести ровно одну прямую.
2. Любые две прямые пересекаются.
3. Существует четыре точки, из которых нет трёх коллинеарных.
4. Три диагональные точки полных четырёхугольников не коллинеарны.
5. Если три точки на прямой X инвариантны по отношению к проективности φ, то все точки на X инвариантны по отношению к φ.
6. Теорема Дезарга: Если два треугольника перспективны сквозь точку, то они перспективны сквозь прямую.
При наличии третьего измерения, теорема Дезарга может быть доказана без введения идеальных точки и прямой.
Расширенная плоскость – модель проективной плоскости: возьмем в аффинном простран- стве A3 связку прямых S(O) с центром в точке O и плоскость Π, не проходя- щую через центр связки: O 6∈ Π. Связка прямых в аффинном пространстве является моделью проективной плоскости. Зададим отображение множества точек плоскости Π на множество прямых связки S (Бля, молись если достался этот вопрос, прости)
Расширенное трехмерное аффинное или евклидово пространство – модель проективного пространства 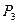
Изображения плоских и пространственных фигур при параллельном проектировании:
Таким образом, каждой точке A пространства сопоставляется ее проекция A‘ на плоскость p. Это соответствие называется параллельным проектированием на плоскость p в направлении прямой l.
Группа проективных преобразований. Приложение к решению задач.
Понятие проективного преобразования плоскости. Примеры проективных преобразований плоскости. Свойства проективных преобразований. Гомология, свойства гомологии. Группа проективных преобразований.
Понятие проективного преобразования плоскости: Понятие проективного преобразования обобщает понятие центральной проекции. Если выполнить центральную проекцию плоскости α на некоторую плоскость α1, затем проекцию α1 на α2, α2 на α3, … и, наконец, какой-то плоскости αn опять на α1, то композиция всех этих проекций и есть проективное преобразование плоскости α; в такую цепочку можно включить ипараллельные проекции.
Примеры проективных преобразований плоскости: Проективным преобразованием пополненной плоскости называется ее взаимно-однозначное отображение на себя, при котором сохраняется коллинеарность точек, или, другими словами, образом любой прямой является прямая. Всякое проективное преобразование есть композиция цепочки центральных и параллельных проекций. Аффинное преобразование – это частный случай проективного, при котором бесконечно удаленная прямая переходит сама в себя.
Свойства проективных преобразований:
При проективном преобразовании три точки не лежащие на прямой переходят в три точки не лежащие на прямой.
При проективном преобразовании репер переходит в репер.
При проективном преобразовании прямая переходит в прямую, пучок переходит в пучок.
Гомология, свойства гомологии:
Проективное преобразование плоскости, которое имеет прямую инвариантных точек, а значит, и пучок инвариантных прямых называется гомологией.
1. Прямая, проходящая через несовпадающие соответственные точки гомологии, является инвариантной прямой;
2. Прямые, проходящие через несовпадающие соответственные точки гомологии, принадлежат одному пучку, центр которого является инвариантной точкой.
3. Точка, ее образ и центр гомологии лежат на одной прямой.
Группа проективных преобразований: рассмотрим проективное отображение проективной плоскости P2 на себя, то есть проективное преобразование этой плоскости (P2’ = P2).
Как и прежде композицией f проективных преобразований f1 и f2 проективной плоскости P2 назовем результат последовательного выполнения преобразований f1 и f2: f = f2°f1.
Теорема 1: множество H всех проективных преобразований проективной плоскости P2 является группой относительно композиции проективных преобразований.
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Квадратичная форма
Определение
Пример. Функции
Оказывается, что в любой квадратичной форме можно так сгруппировать входящие в нее одночлены, что в результате получится ее (эквивалентное) представление в виде суммы квадратов.
Пример.
Метод Лагранжа приведения квадратичной формы к каноническому виду
Существует универсальный алгоритм, приводящий произвольную квадратичную форму к каноническому виду.
Пример. Привести форму
Пример. Привести форму
Пример. Привести форму
Матричная форма записи квадратичной формы
Задача. Установить правило формирования коэффициентов канонического вида квадратичной формы, получающегося применением метода Лагранжа.
Пример. Для приведенной выше квадратичной формы
| $ x_ <1>$ | $ x_ <2>$ | $ x_ <3>$ | |
|---|---|---|---|
| $ x_ <1>$ | $ f_ <11>$ | $ \frac<1><2>f_ <12>$ | $ \frac<1><2>f_ <13>$ |
| $ x_ <2>$ | $ \frac<1><2>f_ <12>$ | $ f_ <22>$ | $ \frac<1><2>f_ <23>$ |
| $ x_ <3>$ | $ \frac<1><2>f_ <13>$ | $ \frac<1><2>f_ <23>$ | $ f_ <33>$ |
Пример. Для
Вернемся к примерам предыдущего пункта, перепишем их на матричном языке.
Пример. Для формы
Поставленную в начале пункта задачу об установлении структуры канонического вида квадратичной формы попытаемся решить сначала для случая когда замену переменных можно подобрать именно в треугольном виде.
Метод Лагранжа и метод Гаусса
Пример. Рассмотрим матрицу квадратичной формы
Формула Якоби
Закон инерции для квадратичных форм
Для заданной квадратичной формы канонические виды, т.е. представления в виде сумм квадратов, можно построить разными способами. Выясним, какие характеристики являются общими (инвариантными) для этих представлений.
Ранг квадратичной формы
Ранг квадратичной формы равен числу ненулевых коэффициентов в ее каноническом виде.
Закон инерции
Теорема [закон инерции]. Индексы инерции не зависят от способа приведения квадратичной формы к каноническому виду.
Доказательство ☞ ЗДЕСЬ.
Доказательство следует из формулы Якоби.
Пример. Найти ранг и сигнатуру квадратичной формы
Рассмотренный только что пример относится к общей задаче оценки влияния параметров на характеристики квадратичной формы:
Как меняются ранг и сигнатура при непрерывном изменении параметров?
Справедливо и более общее утверждение.
Конгруэнтность квадратичных форм
Множество всех квадратичных форм с вещественными коэффициентами можно разбить на классы эквивалентности, в каждом из которых будут находиться только конгруэнтные между собой формы. Каждый из классов полностью описывается каким-то из своих представителей. Таким представителем можно взять нормальный вид.
Какое преобразование квадратичной формы оставляет ее инвариантной?
Знакоопределенность
Задача. Найти условия неотрицательности и положительной определенности квадратичной формы в терминах ее коэффициентов.
Теорема. Ненулевая квадратичная форма, представленная в правильном виде
Доказательство ☞ ЗДЕСЬ.
К счастью, явное представление канонического вида квадратичной формы уже имеется — как правило, он задается формулой Якоби. Индексы инерции вычисляются через знаки главных миноров матрицы квадратичной формы.
Теорема [Сильвестр]. Квадратичная форма
Доказательство ☞ ЗДЕСЬ.
Квадратичная форма будет отрицательно определенной тогда и только тогда, когда знаки главных миноров ее матрицы будут чередоваться следующим образом:
Пример. Квадратичная форма
Имеются ли конструктивные необходимые и достаточные условия неотрицательности квадратичной формы?
Теорема. Пусть линейное подпространство задано системой линейных однородных уравнений
Пример. Найти ортогональную замену переменных, приводящую квадратичную форму
Доказательство основано на правиле знаков Декарта.
Геометрия замен переменных
Оба преобразования координат не изменяют типа кривой: эллипс остается эллипсом. Но второе преобразование дает нечто большее: оно сохраняет размеры. Фактически, оно сводится к повороту исходного эллипса.