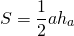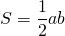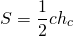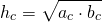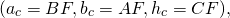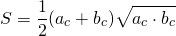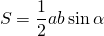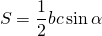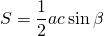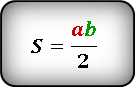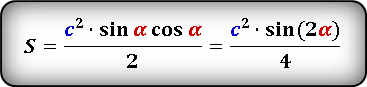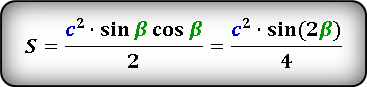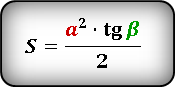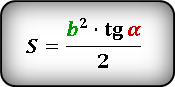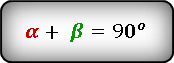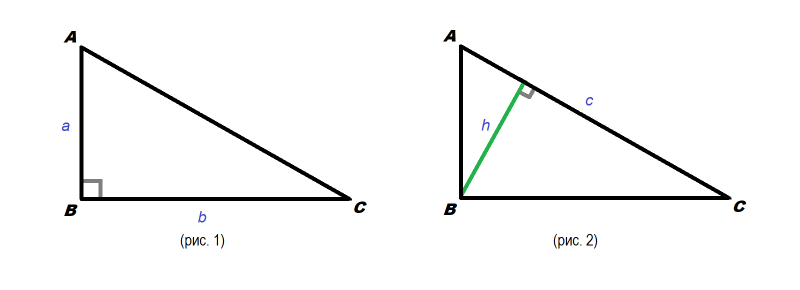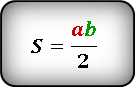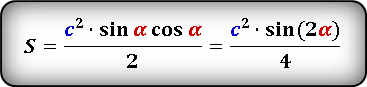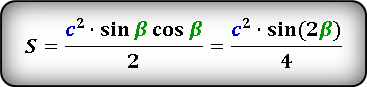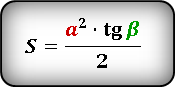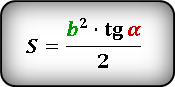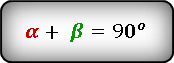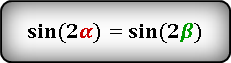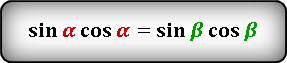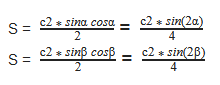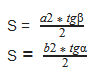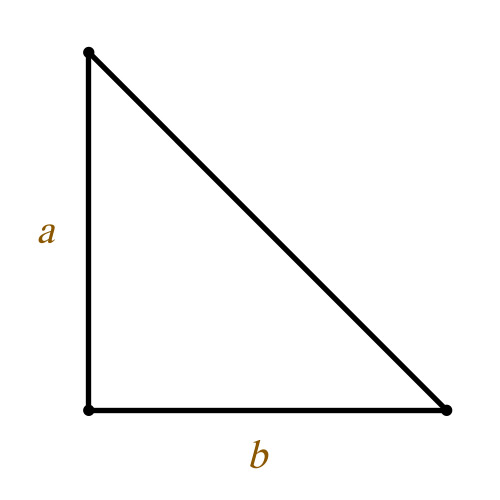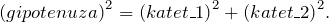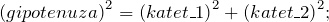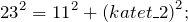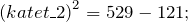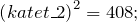Площадь прямоугольного треугольника как вычислить
Площадь прямоугольного треугольника как вычислить
Площадь прямоугольного треугольника
Как найти площадь прямоугольного треугольника?
Любая формула площади треугольника может быть использована и для вычисления площади прямоугольного треугольника.
Выведем формулы для нахождения площади прямоугольного треугольника через катеты, гипотенузу, острый угол, проекции катетов на гипотенузу.
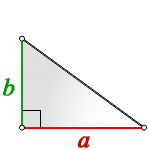
I. Площадь треугольника равна половине произведению стороны на высоту, проведенную у этой стороне:
Поскольку катеты перпендикулярны, то один катет является высотой, проведенной к другому катету.
Поэтому площадь прямоугольного треугольника равна половине произведения его катетов.
Формула для нахождения
площади прямоугольного
треугольника
через катеты
площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе.
Формула для нахождения площади прямоугольного треугольника по гипотенузе:
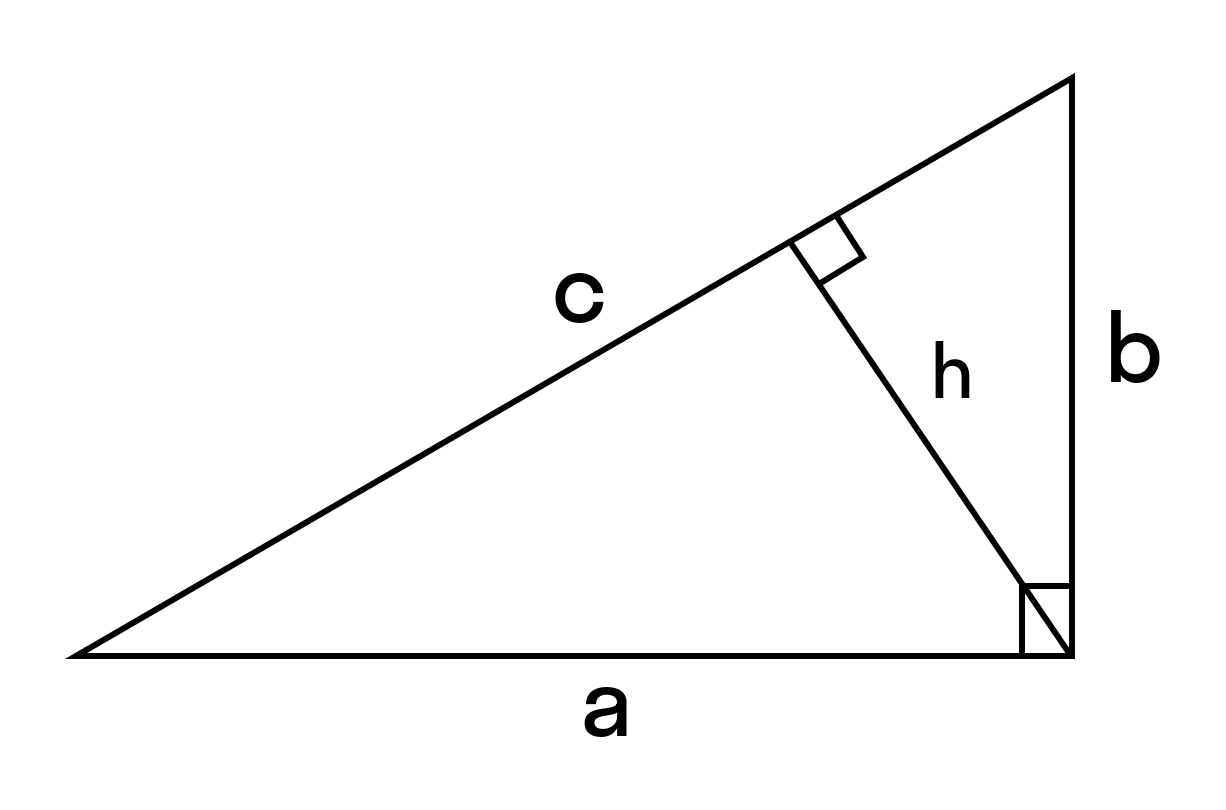
Так как высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу:
площадь прямоугольного треугольника
через проекции его
катетов на гипотенузу:
II. Площадь треугольника равна половине произведения его сторон на синус угла между ними:
Для прямоугольного треугольника эту формулу можно записать как
Нахождение площади прямоугольного треугольника по формуле Герона либо через радиус вписанной или описанной окружности также возможно, но нецелесообразно, поскольку ведет к усложнению вычислений.
Все основные формулы площади прямоугольного треугольника
1. Если известны только катеты
Формула площади треугольника через катеты ( S ) :
2. Если известны острый угол и гипотенуза или катет
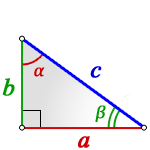
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
то справедливы следующие тождества:
3. Если известны радиус вписанной окружности и гипотенуза
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :
Площадь прямоугольного треугольника
Вы будете перенаправлены на Автор24
На этой странице вы узнаете, как вычислить площадь прямоугольного треугольника, также здесь вы найдёте онлайн-калькуляторы для вычисления площади прямоугольного треугольника по различным заданным величинам.
Прямоугольный треугольник — это треугольник, один из углов которого является прямым, при этом два другие угла — острые.
Для того чтобы воспользоваться приведёнными онлайн-калькуляторами для расчётов, введите известные величины.
Одной из самых простых формул для вычисления площади прямоугольного треугольника является формула через катеты.
Площадь прямоугольного треугольника по двум катетам
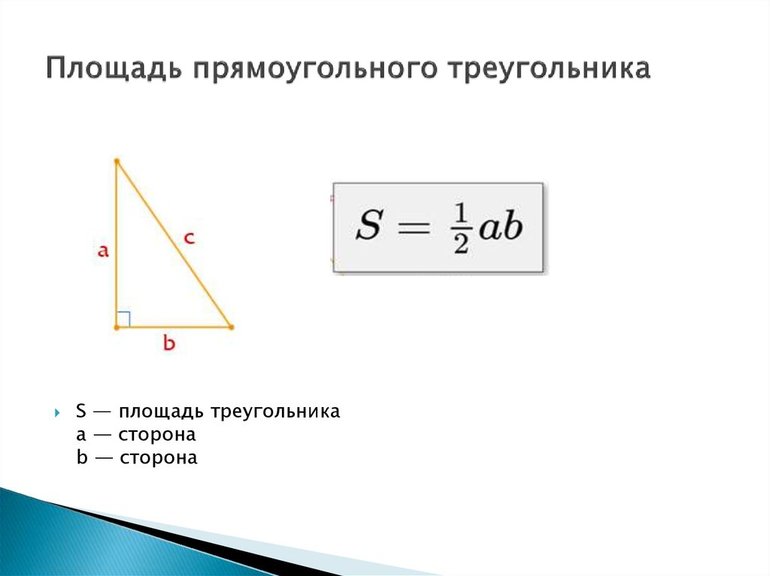
Формула площади прямоугольного треугольника по двум катетам выглядит как:
$S = \frac12 \cdot a \cdot b$, где
Задача
Решение:
Самой длинной стороной в треугольнике является гипотенуза, поэтому воспользуемся формулой вычисления площади через катеты:
$S = \frac12 \cdot a \cdot b = \frac12 \cdot 3 \cdot 4 = 6$.
Также площадь прямоугольного треугольника можно вычислить если известна гипотенуза и угол между гипотенузой и одним из катетов.
Площадь прямоугольного треугольника по гипотенузе и углу
Площадь прямоугольного треугольника через гипотенузу можно найти по формуле для площади треугольника через 2 стороны и синус угла между ними:
$S = \frac12 \cdot a \cdot c \cdot \sin (α)$ (1).
Для начала необходимо найти одну из его сторон.
Для этого вспомним определение косинуса:
$a = c \cdot \cos (α)$.
$S = \frac12 c^2 \cdot \cos (α) \cdot \sin (α)$, здесь
Задача
Решение:
$a = c \cdot \cos (30°) ≈ 7 \cdot 0.866 ≈ 6.06$
Подставим полученное значение для вычисления площади треугольника через синус угла:
$S = \frac12 \cdot a \cdot c \cdot \sin (α) = \frac12 \cdot 6.06 \cdot 7 \cdot 0.5 = 10.605$.
Другим способом вычисления площади прямого треугольника является вычисление через формулу Герона.
Площадь прямоугольного треугольника по формуле Герона
Рассчитать площадь прямоугольного треугольника по формуле Герона можно следующим образом:
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Площадь прямоугольного треугольника
Прямоугольным треугольником называется треугольник, у которого один из углов равняется 90°. Его площадь можно найти, если известны два катета. Можно, конечно, пойти и длинным путем – найти гипотенузу и просчитать площадь по формуле Герона, но в большинстве случаев это только займет лишнее время. Именно поэтому формула площади прямоугольного треугольника выглядит так:
Площадь прямоугольного треугольника равняется половине произведения катетов.
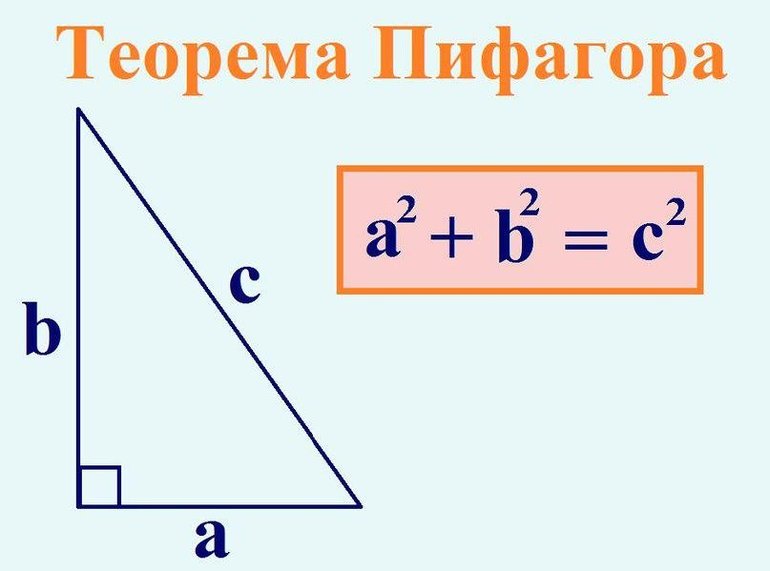
Также в прямоугольном треугольнике применяется теорема Пифагора. – сумма квадратов двух катетов равняется квадрату гипотенузы.
Формула площади равнобедренного прямоугольного треугольника вычисляется также как и обычного прямоугольного треугольника.
Формула площади прямоугольного треугольника по гипотенузе может использоваться, если в условии дан один катет. Из теоремы Пифагора находим длину неизвестного катета. К примеру, дана гипотенуза c и катет a, катет b будет равен:
Далее вычисляем площадь по обычной формуле. Пример расчета формулы площади прямоугольного треугольника по гипотенузе идентичен описанному выше.
Так как мы находили стороны, то знак минус убираем.
Получается, что катет a = 40 см, а b = 9 см.
Площадь прямоугольного треугольника – как определить по формуле
Площадь прямоугольного треугольника – это далеко не самая сложная тема по математике, но все же она нередко вызывает вопросы у школьников. В этой статье мы расскажем об основных способах нахождения этой величины и подберем формулы, подходящие для решения заданий из школьной программы.
Математические определения
Прямоугольный треугольник – это тот, один из углов которого является прямым, то есть равен 90 градусам. Чтобы научиться находить площадь этой фигуры, сначала нужно запомнить следующие определения:
Формулы определения площади прямоугольного треугольника
Для нахождения площади этого треугольника можно использовать разные формулы в зависимости от того, какие данные даются в задаче.
Задачи для тренировки
Теперь нужно закрепить знания и научиться находить площадь прямоугольного треугольника по формулам, которые мы рассмотрели ранее. Для этого рассмотрим две типовые задачи:
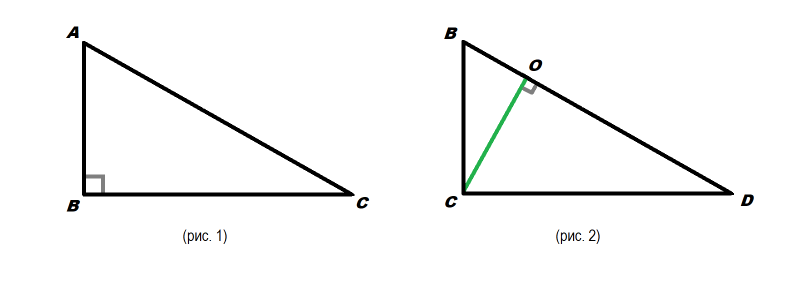
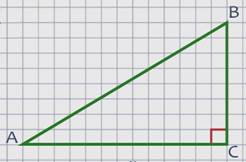
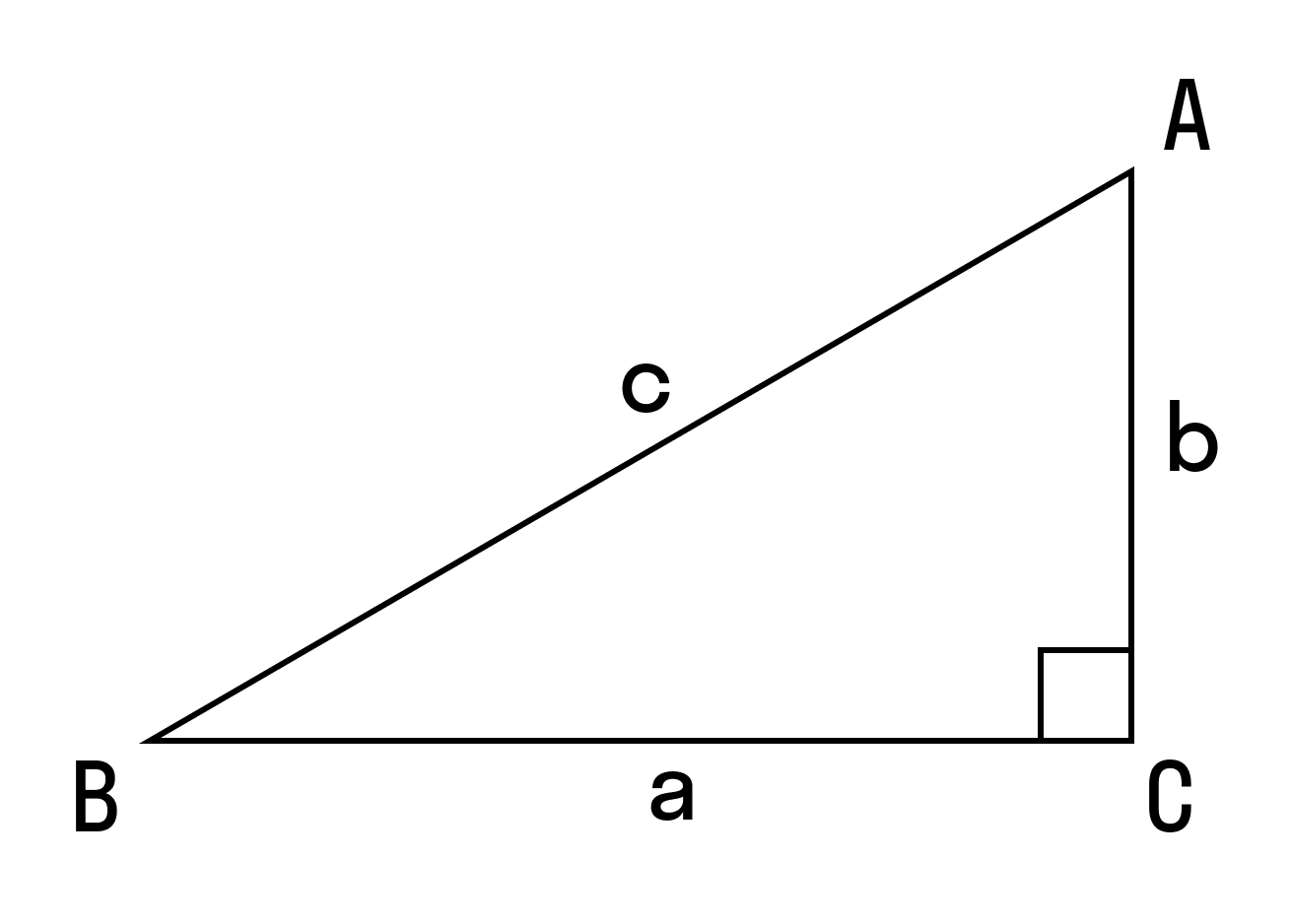
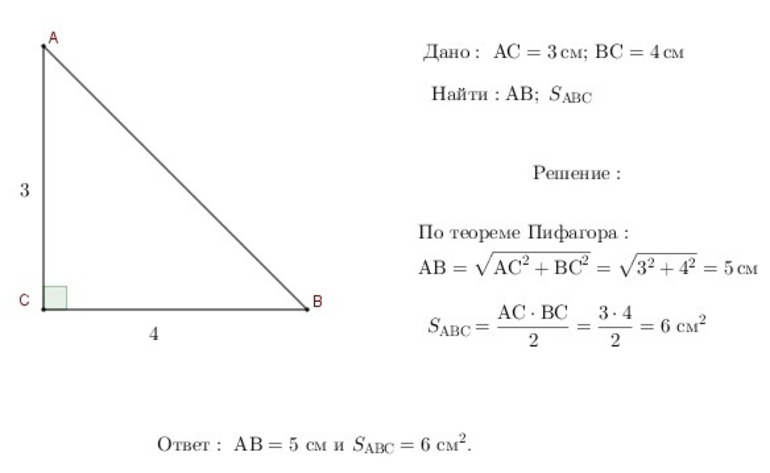
Задача №1 (рисунок 1). Известно, что у треугольника ABC c ∠ABC = 90° сторона AB = 3 см, а BC = 6 см. Нужно найти площадь этой фигуры.
Нам нужно воспользоваться первой из ранее рассмотренных формул и найти половину от произведения катетов: (3*6)/2 = 9 см².
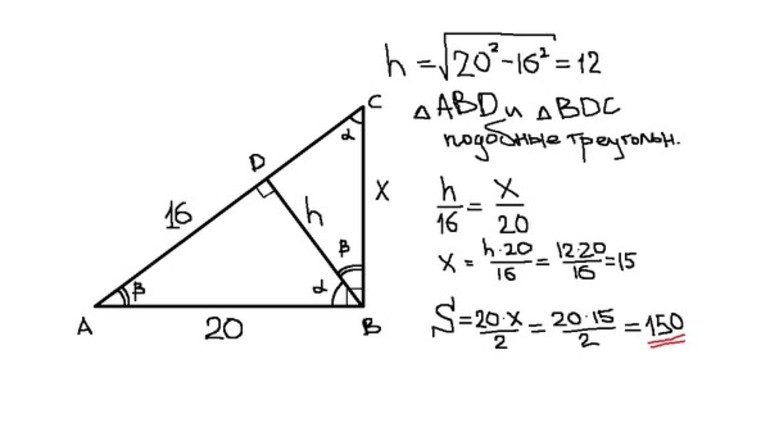
Задача №2 (рисунок 2). Из прямого угла в треугольнике BCD проведена высота BO = 4 дм, а сторона BD = 8 дм. Чему будет равна S?
В этом случае воспользуемся второй по счету формулой, и с ее помощью найдем половину от произведения гипотенузы и высоты: (4*8)/2 = 16 дм².
Курсы по математике
Тема, рассмотренная в данной статье, является лишь одной из многих, которые детям предстоит освоить. Математика включает в себя широкий комплекс знаний, и чтобы хорошо знать этот предмет, школьникам нужно не только последовательно проходить материал, но и дополнительно развивать свои математические способности.
Помочь справиться с этой задачей может курс по математике для учеников 1-4 классов Амаматика от академии развития интеллекта AMAkids. На занятиях ребята не только расширят свои математические знания, но и познакомятся со смежными областями математики. Благодаря использованию развивающих игр и различных интерактивных материалов дети с интересом будут развивать свои способности – логику, мышление, креативность.
Запишитесь на курс Амаматика и начните развивать навыки ребенка уже сейчас!
Калькулятор площади прямоугольного треугольника
Прямоугольный треугольник встречается в реальности практически на каждом углу. Знание о свойствах данной фигуры, а также умение вычислять ее площадь, несомненно пригодится вам не только для решения задач по геометрии, но и в жизненных ситуациях.
Геометрия треугольника
В элементарной геометрии прямоугольный треугольник — это фигура, которая состоит из трех соединенных отрезков, формирующих три угла (два острых и один прямой). Прямоугольный треугольник — оригинальная фигура, характеризующаяся рядом важных свойств, которые составляют фундамент тригонометрии. В отличие от обычного треугольника стороны прямоугольной фигуры имеют собственные названия:
Именно соотношение катетов и гипотенузы составляет основу тригонометрии: синусы, тангенсы и секансы определяются как отношение сторон прямоугольного треугольника.
Прямоугольный треугольник в реальности
Данная фигура получила широкое распространение в реальности. Треугольники находят применение в проектировании и технике, поэтому расчет площади фигуры приходится выполнять инженерам, архитекторам и проектировщикам. Форму треугольника имеют основания тетраэдров или призм — трехмерных фигур, которые легко встретить в повседневности. Кроме того, угольник — наиболее простое представление «плоского» прямоугольного треугольника в реальности. Угольник — это слесарный, чертежный, строительный и столярный инструмент, который используется для построения углов как школьниками, так и инженерами.
Площадь треугольника
Площадь геометрической фигуры — это количественная оценка того, какая часть плоскости ограничена сторонами треугольника. Площадь обычного треугольника можно найти пятью способами, используя формулу Герона или оперируя при расчетах такими переменными, как основание, сторона, угол и радиус вписанной или описанной окружности. Самая простая формула площади выражается как:
где a – сторона треугольника, h – его высота.
Формула для вычисления площади прямоугольного треугольника еще проще:
где a и b – катеты.
Работая с нашим онлайн-калькулятор, вы можете вычислить площадь треугольника, используя три пары параметров:
В задачах или бытовых ситуациях вам будут даны разные комбинации переменных, поэтому такая форма калькулятора позволяет вычислить площадь треугольника несколькими способами. Рассмотрим пару примеров.
Примеры из реальной жизни
Керамическая плитка
Допустим, вы хотите выполнить облицовку стен кухни керамической плиткой, которая имеет форму прямоугольного треугольника. Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:
Это означает, что площадь одного элемента составляет 24,5 квадратных сантиметра или 0,01805 квадратных метра. Зная эти параметры, вы можете подсчитать, что для отделки 7 квадратных метров стены вам понадобится 7/0,01805 = 387 элементов облицовочной плитки.
Школьная задача
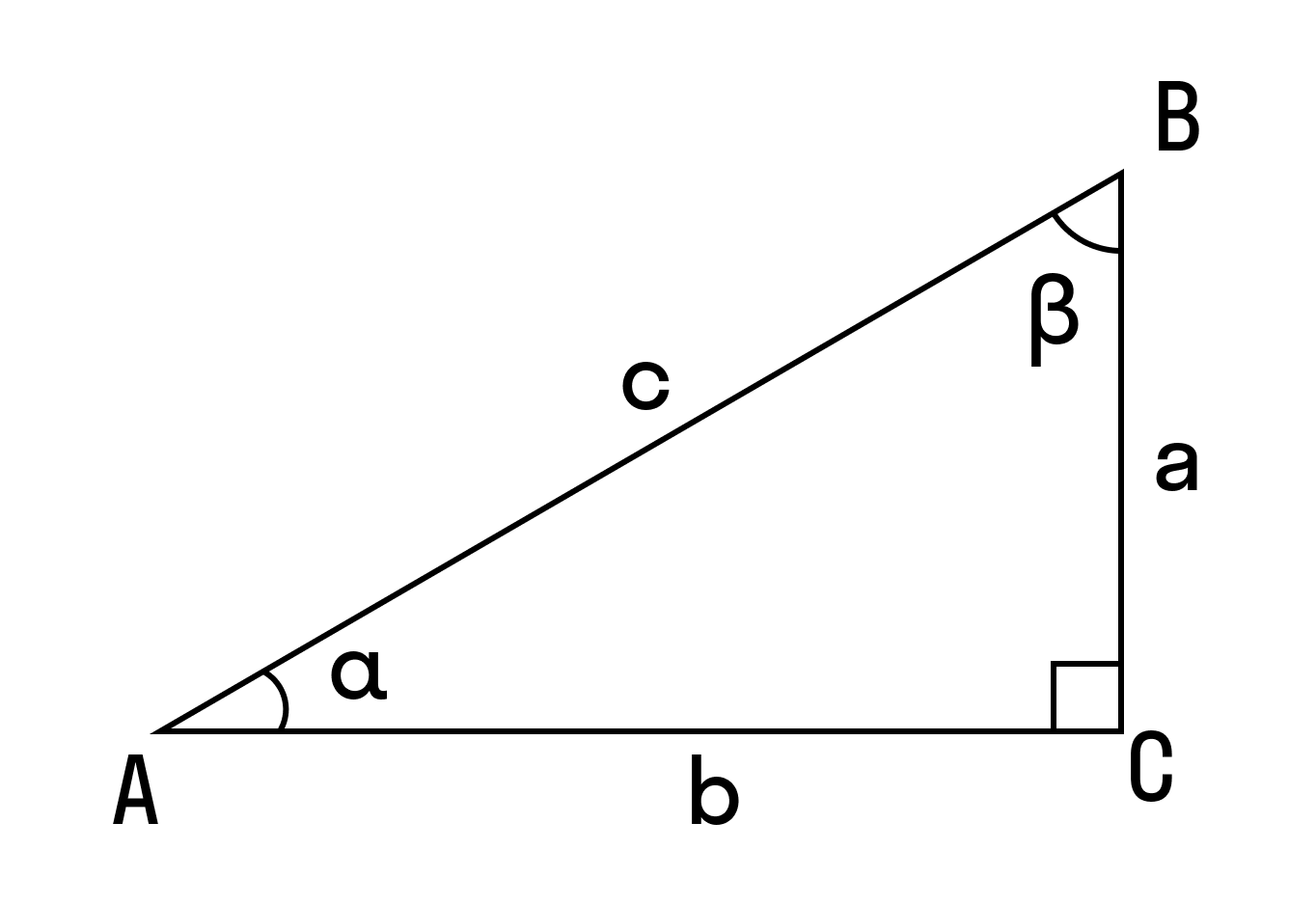
Пусть в школьной задаче по геометрии требуется найти площадь прямоугольного треугольника, зная только то, что сторона одного катета равна 5 см, а величина противолежащего угла составляет 30 градусов. Наш онлайн-калькулятор сопровождается иллюстрацией, на которой указаны стороны и углы прямоугольного треугольника. Если сторона a = 5 см, то ее противолежащий угол — это угол альфа, равный 30 градусов. Введите эти данные в форму калькулятора и получите результат:
Таким образом, калькулятор не только вычисляет площадь заданного треугольника, но и определяет длину прилежащего катета и гипотенузы, а также величину второго угла.
Заключение
Прямоугольные треугольники встречаются в нашей жизни буквально на каждом углу. Определение площади таких фигур пригодится вам не только при решении школьных заданий по геометрии, но и повседневной и профессиональной деятельности.
Как найти площадь прямоугольного треугольника?
Хотелось бы собрать разные формулы в зависимости от того, какие элементы треугольника заданы.
площадь прямоугольного треугольника можно вычислить:
s=a x b/2,
s=a2/tg c
-если задан катет и прилежащий к нему угол:
-если задана высота и один из катетов:
s=d2(1/sin c + 1/sin ( 90-c )=d2 ( 1/ sin c + 1/cos c ),
Наиболее распространенная формула для вычисления площади прямоугольного треугольника выводится очень просто.
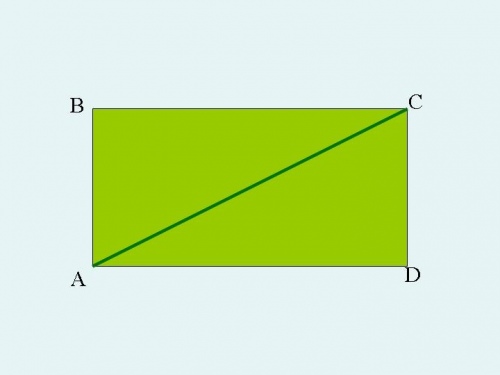
Если взять прямоугольник и провести в нём диагональ, то получим 2 равных прямоугольных треугольника.
Площадь прямоугольника равна произведению сторон: S = a *b.
Если дана гипотенуза и один из катетов, то нужно с помощью теоремы Пифагора найти другой катет.
Например, гипотенуза c = 10 см. и катет a = 6 см.
Следовательно, S = 0,5 * 6 * 8 = 24 см.
Также есть формулы, позволяющие найти площадь прямоугольного треугольника через известные углы.
Если известна сторона и один из острых углов, то в первую очередь определяем неизвестный угол.
Площадь прямоугольного треугольника в этом случае будет определяться по формуле:
Осталось лишь подставить известные значения в эту формулу и посчитать площадь.
Площадь прямоугольного треугольника как вычислить
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке научимся находить площадь прямоугольного треугольника.
Давайте отправимся в страну «Геометрия» в город треугольников. Здесь всё треугольное: и дома, и деревья, и даже жители. На первый взгляд, эти жители все очень похожи: у них по три угла, три стороны и три вершины. Но при этом все они отличаются друг от друга. Давайте рассмотрим некоторые из них:
Этот треугольник тупоугольный,
в нем содержится тупой угол.
Это равносторонний треугольник –
у него все стороны равны.
А вот треугольник, у которого равны две стороны.
Его называют равнобедренным.
А это треугольник,
в котором угол С – прямой.
Такой треугольник называют прямоугольным.
С прямоугольным треугольником мы познакомимся поближе.
Но сначала давайте решим задачу.
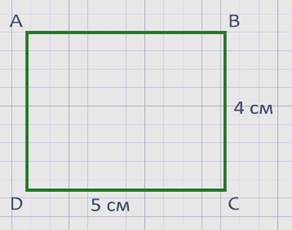
Дан прямоугольник АВСD со сторонами 5 см и
4 см. Нужно найти площадь этого прямоугольника.
Вспомним формулу нахождения площади прямоугольника.
Формула – это верное равенство, устанавливающее взаимосвязь между величинами.
Чтобы найти площадь прямоугольника, нужно длину умножить на ширину (S = a× b). Значит, S = 5 × 4 =20см2.
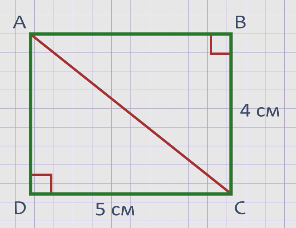
Теперь возьмём наш прямоугольник и проведём в нём диагональ АС.
Диагональю прямоугольника называется любой отрезок, соединяющий две вершины противоположных углов прямоугольника.
Мы видим, что диагональ разделила наш прямоугольник на два одинаковых треугольника. Оба эти треугольника прямоугольные, так как каждый из них содержит прямой угол.
Теперь можно легко найти площадь каждого из этих треугольников. Нужно просто площадь прямоугольника разделить пополам. Значит, площадь каждого из этих треугольников будет равна
S∆ = 20 : 2 = 10 см2.
У нас получилось, что площадь прямоугольного треугольника равна половине площади прямоугольника.
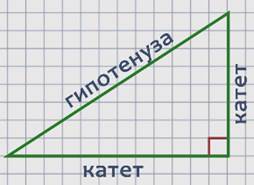
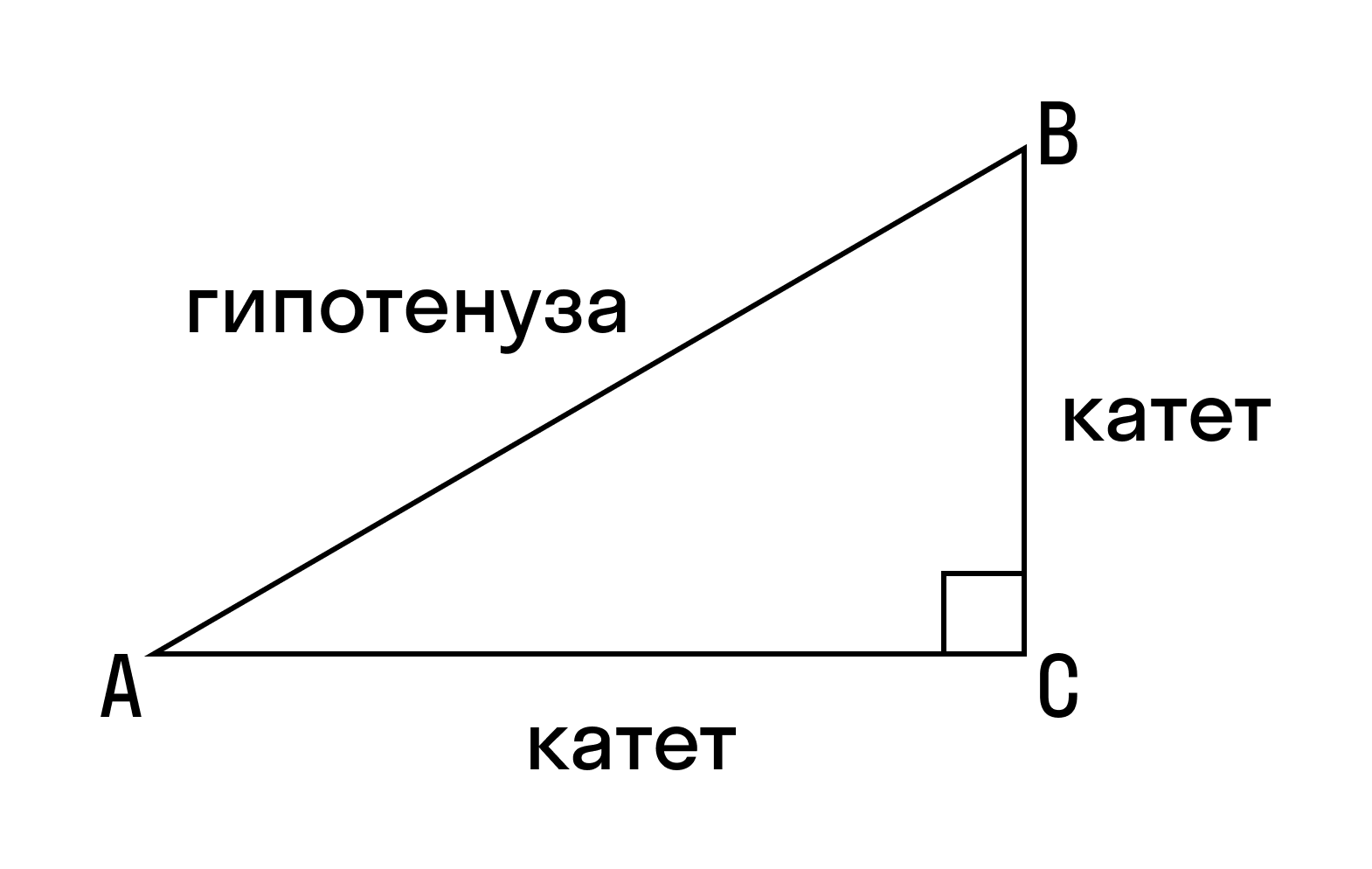
Стороны прямоугольного треугольника имеют свои названия, давайте с ними познакомимся.
Стороны прямоугольного треугольника, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла, называется гипотенузой.
Чтобы легче было запомнить, можно выучить небольшие стихи о катетах и гипотенузе.
Мы два брата-стороны, катетами названы.
Болтаем мы о том, о сём, сходясь в вершине в углу прямом.
Гипотенуза – я, особый элемент, длинней меня сторон здесь просто нет.
Меня найти нетрудно, право слово,
Лежу напротив я угла прямого.
Теперь выведем правило нахождения площади прямоугольного треугольника, зная, как называются его стороны.
Площадь прямоугольного треугольника равна половине произведения его катетов.
где a и b – катеты прямоугольного треугольника.
Рассмотрим нахождение площади прямоугольного треугольника на примере.
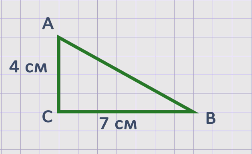
Нам дан треугольник АВС.
Сначала измерим его катеты.
Катет АС = 4 см, катет СВ = 7 см.
Вспомним правило нахождения площади прямоугольного треугольника.
Площадь прямоугольного треугольника равна половине произведения его катетов.
Эту формулу необходимо запомнить.
Подставим в неё вместо букв значения.
S∆ = (4 × 7) : 2 = 28 : 2 = 14 см2.
Используя данные знания, Вы сможете вычислять площадь и других фигур, разделив их на знакомые фигуры, площадь которых Вы уже умеете вычислять.
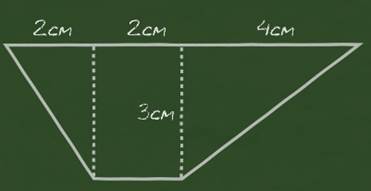
Давайте найдём площадь трапеции.
Для этого мы разделим её вертикальными линиями на прямоугольник и два прямоугольных треугольника, как показано на рисунке.
Найдём сначала площадь прямоугольника. Его длина – 3 см, ширина – 2 см.
Вспомним формулу нахождения площади прямоугольника.
Выполняем первое действие:
1) 3 × 2 = 6 см2 – S прямоугольника.
Теперь находим площади треугольников. Вспомним формулу нахождения площади прямоугольного треугольника.
Площадь прямоугольного треугольника равна половине произведения его катетов.
где a и b – катеты прямоугольного треугольника
Найдём площадь левого треугольника, его катеты 2 см и 3 см.
2) (2 × 3) : 2 = 3 см2 – площадь левого треугольника.
Найдём площадь правого треугольника. Его катеты 3 см и 4 см.
3) (3 × 4) : 2 = 6 см2 – площадь правого треугольника.
Чтобы узнать площадь всей фигуры, надо сложить площади этих трёх фигур.
4) 6 + 3 + 6 = 15 см2 – площадь трапеции.
Ответ: площадь трапеции равна 15 см2.
Подведем итоги нашего урока:
Чтобы вычислить площадь прямоугольного треугольника, необходимо:
1.Найти у треугольника катеты (это стороны, образующие прямой угол).
2.Определить их длину.
3.Вспомнить формулу нахождения площади прямоугольного треугольника. Площадь прямоугольного треугольника равна половине произведения его катетов.
4.Подставить в формулу вместо букв их значения.
5.Вычислить значение получившегося выражения, т.е. площади.
Два способа найти площадь прямоугольного
Все основные формулы площади прямоугольного треугольника
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется — гипотенуза
1. Если известны только катеты
Формула площади треугольника через катеты ( S ) :
2. Если известны острый угол и гипотенуза или катет
c — гипотенуза
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если
то справедливы следующие тождества:
3. Если известны радиус вписанной окружности и гипотенуза
c — гипотенуза
r — радиус вписанной окружности
О — центр вписанной окружности
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :
Площадь прямоугольного треугольника
О чем эта статья:
площадь, 8 класс
Основные определения
Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть равен 90˚.
Гипотенуза — это сторона, противолежащая прямому углу.
Катеты — это стороны, прилежащие к прямому углу.
Чтобы найти площадь прямоугольного треугольника, можно применить любую формулу нахождения площади треугольника — их несколько.
Формула для нахождения площади прямоугольного треугольника через катеты
Чтобы найти площадь, нужно вывести формулу:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию.
Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.
Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.
S = 1/2 (a × b), где a и b — катеты
Формула для нахождения площади прямоугольного треугольника через гипотенузу
Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе.
где с — гипотенуза,
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через гипотенузу.
Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол
α, β — острые углы
Формулы нахождения площади прямоугольного треугольника через катет и угол
α, β — острые углы
Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
Радиус вписанной окружности выражается через катеты и гипотенузу вот так:
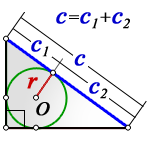
S прямоугольного треугольника = r (r + c) = c1 × c2
r — радиус вписанной окружности
C1 и С2 — отрезки, полученные делением гипотенузы на две части точкой касания с окружностью
Как найти площадь прямоугольника – 9 способов с формулами и примерами
Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
По стороне и диаметру описанной окружности
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.
По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
По стороне и периметру – 2 способ
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
По радиусу описанной окружности и углу между диагоналями – второй способ
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
Разные способы © 2022
Внимание! Информация, опубликованная на сайте, носит исключительно ознакомительный характер и не является рекомендацией к применению.
Формула площади прямоугольного треугольника
Средняя оценка: 4.5
Всего получено оценок: 252.
Средняя оценка: 4.5
Всего получено оценок: 252.
Площадь прямоугольного треугольника можно найти несколькими способами. Прямой угол в составе любой фигуры добавляет ей свойств и это можно использовать для правильного и быстрого решения задач.
Прямоугольный треугольник
Для начала обсудим сам прямоугольный треугольник, его особенности и свойства. Прямоугольный треугольник это треугольник, в составе которого есть угол.
Прямоугольный треугольник не может быть тупоугольным, потому что тогда сумма углов треугольника превысит 180 градусов, а это невозможно.
В прямоугольном треугольнике две из трех высот совпадают со сторонами – катетами. По этой же причине точка пересечения высот прямоугольного треугольника совпадает с вершиной при прямом угле.
Рис. 1. Все высоты прямоугольного треугольника.
Эта же точка будет центром описанной окружности.
Площадь треугольника
Площадь треугольника обычно находится по стандартной формуле, как половина произведения основания на высоту, проведенную к этому основанию.
Можно найти площадь как половину произведения сторон на синус угла между ними:
Существуют усложненные формулы нахождения площади, но они используются крайне редко.
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника находится по тем же формулам, но в некоторых случаях эти формулы можно упростить.
Например, можно воспользоваться тем, что высоты в прямоугольном треугольнике совпадают с катетами. Тогда стандартная формула превратится в следующую:
$S=<1\over2>*a*b$, где а и b это катеты прямоугольного треугольника.
Это одна из самых простых формул площади прямоугольного треугольника. Попробуем преобразовать вторую формулу.
Если вспомнить, что синус угла это отношение противолежащего катета к гипотенузе. В нашем случае, противолежащий катет обозначим за букву f, потому как а это прилежащий катет, а острый угол может быть заключен только между катетом и гипотенузой. Значит b это гипотенуза.
Рис. 2. Рисунок к выводу.
Значит, первый вывод мы осуществили правильно, а у прямоугольного треугольника есть только одна специальная формула для нахождения площади. Если она не подойдет можно воспользоваться общими формулами. Это и есть два возможных пути расчета площади.
Например, если по условию задачи известна гипотенуза, то можно попробовать найти высоту, падающую на гипотенузу и определить площадь по общей формуле. По тому же принципу можно найти площадь через синус, если известны гипотенузы и катет.
Рис. 3. Высота, проведенная к гипотенузе.
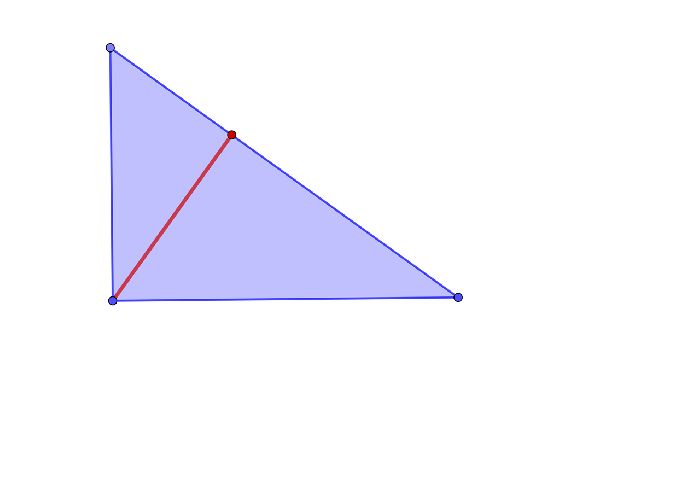
Главное помнить, что у любой задачи всегда есть 3 решения и решать каждую наиболее удобным способом.
Что мы узнали?
Мы поговорили о прямоугольных треугольниках и вывели формулу площади прямоугольного треугольника через катеты. Обсудили общие формулы площади треугольников и сказали, что каждая из этих формул подойдет для решения прямоугольного треугольника.
Площадь прямоугольного треугольника
Средняя оценка: 4.2
Всего получено оценок: 238.
Средняя оценка: 4.2
Всего получено оценок: 238.
В 7 классе изучают различные виды треугольников. Сегодня мы узнаем, как измерять площадь прямоугольного треугольника, а также общие характеристики этой фигуры.
Определение понятия
Известно, что треугольник состоит из трех точек и такого же количества отрезков. Тогда часть плоскости, которую ограничивают эти линии, и будет площадью рассматриваемой фигуры.
В общем случае для нахождения численной характеристики любой плоской фигуры используются такие параметры, как значения сторон и углов. Иногда приходится совершать дополнительные построения.
Рис. 1. Общий вид прямоугольного треугольника.
Проще всего определить площадь прямоугольного треугольника через катеты. Но это не всегда возможно, поэтому иногда приходится пользоваться другими формулами.
Характеристики понятия
В прямоугольном треугольнике один из углов равняется 90 градусов. Поэтому при нахождении его площади чаще всего не нужно находить высоту, две из трех высот треугольника совпадает с катетами.
Достаточно найти произведение числовых значений катетов этой геометрической фигуры, и потом разделить результат на два. Таким образом, получаем общую формулу для определения площади прямоугольного треугольника через катеты:
Рис. 2. Площадь прямоугольного треугольника.
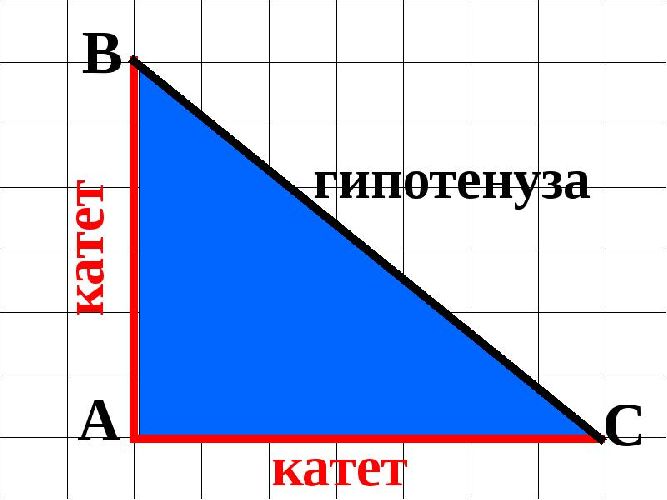
Частные случаи
Для получения правильного результата при определении площади прямоугольного треугольника можно использовать другие формулы.
Рис. 3. Высота в прямоугольном треугольнике.
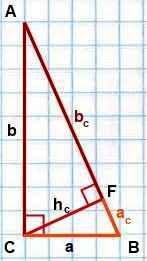
Так площадь прямоугольного треугольника можно найти через гипотенузу и катет, используя острый угол между ними:
Эту формулу так же называют формулой через гипотенузу и катет. Помимо нее может быть использована любая формула, применимая к произвольному треугольнику.
Решение задач
Для нахождения площади прямоугольного треугольника могут понадобиться дополнительные построения. В некоторых случаях придется опускать высоту на гипотенузу, чтобы получить высоту или два пропорциональных отрезка.
Хотя существуют такие задачи, в условиях которых указаны числовые значения отрезков соединяющих вершину и основание. Это может быть медиана или биссектриса. Конечно, лучше упрощать задачу, используя простые формулы, в зависимости от требуемого результата.
Любую геометрическую фигуру можно разбить на треугольники. Поэтому через формулу площади треугольника можно найти площадь сложной фигуры.
Площадь прямоугольного треугольника можно находить, пользуясь формулой Герона, радиусом вписанной или описанной окружности.
Что мы узнали?
Площадь произвольного треугольника обычно представляет собой численную характеристику плоской геометрической фигуры. Определить площадь можно несколькими способами, воспользовавшись соответствующими формулами. Однако когда речь идет о прямоугольном треугольнике, задача упрощается, потому что две из трех высот треугольника совпадает с катетами. Поэтому достаточно подставить в формулу значения катетов.
Свойства треугольника
Пожалуй, в жизни любой человек сталкивается с треугольниками. Они бывают разными: остроугольными, тупоугольными, прямоугольными, равнобедренными и равносторонними. Но всех их объединяет один признак — существование трёх углов. Точное определение фигуре дали ещё в Древней Греции. Евклид утверждал, что этот объект состоит из трёх точек, расположенных на разных прямых, и трёх замкнутых линий, поочерёдно соединяющих эти точки.
Три точки, ограничивающие отрезки, называют вершинами, а линии, соединяющие их, — сторонами. Внутреннюю плоскость, заключённую в линии, называют площадью. Так как отрезки фигуры образуют три угла, то объект относится к классу многоугольников. Замкнутая прямая, соединяющая вершину с серединой противолежащей стороны, носит имя медиана. Всего их может быть три штуки, пересекаться они могут в одной точке, которую называют центроидом. Он является центром тяжести.
Если из угла провести перпендикуляр к противолежащей стороне, то полученная линия будет высотой. Линия, опущенная к стороне напротив угла и разделяющая его пополам, называется биссектрисой. В любой треугольник можно вписать окружность. Она будет единственной, так как должна касаться всех трёх сторон. Центр круга всегда будет совпадать с местом пересечения биссектрис.
Разделение треугольников происходит по размерам углов и сторон. Например, у равносторонней фигуры любой из трёх углов равен 60 градусам, у равнобедренной — две стороны и два угла равны. Для любого треугольника справедливо утверждать следующее:
В элементарной математике часто используют правила, называемые признаками подобия и равенства. Так, при сравнении две фигуры будут равными, если длины их сторон совпадают. Соответственно, углы тоже станут одинаковыми или будут равными две стороны и угол между ними.
Прямоугольная фигура
Треугольник с одним прямым углом, то есть составляющим 90 градусов, называется прямоугольным. Два отрезка, примыкающие к нему, называют катетами, а прямую, соединяющую их, — гипотенузой. Из любого треугольника можно получить две прямоугольных фигуры. Для этого нужно в нём опустить высоту. Многие свойства многоугольника идентичны прямоугольной фигуре. Два равных треугольника можно объединить в прямоугольник, при этом их гипотенузы будут совпадать с диагональю.
Из теоремы Пифагора можно сделать важное следствие. Становится очевидным, что высота, опущенная из прямого угла, разделит гипотенузу на два отрезка: c1 = a2/c и c1 = b2/c. Полученные замкнутые линии являются проекциями катетов. В то же время высоту фигуры можно определить, используя следующую формулу: h = √ca + cb.
Все рассмотренные формулы и свойства помогают при нахождении площади фигуры. Но кроме них полезно знать и то, что радиус вписанной окружности в прямоугольную фигуру можно узнать, найдя разницу суммы катетов и гипотенузы, разделённую на 2, то есть r = (a + b — c) / 2.
Формулы площади
Найти площадь треугольника с прямым углом можно различными способами. Но проще всего это сделать через катеты. Выражение для нахождения параметра довольно простое: S = (a * b) / 2. Это классическая формула площади прямоугольного треугольника. Существуют и другие формулы:
Другими словами, площадь можно определить, зная значения двух катетов, длину одного из них и разворот противолежащего или прилежащего угла. Для доказательства теоремы нахождения площади понадобится изобразить фигуры с катетами b и a. Фигуру можно достроить до параллелограмма, отложив параллельные катетам прямые. Вершины полученного объекта можно обозначить буквами A, B, C, D, начиная с прямого угла треугольника и двигаясь влево.
Прямоугольник образуется двумя треугольниками, равными между собой по трём сторонам: AB = CD, AC = BD (ВС — общая сторона). Учитывая равенства, можно утверждать, что площади фигур равны друг другу. Следовательно, площадь параллелограмма можно найти через сумму площадей двух треугольников: S = Sabc + Sacd. Отсюда верным будет утверждение, что площадь начального треугольника ABC равняется половине замкнутой области прямоугольника, а та соответствует произведению сторон: S = a * b, то есть AB * BC.
Эта формула легко доказывается с учётом того, что прямоугольник является фигурой, в которую можно вписать несколько четырёхугольников. Так как общая площадь будет равняться сумме площадей внутренних фигур, то верным будет равенство: (a + b)2 = S + S + a2 + b2 = a2 + 2ab + b2 = 2S + a2 + b2. Отсюда получим, что S = a* b. Следовательно, так как площадь треугольника равняется половине площади прямоугольной фигуры, то можно утверждать, что S = (a * b)/2 = (AB * BC) / 2. Формула доказана.
Из этого правила вытекают два следствия:
Использование рассмотренных следствий помогает при решении многих геометрических задач. Они касаются не только треугольников, но и других многоугольных фигур.
Решение задач
Важно не только знать формулы для нахождения площади, но и уметь их применять на практике. Это возможно лишь с опытом, который можно получить, решая различные задания. Существуют определённые задачи, которые ученикам нужно решить самостоятельно. После успешного решения можно утверждать, что учащиеся полностью разобрались в теме, поэтому они могут переходить к следующему разделу геометрии. Вот некоторые задания, позволяющие закрепить теоретический материал:
Таким образом, площадь прямоугольной фигуры — ее численная характеристика. Определить ее можно, используя несколько способов. При этом всегда необходимо знать длину хотя бы одного из катетов. Это связанно с тем, что две из трёх высот совпадают с ним.
Как вычислить площадь прямоугольного треугольника
Площадь любого четырехугольного прямоугольника на плоскости определяется произведением его длины на ширину.
В вашем случае площадь прямоугольника ABCD вычисляется перемножением AB x BC или CD x AD.
Допустим, в полученном прямоугольнике
AB = CD = 2 см.
AD = DC = 4 см.
Перемножьте. Площадь прямоугольника составит
AB x BC = 2 х 4 = 8 (см).
Из всех разновидностей треугольников площадь прямоугольного треугольника вычисляется наиболее просто и не требует особых, замысловатых расчетов.
Так как диагональ в прямоугольнике делит его площадь ровно пополам, то изначально построенный вами треугольник АВС будет составлять как раз эту половину, и его площадь будет равна ½ площади прямоугольника ABCD.
8 : 2 = 4 (см).
Продолжая, рассуждайте так:
Стороны АВ и ВС прямоугольника ABCD одновременно являются катетами треугольника АВС.
Исходя из этого, делайте вывод.
Чтобы вычислить площадь прямоугольного треугольника, надо перемножить числовые значения его катетов и, учитывая, что площадь треугольника – это ½ площади прямоугольника с подобными сторонами, разделить результат пополам.
В результате вы получили формулу:
Sтр. = ½ AB*ВС.
Прямоугольный треугольник по своей сути является половиной прямоугольника. Его гипотенуза – это диагональ, а катеты – длина и ширина легко достраиваемого прямоугольника. Следовательно, площадь прямоугольного треугольника будет составлять ровно половину прямоугольника с подобными сторонами.
Как найти площадь прямоугольного треугольника
Треугольник – плоская геометрическая фигура с одним углом равным 90 °. При этом в геометрии очень часто требуется вычислить площадь такой фигуры. Как это сделать, мы расскажем далее.
Исходные данные, где: a и b – стороны треугольника, выходящие из прямого угла.
То есть, площадь равна половине произведения двух сторон, которые выходят из прямого угла. Конечно, существует формула Герона, используемая для вычисления площади обычного треугольника, но для определения величины необходимо знать длину трех сторон. Соответственно, вам придется рассчитать гипотенузу, а это лишнее время.
Это всем известная и исходная формула, но для этого вам придется посчитать гипотенузу по двум катетам, используя Теорему Пифагора.
В этой формуле: a, b, c – стороны треугольника, а p – полупериметр.
Если в вашей задаче не известен ни один из катетов, то воспользоваться самым простым способом вы не сможете. Для определения величины вам нужно рассчитать длину катетов. Это сделать просто по гипотенузе и косинусу прилежащего угла.
b=c×cos(α)
Узнав длину одного из катетов, по теореме Пифагора вы сможете рассчитать вторую сторону, выходящую из прямого угла.
В этой формуле c и a – гипотенуза и катет соответственно. Теперь можете рассчитать площадь по первой формуле. Точно так же можно вычислить один из катетов, имея второй и угол. В таком случае одна из искомых сторон будет равна произведению катета на тангенс угла. Существуют и другие способы вычисления площади, но зная основные теоремы и правила, вы сможете легко найти искомую величину.
Если у вас нет ни одной из сторон треугольника, а имеется лишь медиана и один из углов, то вы сможете вычислить длину сторон. Для этого используйте свойства медианы делить прямоугольный треугольник на два. Соответственно, она может выступать гипотенузой, если выходит из острого угла. Воспользуйтесь теоремой Пифагора и определите длину сторон треугольника, выходящих из прямого угла.
Как видите, зная основные формулы и Теорему Пифагора, вы сможете рассчитать площадь прямоугольного треугольника, имея лишь один из углов и длину одной из сторон.
Поделиться советом: “Как найти площадь прямоугольного треугольника”
Как найти площадь прямоугольного треугольника
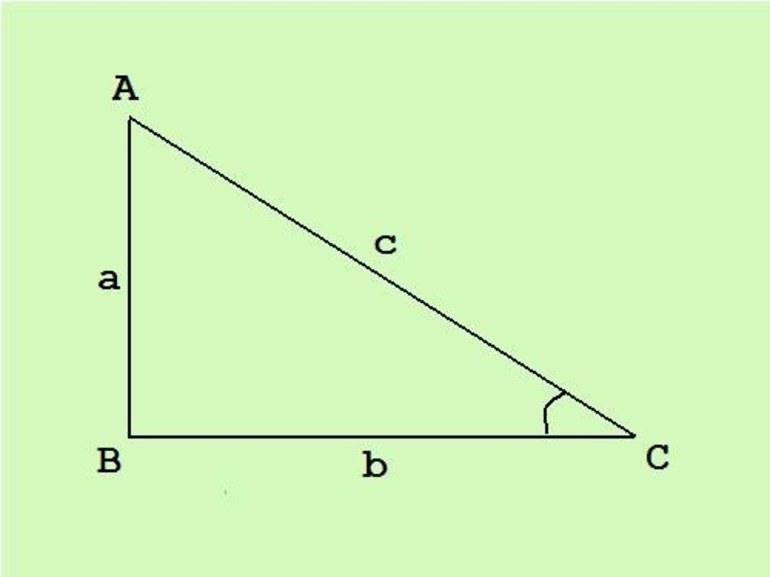
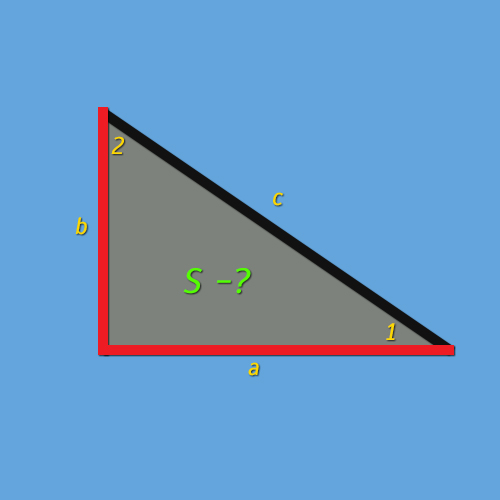
Сначала необходимо задать некоторые исходные данные. Пусть у нас имеется прямоугольный треугольник, в котором катеты обозначены буквами «a» и «b», «с» – гипотенуза. Цифрами «1» и «2» показаны углы фигуры. Искомым параметром является площадь. Далее будут рассмотрены самые типичные задачи из школьного курса по геометрии.
1. Известны значения двух катетов
В таком случае площадь прямоугольного треугольника вычисляется по формуле:
S= 0.5ab
2. Известен один катет и гипотенуза
При подобных условиях логичнее всего воспользоваться теоремой Пифагора и вышеизложенной формулой:
S = 0.5∙sqrt(c^2-a^2) ∙a,
где sqrt –квадратный корень, c^2-a^2 – подкоренное выражение, обозначающее разность квадрата гипотенузы и катета.
3. Даны значения всех сторон треугольника
Для таких задач можно использовать формулу Герона:
S = (p-a)(p-b),
где p – полупериметр, который находится по следующему выражению: p = 0.5∙ (a+b+c)
4. Известен один катет и угол
Тут стоит обратиться к тригонометрическим функциям. Например, tg(1) = 1/сtg (1) = b/a. То есть, благодаря этому соотношению можно определить значение неизвестного катета. Далее задача сводится к первому пункту.
5. Известна гипотенуза и угол
В данном случае также используются тригонометрические функции синуса и косинуса: сos(2)=1/sin(2) = b/c. Затем решение задачи сводится ко второму пункту статьи.
Площадь прямоугольного треугольника
В элементарной геометрии прямоугольным треугольником называется фигура, состоящая из трёх отрезков соединённых в точках, с углами два из которых острые, а один прямой (то есть равен 90° ). Прямоугольный треугольник характеризуется целым рядом важных свойств, многие из которых составляют основу тригонометрии (например, соотношения между его сторонами и углами). Еще со школьной скамьи все мы знаем, как вычислить площадь прямоугольного треугольника, а в повседневной жизни встречаемся с этой геометрической фигурой достаточно часто, порой даже не замечая этого. Достаточно широкое применение находит она в технике и поэтому такую задачу, как нахождение площади прямоугольного треугольника, часто приходится решать инженерам, конструкторам и архитекторам.
Зодчим определять эту величину требуется тогда, когда они проектируют здания с фронтонами, которые являются завершением фасадов и имеют треугольную форму ограниченную карнизом, а по бокам – скатами крыши. Нередко угол между скатами бывает прямой, и в таких случаях фронтон имеет форму прямоугольного треугольника. Определять его площадь требуется по той простой причине, что необходимо точно знать количество строительного материала, необходимого для его обустройства. Следует заметить, что фронтоны являются обязательными элементами малоэтажных строений (загородных домов, коттеджей, дач).
Нахождение площади прямоугольного треугольника
Формула расчёта площади прямоугольного треугольника
S – площадь прямоугольного треугольника
Форму прямоугольного треугольника имеют многие детали, из которых изготавливается современная мебель. Как известно, для того чтобы наиболее рационально использовать площадь помещений, все элементы обстановки должны размещаться в ней оптимальным образом. С пользой задействовать такие зоны, как углы, можно с помощью столов треугольной формы, столешницы которых в большинстве случаев представляют собой прямоугольные треугольники с катетами, вплотную прилегающими к стенам. При проектировании и расчете этих элементов конструкторы мебельного производства применяют формулу, по которой нахождение площади прямоугольного треугольника осуществляется на основе длины его сторон. Кроме того, им нередко приходится разрабатывать конструкции столиков, крепящихся непосредственно к стенам, в состав которых входят опорные элементы, также представляющие собой прямоугольные треугольники.
Строителям, занимающимся облицовочными работами, нередко в своей профессиональной деятельности приходится использовать керамическую плитку, имеющую форму прямоугольного треугольника с катетами одинаковой или различной длины. Им также приходится определять площадь этих элементов для того, чтобы выяснить необходимое их количество.
Форму прямоугольного треугольника имеет и такой важный и необходимый измерительный инструмент, как угольник. С его помощью производится построение и контроль прямых углов, а используется он очень широко и многими: от обычных школьников на уроках геометрии до конструкторов суперсовременной техники.
Быстро найти формулу для расчета онлайн.
1. Если известны только катеты
Формула площади треугольника через катеты ( S ) :
2. Если известны острый угол и гипотенуза или катет
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
то справедливы следующие тождества:
3. Если известны радиус вписанной окружности и гипотенуза
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :
Как найти площадь прямоугольного треугольника
Здравствуйте!
Подскажите, как можно найти площадь прямоугольного треугольника?
Спасибо!
Прямоугольный треугольник называется так именно из-за того, что один из его углов — прямой, то есть равен 90 градусов.
Площадь прямоугольного треугольника можно найти несколькими способами.
1-й способ. Известны длины двух катетов.
Если известны два катета прямоугольного треугольника, то, воспользовавшись формулой
можно вычислить его площадь.
Другими словами площадь прямоугольного треугольника равна половине произведения его катетов.
Пример 1.
У прямоугольного треугольника катеты равны 13 см и 29 см. вычислить его площадь.
Решение.
Подставим данные в формулу и вычислить площадь треугольника:
(кв. см)
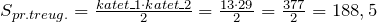
Ответ.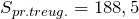 
(кв. см).
2-й способ. Известны длины катета и гипотенузы.
Для вычисления площади прямоугольного треугольника нужно знать длины обоих катетов. По известной гипотенузе с помощью теоремы Пифагора можно найти второй катет и воспользоваться формулой площади.
Согласно теореме Пифагора:
Пример 2.
Гипотенуза у прямоугольного треугольника равна 23 см, а катет — 11 см. Найдем площадь этого треугольника.
Решение.
Согласно теореме Пифагора:
(см).
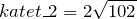
Далее используем формулу площади:
(кв. см).
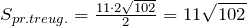
Ответ.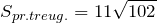 
(кв. см).
Как найти площадь прямоугольного треугольника все способы
Найти площадь прямоугольного треугольника
Онлайн калькулятор
Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
Найти площадь прямоугольного треугольника по двум катетам
Теория
Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?
Формула
Пример
К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:
S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²
Найти площадь прямоугольного треугольника по катету и гипотенузе
Теория
Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?
Формула
S = ½ ⋅ a ⋅ √ c² — a² = ½ ⋅ b ⋅ √ c² — b²
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:
S = 2 ⋅ √ 5² — 2² / 2 = √ 25 — 4 ≈ 4.58 см²
Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
То есть к катету a прилежащий ∠β, а к катету b — ∠α
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:
S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²
Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
То есть к катету a противолежащий ∠α, а к катету b — ∠β
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(90 — α) = ½ ⋅ b² ⋅ tg(90 — β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:
S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²
Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
Теория
Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?
Формула
S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:
S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²
Все основные формулы площади прямоугольного треугольника
Прямоугольный треугольник, так же как и любой другой треугольник, имеет три стороны и три угла. Разница только в том, что один угол прямой, т. е. 90 градусов и два остальных, острых угла в сумме составляют, тоже 90 градусов.
Две стороны, которые формируют прямой угол, называют катетами, а третья сторона напротив прямого угла, называется — гипотенуза
1. Если известны только катеты
Формула площади треугольника через катеты ( S ) :
2. Если известны острый угол и гипотенуза или катет
c — гипотенуза
Формулы площади прямоугольного треугольника через гипотенузу и угол ( S ) :
Формулы площади прямоугольного треугольника через катет и угол ( S ) :
Как известно, сумма острых углов в прямоугольном треугольнике равна 90 градусов, а если
то справедливы следующие тождества:
3. Если известны радиус вписанной окружности и гипотенуза
c — гипотенуза
r — радиус вписанной окружности
О — центр вписанной окружности
Формулы площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу ( S ) :
Площадь прямоугольного треугольника
О чем эта статья:
площадь, 8 класс
Основные определения
Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть равен 90˚.
Гипотенуза — это сторона, противолежащая прямому углу.
Катеты — это стороны, прилежащие к прямому углу.
Чтобы найти площадь прямоугольного треугольника, можно применить любую формулу нахождения площади треугольника — их несколько.
Формула для нахождения площади прямоугольного треугольника через катеты
Чтобы найти площадь, нужно вывести формулу:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию.
Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.
Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.
S = 1/2 (a × b), где a и b — катеты
Формула для нахождения площади прямоугольного треугольника через гипотенузу
Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе.
где с — гипотенуза,
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через гипотенузу.
Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол
α, β — острые углы
Формулы нахождения площади прямоугольного треугольника через катет и угол
α, β — острые углы
Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
Радиус вписанной окружности выражается через катеты и гипотенузу вот так:
S прямоугольного треугольника = r (r + c) = c1 × c2
r — радиус вписанной окружности
C1 и С2 — отрезки, полученные делением гипотенузы на две части точкой касания с окружностью
Как найти площадь треугольника
О чем эта статья:
Основные понятия
Треугольник — это геометрическая фигура, которая получилось из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере плоскости, ограниченной замкнутой геометрической фигурой.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Общая формула
1. Площадь треугольника через две стороны и угол между ними.
2. Площадь треугольника через основание и высоту.
S = 0,5 * a * h, где a — основание, h — высота.
3. Площадь треугольника через описанную окружность и стороны.
S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны.
S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.
Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:
S = r * p, где p — полупериметр.
5. Площадь треугольника по стороне и двум прилежащим углам.
S = a 2 : 2 * (sin(α)⋅sin(β)) : sin(180 — (α + β)), где a — сторона, α и β — прилежащие углы, γ — противолежащий угол.
6. Формула Герона для вычисления площади треугольника.
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
S = √ p * (p − a) * (p − b) * (p − c), где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам.
S = 0,5 * a * b, где a, b — стороны.
Площадь треугольника по гипотенузе и острому углу.
S = 0,25 * c 2 * sin(2α), где c — гипотенуза, α — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу.
S = 0,5 * a 2 * tg(α), где a — катет, α — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и по радиусу вписанной окружности.
S = r * (r + c), где c — гипотенуза, r — радиус вписанной окружности.
Площадь треугольника вписанного в окружность.
Площадь прямого треугольника по формуле Герона.
S = (p − a) * (p − b), где a, b — катеты, p — полупериметр, который рассчитывается по формуле p = (a + b + c) : 2.
Для равнобедренного треугольника
Поиск площади через основание и сторону.
Вычисление площади через основание и угол.
S = 0,5 * a * b * sin(α), где a — боковая сторона, b — основание, α — угол между основанием и стороной.
Вычисление площади через основание и высоту.
S = 0,5 * b * h, где b — основание, h — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними.
S = 0,5 * a 2 * sin(α), где a — боковая сторона, α — угол между боковыми сторонами.
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами.
S = b 2 : (4 * tgα/2), где b — основание, α — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности.
S = (3 * √ 3 * R 2 ) : 4, где R — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности.
Площадь равностороннего треугольника через сторону.
S = (√ 3 * a 2 ) : 4, где a — сторона.
Площадь равностороннего треугольника через высоту.
S = h 2 : √ 3, где h — высота.
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Разные способы © 2022
Внимание! Информация, опубликованная на сайте, носит исключительно ознакомительный характер и не является рекомендацией к применению.
Площадь прямого треугольника
Средняя оценка: 4.3
Всего получено оценок: 236.
Средняя оценка: 4.3
Всего получено оценок: 236.
Прямоугольный треугольник отличается от произвольных целым рядом параметров. Это и значение сторон, которое можно рассчитать по теореме Пифагора; возможность напрямую использовать тригонометрические функции и несколько специфичных формул, предназначенных для расчета площади именно прямоугольных треугольников. Именно об этих формулах и пойдет речь в данной статье.
Формула площади прямоугольного треугольника
В классическом случае, площадь треугольника находится как половина произведение стороны на высоту, проведенную к этой стороне.
Рис. 1. Площадь произвольного треугольника.
В прямоугольном треугольнике для двух из трех сторон высоты и сами стороны совпадают. Рассмотрим на примере.
Дан прямоугольный треугольник АВС с прямым углом при вершине В. Для катета ВС высотой будет катет АВ, а для катета АВ высотой служит сторона ВС. Только гипотенуза нуждается в дополнительных построениях для нахождения высоты.
Именно из этих особенностей и вытекает формула площади прямого треугольника.
$S= <1\over2>a*b$ где a и b это катеты треугольника. То есть значение двух сторон просто подставили в классическую формулу. В итоге получается самая простая из возможных формул для нахождения площади прямоугольного треугольника. Рассмотрим несколько неклассических ситуаций, когда значение катетов неизвестно.
Если в задаче о прямоугольном треугольнике дается значение высоты, то имеется в виду перпендикуляр, проведенный к гипотенузе.
Задача
Для каждой геометрической задачи существует, как минимум 3 решения.
Конкретно в нашем случае можно выделить два простых способа:
Рассмотрим каждый из вариантов, чтобы иметь представление о возможных путях решения подобных задач.
Обозначим треугольник АВС, проведем высоту ВН. Угол АСВ равен 60 градусов. Найдем гипотенузу. Она состоит из двух отрезков АН и НС. Найдем каждый из отрезков, сложим их и получим искомое значение.
АН найдем из прямоугольного треугольника АНВ с прямым углом у вершины Н. Сумма острых углов в прямоугольном треугольнике всегда равна 90 градусам. Значит Угол ВАС=90-60=30.
Воспользуемся тригонометрической функцией. Воспользуемся значением тангенса:
$$tg(BAC)=
Получившийся результат мы округлим до сотых. Не стоит бояться получившихся длинных дробных значений. В вычислениях они встречаются постоянно, нужно просто правильно округлять полученные значения.
По схожей схеме вычислим НС из прямоугольного треугольника ВНС.
Значение снова округлим до сотых. Два получившихся значения сложим и посчитаем значение площади.
Приведем решение через катеты и сравним результаты.
В прямоугольном треугольнике ВНС сторона ВС выступает гипотенузой. Воспользуемся значением синуса:
Значение синуса для угла в 60 градусов является табличным значением.
Подобным методом определим значение второго катета из треугольника АНВ:
Оба катета найдены, можно подсчитать значение площади:
Получившиеся значения схожи. Различие в сотых легко объясняется округлениями, которые выполнялись для удобства расчета. В подобных вычислениях расхождение в единицу считается допустимым.
Что мы узнали?
Мы досконально разобрали формулу нахождения площади прямоугольного треугольника. Показали другие варианты нахождения площади, подробно разобрали различные пути решения задач на нахождение площади прямоугольного треугольника.
Геометрия
План урока:
Площадь прямоугольного треугольника
Пусть в прямоугольном треугольнике известны два его катета. Обозначим их буквами а и b. Как тогда вычислить площадь такого треуг-ка?
Прямоугольный треугольник можно достроить до прямоугольника:
Площадь получившегося прямоугольника равна произведению чисел а и b. С другой стороны, прямоугольник состоит из двух треуг-ков площадью S, поэтому его общая площадь составляет 2S. Тогда можно записать, что
Задание. Катеты прямоугольного треугольника имеют длины 3 и 4. Определите его площадь.
Решение. Просто подставляем в формулу вместе букв a и b числа 3 и 4:
Задание. Площадь прямоугольного треугольника равна 100, а один катет больше другого вдвое. Найдите оба катета.
Решение. Пусть меньший катет равен х, тогда больший катет будет равен 2х. Выразим площадь прямоугольного треугольника через х:
Естественно, нас интересует только положительный корень, а отрицательный можно отбросить:
Меньший катет оказался равным 10, тогда больший катет, который вдвое больше, будет равен 20.
Задание. Найдите площадь фигуры, показанной на рисунке. Сторона каждой клеточки имеет длину, равную единице:
Решение. Эту фигуру можно разбить на квадрат со стороной 8 и два прямоугольных треуг-ка, то есть всего на три фигуры:
Подсчитаем площадь каждой из трех фигур по отдельности:
Чтобы найти площадь всей фигуры, достаточно просто сложить три полученных числа:
Задание. Вычислите площадь треуг-ка, изображенного на рисунке (площадь каждой отдельной клеточки составляет единицу):
Решение. Здесь проблема заключается в том, что треуг-к прямоугольным не является. Однако можно построить прямоуг-к, который будет состоять сразу из 4 треуг-ков:
Мы можем найти как площадь всего прямоугольника (обозначим ее как S), так и площади трех прямоугольных треуг-ков S1, S2 и S3:
Площадь произвольного треугольника
Перейдем к более сложному случаю, когда необходимо подсчитать площадь произвольного треугольника, не являющегося прямоугольным. Предположим, надо найти площадь произвольного ∆АВС. Опустим из А на сторону ВС высоту АН:
В результате мы получили два прямоугольных треуг-ка, ∆АВН и ∆АCН. Мы уже знаем, как найти их площади:
Общая площадь всего ∆АВС равна сумме площадей ∆АВН и ∆АСН. Запишем ее и вынесем общий множитель АН/2 за скобки:
В скобках стоит сумма ВН + НС. Но ведь эта сумма равна длине стороны ВС! Тогда окончательно формулу можно записать в виде:
Получили, что для вычисления площади произвольного треугольника надо сначала умножить его высоту на сторону, на которую она падает, а далее поделить результат на 2. Однако для полного доказательства этого факта надо рассмотреть особый случай, когда высота в треуг-ке падает не на сторону, а на ее продолжение (такая ситуация возникает в тупоугольном треуг-ке):
На рисунке снова получились всё те же прямоугольные треуг-ки ∆АСН и ∆АВН. Запишем формулы их площади:
Отличие в том, что на этот раз площадь АВС можно вычислить не как сумму, а как разницу этих площадей:
Итак, можно сформулировать следующее правило:
Примечание. Часто сторону, на которую опущена высота, называют основанием треуг-ка.
Задание. Вычислите площадь ∆АВС, если сторона АВ имеет длину 7, а высота СН равна 4.
Решение. В данной задаче на сторону длиной 7 падает высота длиной 4. Надо просто подставить эти числа в формулу:
Задание. Докажите, что медиана треуг-ка разбивает его на два равновеликих треуг-ка.
Пусть в ∆АВС проведена медиана СМ. Требуется доказать, что
Важно заметить, что СН будет являться высотой не только для ∆АВС, но также и для ∆СВМ и ∆САМ. Обозначим СН как h, а АВ как а. Тогда мы можем найти длины отрезков ВМ и АМ, ведь медиана делит сторону АВ пополам:
Получили одно и то же значение, то есть площади треуг-ков равны.
В рассмотренной задаче мы использовали тот факт, что у нескольких треуг-ков может быть общая высота. Общая высота используется и в многих других геометрических задачах.
Задание. Предложите способ, как разделить треуг-к, показанный на рисунке, на три равновеликих треуг-ка:
Чтобы треуг-ки были равновелики, достаточно, чтобы у них была общая высота, а основания, на которые эта высота падает, были бы равны друг другу. Поэтому можно просто поделить нижнюю сторону на три одинаковых отрезка (длиной по 7 клеток) и соединить концы полученных отрезков с противоположной вершиной:
Красной линией здесь показаны границы треуг-ков, а штриховой – их общая высота СН. Вычислить площадь каждого из треуг-ков можно по следующим формулам:
Но отрезки BD, DE и EA одинаковы (по 7 клеточек), поэтому одинаковы будут и площади:
Заметим, что необязательно делить на три одинаковых отрезка именно нижнюю сторону. Допустимы и два других варианта решения:
Но и это не единственные решения задачи. Попробуйте самостоятельно предложить ещё несколько вариантов.
Формула площади треуг-ка показывает, что между длинами высот и сторон есть взаимосвязь.
Задание.В ∆РЕТ РЕ = 72, ЕТ = 45. Высота ТН имеет длину 40. Найдите высоту РМ.
Зная ТН и РЕ, мы сможем найти площадь треуг-ка:
Теперь запишем эту формулу площади в ином виде, когда используется высота МР и сторона ЕТ
Величину SРЕТ мы только что вычислили, а длина ЕТ известна из условия, поэтому можно подставить их в формулу:
Площадь параллелограмма
Для вычисления площади параллелограмма введем понятие «высота параллелограмма». Так называют перпендикуляр, опущенный на сторону параллелограмма (ее в такой ситуации часто называют основанием) из одной из вершин параллелограмма. Важно понимать, что высоты могут упасть не на само основание, а на его продолжение. Так как у каждого параллелограмма есть 4 вершины, а из каждой из них можно опустить высоту на две противоположных вершины, то всего у параллелограмма должно быть 8 высот:
На рисунке синим показаны высоты параллелограмма, а красным цветом отмечены продолжения оснований. Оказывается, что площадь параллелограмма равна произведению его высоты и основания, на которую она опущена. Докажем это.
Опустим в параллелограмме АВСD высоты ВН и СК:
В результате получили четырехуг-к ВНКС, который является прямоугольником, ведь все его углы прямые. Очевидно, что ∆АВН и ∆DCK равные. Это можно доказать тем, что они являются прямоугольными, у них есть одинаковые гипотенузы АВ и CD (они равны как противоположные стороны параллелограмма) и одинаковые катеты ВН и СК (это уже противоположные стороны прямоугольника ВНКС).
Раз они равны, то одинаковы и их площади:
Но величину S3 можно заменить на S2. В свою очередь полученная сумма равна площади прямоугольника ВНКС, которая может быть вычислена как произведение его смежных сторон:
Но ВН – это высота, а НК – основание параллелограмма. То есть мы доказали следующее утверждение:
Задание. Найдите площадь параллелограмма, изображенного на рисунке:
Решение. По рисунке несложно определить длину как основания, так и высоты параллелограмма:
Далее надо просто перемножить эти длины:
Примечание. Конечно, если вы вдруг забыли формулу площади параллелограмма, можно просто разделить его на прямоугольник и два прямоугольных треуг-ка:
Дальше можно просто посчитать по отдельности S1, S2и S3, после чего сложить их. Попробуйте сделать это самостоятельно.
Решение. В данной задаче не потребуется даже рисунок. Обозначим высоту буквой h, тогда основание, которое вдвое длиннее, составляет 2h. Произведение этих чисел – это площадь, то есть оно равно 162:
Высота равна 9, а основание будет вдвое больше, то есть его длина равна 18.
Задание. Смежные стороны параллелограмма ABCD имеют длину 12 и 14 см, а угол между ними равен 30°. Вычислите его площадь.
Решение. Опустим на сторону длиной 14 см высоту:
Для вычисления площади надо сначала найти высоту ВН. Её можно определить из ∆АВН. Он является прямоугольным, а его острый угол∠А = 30°. У такого треуг-ка катет, лежащий против 30°, вдвое меньше АВ:
Площадь ромба
Многие четырехуг-ки, изученные нами ранее, являются частными случаями параллелограмма. Для прямоугольника и квадрата мы уже знаем формулы вычисления площади. Осталось разобраться с ромбом. Ясно, что его площадь можно найти также, как и у параллелограмма. Однако площадь ромба можно посчитать и зная только его диагонали.
Построим ромб и проведем в нем диагонали:
Нам уже известно, что диагонали ромба пересекаются под прямым углом, а точка их пересечения является серединой для каждой диагонали:
Получается, что диагонали разбивают ромб на 4 одинаковых прямоугольных треуг-ка. Высчитаем, к примеру, SAOB:
В результате мы доказали следующее утверждение:
Задание. Одна диагональ ромба равна 3,2 дм, а другая составляет 14 см. Найдите его площадь.
Решение. Для начала надо перевести все длины в одинаковые единицы измерения. Заменим дециметры на сантиметры:
Задание. Одна диагональ ромба в три раза длиннее другой, а площадь фигуры составляет 150. Вычислите длину диагоналей ромба.
Решение. Обозначим меньшую диагональ как х, тогда вторая будет равна 3х. Выразим площадь через х:
Вторая диагональ ромба будет втрое длиннее, то есть ее длина равна 3•10 = 30
Ответ: 10 и 30 см.
Площадь трапеции
Осталось рассмотреть единственный известный нам вид четырехуг-ка, который не является параллелограммом. Это трапеция. Для вычисления ее площади также потребуется высота. Под ней подразумевают перпендикуляр, опущенный из вершины трапеции на одно из ее оснований. Другими словами, высота трапеции – это расстояние между основаниями трапеции.
В произвольной трапеции ABCD, где АD – большее основание, опустим из В высоту (то есть перпендикуляр) на AD, а из D– высоту на ВС. Также проведем диагональ ВD:
Ясно, что общая площадь трапеции будет равна сумме площадей ∆АВDи ∆ВСD. В свою очередь площадь каждого из них можно подсчитать по стороне и опущенной на нее высоте. Высоты мы как раз и провели, это ВН и DK, поэтому можно записать:
Теперь заметим, что отрезки ВН и КD одинаковы, ведь фигура ВНDК является прямоугольником. Тогда площадь ∆ВСD можно записать в таком виде:
В итоге мы доказали, что для вычисления площади трапеции следует ее высоту умножить на сумму длин оснований, после чего поделить результат на два. Обычно этот факт записывают следующим образом:
Задание. У трапеции АВСD основаниями являются АВ (21 см) и CD (17 см). Высота ВН составляет 7 см. Найдите площадь трапеции.
Решение. Это простая задача на использование формулы площади трапеции:
Задание. Найдите площадь прямоугольной трапеции, показанной на рисунке (площадь клеточки равна единице):
Решение. На рисунке показана прямоугольная трапеция. Её высота равна длине ее правой боковой стороны трапеции. Покажем размеры, необходимые нам для выполнения расчета:
Задание. Тупой угол равнобедренной трапеции составляет 135°. Проведенная из этого угла высота делит противолежащее основание на отрезки длиной 14 и 34 см. Какова площадь трапеции?
Решение. Выполним построение:
Найдем острый угол трапеции. Так как CD||АВ, то
Рассмотрим ∆АDH. Он прямоугольный, а один из его острых углов равен 45°. Тогда и второй острый угол также равен 45°. То есть это равнобедренный треуг-к. Это помогает найти длину высоты DH:
ведь это прямоугольныетреуг-ки с равными гипотенузой и катетом:
Из равенства треуг-ков следует, что
Итак, сегодня мы узнали, как вычислять площади треуг-ков и некоторых видов четырехуг-ков. В большинстве случаев предварительно необходимо найти высоту в многоугольнике. В будущем мы узнаем ещё несколько формул для вычисления площадей фигур.
Прямоугольный треугольник формулы
Прямоугольный треугольник – это треугольник, у которого один из углов прямой (90°).
Другие виды треугольников:
Любой прямоугольный треугольник характеризуется катетами a и b и гипотенузой c (см. рисунок).
Катет – это сторона прямоугольного треугольника, образующая прямой угол с другой стороной (также катетом).
Гипотенуза – это сторона прямоугольного треугольника, лежащая напротив прямого угла.
Именно эти характеристики используются в формулах прямоугольного треугольника при вычислении площади, периметра, а также радиусов вписанной и описанной окружностей.
Формула радиуса вписанной окружности для прямоугольного треугольника
Радиус вписанной окружности r можно вычислить, зная стороны прямоугольного треугольника:
Формула радиуса описанной окружности для прямоугольного треугольника
Радиус описанной окружности R можно вычислить, зная гипотенузу прямоугольного треугольника:
Формула периметра прямоугольного треугольника
Периметр P прямоугольного треугольника можно получить, зная его стороны:
При вычислении площади прямоугольного треугольника часто требуется знать его полупериметр:
p = P/2 = (a + b + c)/2
Формулы площади прямоугольного треугольника
При вычислении площади прямоугольного треугольника можно пользоваться формулами, которые применяются для вычисления площади произвольного треугольника, так как прямоугольный треугольник является частным случаем для треугольников.
Площадь прямоугольного треугольника S можно вычислить, зная его катеты a и b:
Еще одна формула позволяет вычислить площадь прямоугольного треугольника по его катетам a и b и полупериметру p (формула Герона):
Поделитесь статьей с одноклассниками «ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК формулы площади, периметра, радиуса».