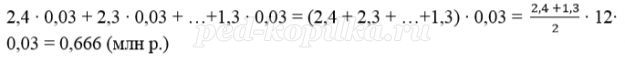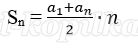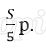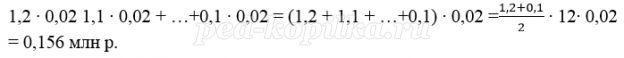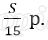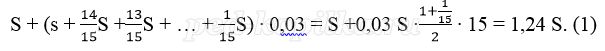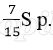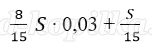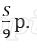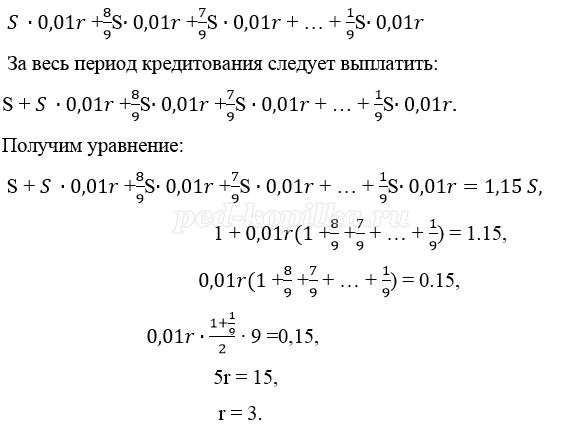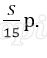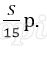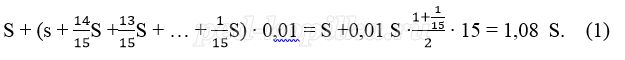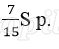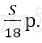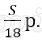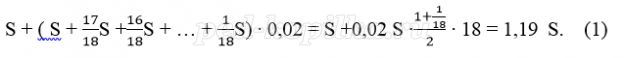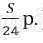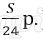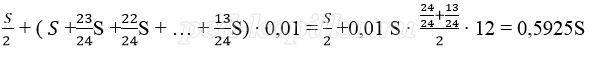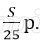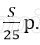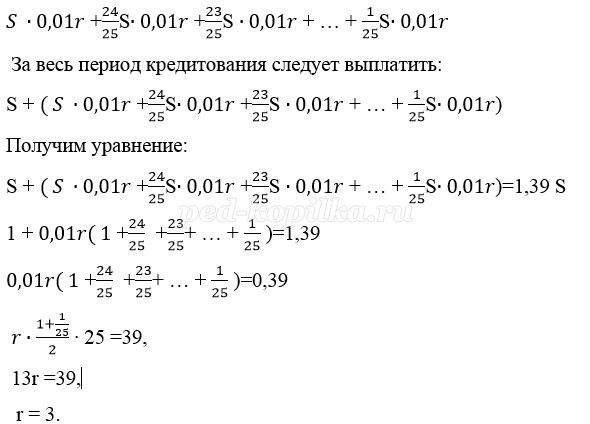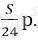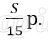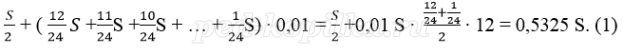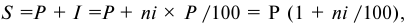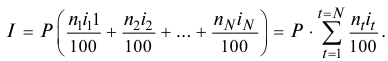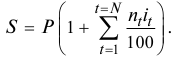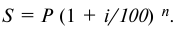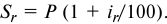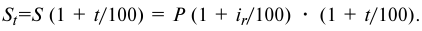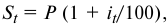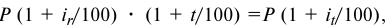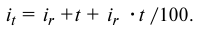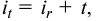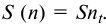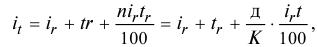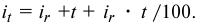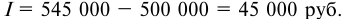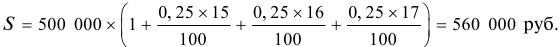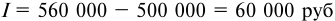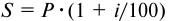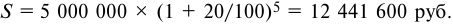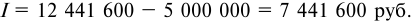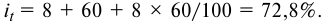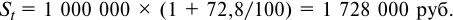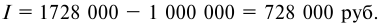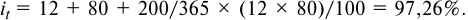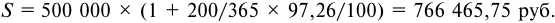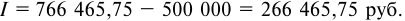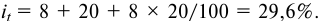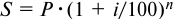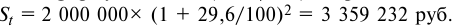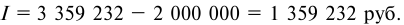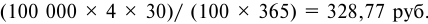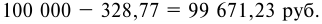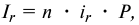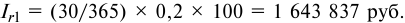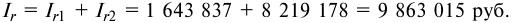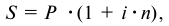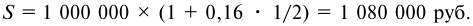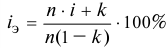задача про кредит с решением
Решение экономических задач на кредиты
Задача 2.
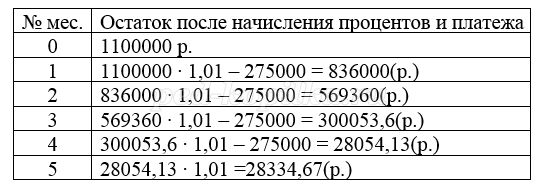
31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5 годовых. Схема выплаты кредита следующая – 31 декабря следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк х рублей. Какой должна быть сумма х, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)?
Решение:
Дмитрий взял в банке кредит 4 290 000 рублей.
При решении задач на кредиты с дифференцированным платежом начисляемые проценты за весь период кредитования можно вычислить с помощью формулы суммы n-первых членов арифметической прогрессии. И потом найти сумму общего платежа. Считаю, что этот метод будет прост и понятен для учащихся.
Задача 3
15 января планируется взять кредит в банке на сумму 2,4 млн. рублей на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Какую сумму надо выплатить банку за первые 12 месяцев?
Решение:
Платёж за месяц состоит из величины ежемесячного долга (он равен 2400000:24=100000(р.)) и начисленных к остатку процентов. В каждый месяц долг уменьшается 100000р.
Сумма начисленных «процентов» за 12 месяцев (в млн. р.):
За 12 месяцев буде выплачена половина долга, то есть 1,2 млн р.
Значит за первые 12 месяцев банку нужно выплатить 1 200 000 + 666 000 = 1 866 000 р.
Ответ: 1 866 000 рублей.
Задача 4
15 января планируется взять кредит в банке на 5 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?
Решение:
Пусть в банке взяли кредит S рублей. Платёж за месяц состоит из величины ежемесячного долга (он равен
Всего банку будет выплачено S + 0,03S = 1,03S. Значит общая сумма выплаченных денег от суммы кредита составляет 103%.
Ответ: 103%.
Задача 5
15 января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно выплатить банку за последние 12 месяцев?
Решение:
Платёж за месяц состоит из величины ежемесячного долга (он равен 2400000:24=100000(р.)) и начисленных к остатку процентов. В каждый месяц долг уменьшается 100000р.
Сумма начисленных процентов за 12 последних месяцев (в млн):
За 12 месяцев буде выплачена половина долга, то есть 1,2 млн р.
Значит за последние 12 месяцев банку нужно выплатить 1 200 000 + 156 000 = 1 356 000 р.
Ответ: 1 356 000 рублей.
Задача 6
15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что восьмая выплата составила 99,2 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
Значит за весь срок кредитования будет выплачено 1 488 000 рублей.
Ответ: 1 488 000 рублей.
Задача 7
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 15% больше, чем сумма взятая в кредит. Найдите r.
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
Значит кредит взят под 3% в месяц.
Ответ: 3%.
Задача 8
15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что восьмая выплата составила 108 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
В (1) подставим (2), получим: 1,08 ∙1 500 000 = 1620000
Значит за весь срок кредитования будет выплачено 1 620 000 рублей.
Ответ: 1 620 000 рублей.
Задача 9
15 января планируется взять кредит в банке на 18 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь период кредитования?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
Значит сумма выплаченных банку денег составляет 119% от суммы долга.
Ответ: 119%.
Задача 10
15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что за первые 12 месяцев нужно выплатить банку 177,75 тыс. рублей. Какую сумму планируется взять в кредит?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
Получим уравнение: 0,5925 S = 177750,
S = 300000
Значит в кредит взяли 300 000 рублей.
Ответ: 300 000 рублей.
Задача 11
15 января планируется взять кредит в банке на 25 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что я сумма денег, которую нужно выплатить банку за весь срок кредитования, на 39% больше, чем сумма, взятая в кредит. Найдите r.
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
Значит кредит взят под 3% в месяц.
Ответ: 3%.
Задача 12
15 января планируется взять кредит в банке на 24 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что за последние 12 месяцев нужно выплатить банку 1597,5 тысяч рублей. Какую сумму планируется взять в кредит?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
Получим уравнение: 0,5325 S = 1597500; S = 3 00 000.
Значит планируется взять 3 000 000 рублей.
Ответ: 3 000 000 рублей.
Литература
И.В.Ященко. Математика. Профильный уровень. Типовые тестовые задания. Издательство «Экзамен», М. 2017.
Кредитные операции с примерами решения задач
Кредитные операции
Кредитные операции играют основную роль в деятельности банков. Ставка, по которой выдаются кредиты, превышает ставку, по которой принимаются депозиты, на величину процентной маржи, которая и является источником прибыли банка от кредитных операций. При погашении кредита удобно сразу определять размер возвращаемой (погашаемой) суммы, равной сумме кредита 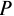
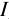
где 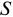
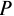
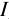
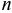
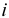
Если ставка процентов в течение срока кредита по условиям кредитного договора будет изменяться, размер погашаемой суммы можно определить, применяя формулу 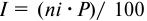
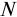
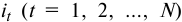
Сумма кредита с процентами определяется по формуле
При выдаче кредитов на срок больше года проценты могут начисляться по сложной годовой ставке. Погашаемая сумма кредита может быть при этом определена с использованием формулы
При начислении процентов за кредит следует учитывать инфляцию. Ставку процентов при выдаче кредитов в условиях инфляции можно определить следующим образом. Если задана реальная доходность кредитной операции, определяемая простой ставкой процентов 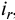
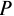
Эквивалент такой суммы в условиях инфляции составит:
С другой стороны, величину 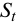
где 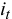
Приравняв два последних выражения, получаем
откуда простая ставка процентов, обеспечивающая реальную эффективность кредитной операции 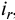
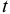
При проведении подобных расчетов часто пользуются приближенным выражением
из которого следует, что
Следовательно, если кредит был выдан по ставке 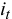
Если срок, на который выдается кредит, меньше срока, за который определяется расчетный уровень инфляции, необходимо задать зависимость значения 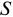
При заданном годовом уровне инфляции 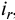
где 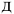
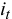
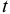
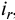
Задача 71.
Банк выдал кредит в размере 500 тыс. руб. на шесть месяцев по простой ставке процентов 18% годовых. Требуется определить:
1) погашаемую сумму.
2) сумму процентов за кредит.
Решение:
Задача 72.
Банк выдал кредит в сумме 500 тыс. руб. на три квартала по простой ставке процентов, которая в первом квартале составила 15% годовых, а в каждом последующем увеличивалась на 1 процентный пункт. Требуется определить:
1) погашаемую сумму;
2) сумму процентов за пользование кредитом.
Решение:
1. По формуле (5.2) определяем погашаемую сумму:
Задача 73.
Банк выдал долгосрочный кредит в размере 5 млн. руб. на пять лет по годовой ставке сложных процентов 20% годовых. Кредит должен быть погашен единовременным платежом с процентами в конце срока. Требуется определить:
1) погашаемую сумму
2) сумму полученных процентов.
Решение:
определяем погашаемую сумму:
Задача 74.
Банк выдал кредит в 1 млн руб. на год. Требуемая реальная доходность операции равна 8% годовых, ожидаемый годовой уровень инфляции принят равным 60%. Требуется определить:
1) ставку процентов по кредиту.
2) погашаемую сумму и сумму полученных процентов.
Решение:
Сумму полученных процентов определяем так:
Задача 75.
Кредит в 500 тыс. руб. выдан на 200 дней. Расчетный уровень инфляции за год принят равным 80%, реальная доходность операции должна составить 12% годовых, количество дней в году равно 365. Требуется определить:
1) ставку процентов при выдаче кредита
2) погашаемую сумму и сумму полученных процентов.
Решение:
Сумма полученных процентов составит:
Задача 76.
Кредит в 2 млн руб. выдан на два года. Реальная эффективность операции должна составить 8% годовых по сложной ставке процентов. Расчетный уровень инфляции 20% в год. Требуется определить:
1) ставку процентов при выдаче кредита;
2) погашаемую сумму и сумму полученных процентов. Решение
определим погашаемую сумму:
Сумма полученных процентов будет равна:
Задача 77.
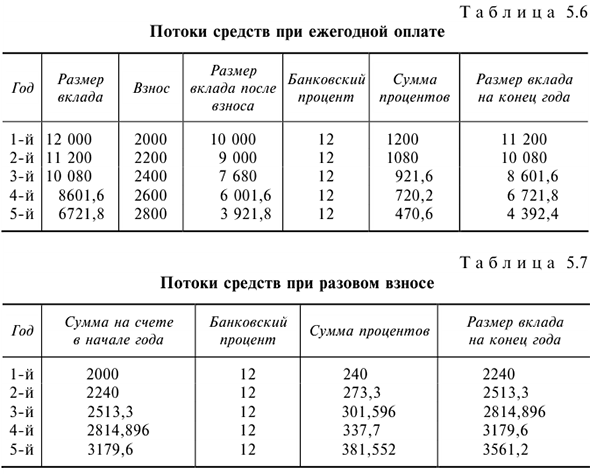
Базовая годовая сумма оплаты обучения в вузе равна 2000 руб. и повышается с учетом инфляции (10%). Срок обучения пять лет. Вуз предлагает выплатить сразу 10 тыс. руб., оплатив весь срок обучения. Банковский процент на вклад составляет 12%, сумма вклада равна 12 тыс. руб. Требуется определить, выгодно ли это предложение для студента.
Решение:
Проведем расчеты в табл. 5.6 и 5.7.
По результатам расчетов видно, что первый вариант выгоднее.
Задача 78.
В расчет за поставку фирма 
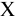
2) сумму, которую банк выплачивает фирме 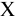
Решение:
Используем формулу расчета дисконта:
Задача 79.
Заемщик берет ссуду на сумму 100 тыс. руб. сроком на шесть месяцев. Через шесть месяцев заемщик возмещает 102 тыс. руб., т.е. ссуду — 100 тыс. руб. и проценты — 2 тыс. руб. Требуется определить годовую ставку по ссуде.
Решение:
Задача 80.
Банк выдал в начале квартала кредит на сумму 100 млн руб. сроком на один месяц по ставке 20% годовых и через месяц кредит на сумму 200 млн руб. сроком на два месяца по ставке 25% годовых. Требуется определить сумму процентов за кредиты (полученный доход).
Решение:
где 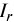
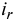
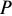
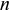
Задача 81.
Банк выдал ссуду в размере 1 млн руб. на шесть месяцев по простой ставке процентов 16% годовых. Требуется определить: сумму погашения.
Решение:
где 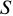
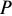
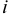
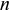
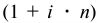
Задача 82.
При выдаче кредита на шесть месяцев по ставке 16% годовых удержаны комиссионные в размере 2% суммы кредита. Требуется определить доход банка с учетом удержания комиссионных.
Решение:
Используем следующую формулу:
где 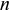
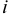
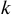
Доход банка составит в данном случае:
Эта лекция с примерами решения взята со страницы решение задач по предмету «деньги кредит банки»:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института