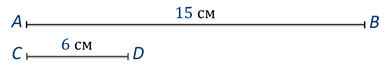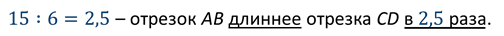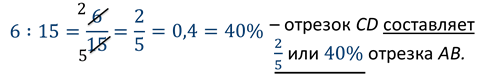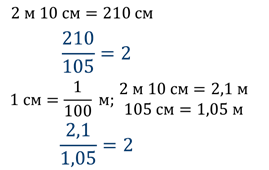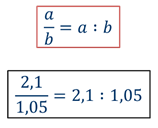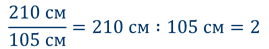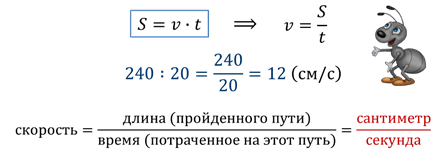задачи на отношения 6 класс с решением и ответами
Отношения
Урок 20. Математика 6 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Отношения»
Для решения практических задач человеку часто приходится сравнивать разные значения одной и той же величины – массы, расстояния, времени, скорости, стоимости, объёма, площади и т.д.
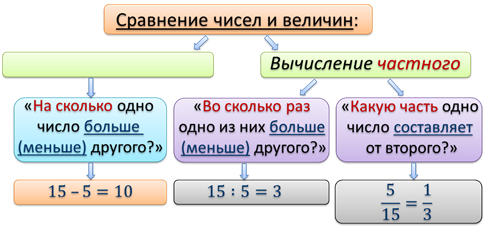
Для сравнения чисел и величин существуют, как вы знаете, два способа:
1-ый: вычисление разности и 2-ой: вычисление частного.
Оба этих способа используют часто при решении практических задач, но служат они для разных целей. К делению прибегают в тех случаях, когда хотят получить качественную оценку или относительную оценку той или иной ситуации.
На экране изображены два отрезка. Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Во сколько раз отрезок АВ больше или длиннее отрезка CD?
Вторая задача: на экране изображены эти же два отрезка. Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Но поставим вопрос по-другому: какую часть отрезок CD составляет от отрезка АВ?
Обе рассмотренные задачи решаются делением, и ответ даётся в виде частного. В таких случаях частное двух чисел называют их отношением.
Частное двух не равных нулю чисел (или двух величин) называют отношением.
Сами эти числа (величины) называют членами отношения.
Иными словами, отношение двух чисел – это другое название их частного. Отношение чисел записывают с помощью знака деления, а также с помощью черты обыкновенной дроби.
Частные чисел читают так:
Напомним, что отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого.
Черта дроби используется для записи отношения и тогда, когда его члены не являются натуральными числами.
Рост дяди Степы 2 м 10 см, а рост мальчика Васи – 105 см. Во сколько раз дядя степа выше мальчика Васи?
Но ведь дробную черту мы использовали для записи дробей! А сейчас записана не дробь. Верно. Но вы давно знаете, что при записи деления натуральных чисел вместо знака деления можно использовать дробную черту. Так вот, договариваются о том же и при записи деления любых чисел.
Итак, если а и b – любые числа, то
Сделаем важное замечание:
Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.
Отношение величин одного наименования (длин, скоростей, стоимостей и т.д., выраженных одинаковыми единицами измерения) есть число. Такие величины называют однородными.
Отношение величин разных наименований (пути и времени, стоимости товара и его количества, массы тела и его объема и т.д.) есть новая величина.
Вот, например, в предыдущей задаче мы находили во сколько раз дядя Степа выше мальчика Васи.
Рост Васи и рост дяди Степы – это однородные величины, т.е. длина. Поэтому отношение их роста выраженно натуральным числом.
А теперь давайте разберёмся, почему отношение разноимённых величин – это новая величина.
Муравей за 20 секунд пробегает 240 сантиметров. Определите скорость движения муравья.
Отметим, что обозначения км/ч, м/с и т.п. приняты именно потому, что расстояние делят на время. Их обычно записывают с наклонной чертой.
В виде отношений определяются и другие величины:
Из основного свойства частного следует свойство отношения.
Давайте вспомним основное свойство частного:
если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Следовательно, получаем свойство отношения:
отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Мы с вами убедились, что свойство отношения действует. Мы умножили числитель и знаменатель дроби на одно и то же число, само же отношение не изменилось.
Итак, сегодня на уроке мы узнали, что частное двух не равных нулю чисел (или двух величин) называют отношением.
Сами эти числа (величины) называют членами отношения.
Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.
И свойство отношения: отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Урок 21 Бесплатно Отношения
В этом уроке мы узнаем, что такое отношения. Также поймем, что нам показывает отношение двух чисел. И в завершение узнаем, как определить часть одного числа от другого.
Отношение
Начнем с определения:
Отношением двух чисел называют частное этих двух чисел.
Записать отношение числа a к числу b мы можем как \(\mathbf\) или же через дробную черту: \(\mathbf<\frac>\)
У нас получается дробное выражение, поэтому возможны варианты во что оно преобразуется:
Посмотрим на разные примеры.
Пример 1
Найдем отношение чисел 256 и 8
По определению, отношением двух чисел будет являться их частное, что мы и посчитаем.
Ответом будет 32.
Иными словами, 256 относится к 8 как 32 к 1
В последней фразе была как раз упомянута суть отношения, мы акцентируем на этом внимание.
Отношение одного числа к другому показывает, как одно число соотносится с другим, иными словами, во сколько раз оно его больше или меньше:
Пример 2
Найдите отношение 15 к 12
По определению посчитаем частное, а далее посмотрим на полученный результат.
Данный пример иллюстрирует, в каких случая получается смешанное число.
Отношение равняется смешанному числу в тех случаях, когда первое число больше второго, и при этом первое на второе не делится.
Мы можем прочитать результат так: 15 больше 12 в \(\mathbf<1\frac<1><4>>\) раза.
Пример 3
Найдем отношение 16 к 24.
Снова идем по алгоритму: делим первое число на второе.
В этом случае мы получили в ответе правильную дробь.
Нам это говорит о том, что первое число меньше второго.
А если мы хотим сказать, как именно первое число меньше второго, то это можно сделать так: первое число меньше второго в \(\mathbf<\frac<2><3>>\) раза.
Мы можем сформулировать вывод и так: 16 составляет \(\mathbf<\frac<2><3>>\) от 24-х, то есть мы отвечаем на вопрос, какой частью является первое число от второго.
Также важно отметить, что отношение числа a к числу b не всегда равно отношению числа b к числу a.
Пример 4
Есть два числа, 14 и 28
Посчитаем отношение 14 к 28
И посчитаем отношение 28 к 14
Как вы видите, получились разные значения.
Как можно заметить, это взаимно обратные числа.
Отметим еще одно свойство отношений: если есть два числа a и b, то отношение a к b взаимно обратно отношению b к a.
Если дано отношение первого числа ко второму, то мы без труда сможем найти отношение второго к первому, даже не зная самих чисел, просто посчитав обратное к отношению число.
Пример 5
Дано, что отношение числа a к числу b равно \(\mathbf<\frac<2><5>>\), найдем отношение b к a
Для этого надо найти обратное число к \(\mathbf<\frac<2><5>>\)
Значит, отношение b к a равняется \(\mathbf<2\frac<1><2>>\)
В конце этой части добавим еще одно простое, но важное свойство.
Отношение двух чисел не изменится, если каждое из них домножить или разделить на одно и тоже число.
Это легко доказать, показав, что при делении этот множитель сократится.
Пример 6
Отношение числа 10 к числу 30 равно \(\mathbf<\frac<1><3>>\)
Домножим каждое из чисел на 2 и заметим, что отношение 20 к 60 также равно \(\mathbf<\frac<1><3>>\)
Пройти тест и получить оценку можно после входа или регистрации
Отношение и часть от числа
Посмотрим, какие еще можно сделать выводы, зная отношение.
Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь.
Так мы получим число, которое будет частью исходного.
Допустим, изначально у нас было число 4, и мы решили найти от него \(\mathbf<\frac<3><8>>\)
Перемножив, мы получим:
А теперь найдите отношение полученного числа к изначальному.
Для этого разделите одно на другое:
То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение.
Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби.
Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b.
Пример 1
Известно, что некая дробь от числа 10 равна \(\mathbf<2\frac<1><2>>\)
Найдем, какая именно это дробь.
Решение:
Дробь от числа равна отношению полученного числа к изначальному.
Теперь разделим одно на другое и получим ответ.
Ответ: дробь, взяв которую от 10 получили \(\mathbf<2\frac<1><2>>\), равняется \(\mathbf<\frac<1><4>>\)
Пример 2
Отношение первого числа ко второму равно \(\mathbf<1\frac<1><5>>\), также известно, что первое число равно 6.
Найдем второе число.
Решение:
Мы знаем, что отношение обратно дроби.
Найдем обратное число к \(\mathbf<1\frac<1><5>>\)
Теперь можно найти второе число, домножим первое на эту дробь:
Второе число равно 5
Проверка:
Найдем отношение первого числа ко второму, то есть 6 к 5
Получилось то же отношение, что и в условии.
Пример 3
Решим похожую задачу:
Отношение числа а к числу b равно \(\mathbf<1\frac<1><2>>\)
Известно, что число b равняется 8-ми, надо найти число а.
Решение:
Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения:
Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь.
В нашем случае на дробь надо делить число b :
Ответ: число a равняется 12
Пройти тест и получить оценку можно после входа или регистрации
Отношения в задачах
Теперь научимся находить отношения в задачах.
Сразу перейдем к примерам, чтобы посмотреть, за какими формулировками могут стоять отношения.
Задача 1
Длина улицы составляет 25 километров. Освещено 15 километров улицы.
а) Найдите, какая часть улицы освещена.
б) Во сколько раз вся улица длиннее ее освещенной части?
Решение:
В начале урока мы находили отношение меньшего числа к большему, тем самым определили, какую часть первое число составляет от второго.
Именно это и спрашивается в первом вопросе.
Для нахождения отношения длины освещенного участка к длине всей улицы поделим одну величину на другую:
Значит, длина освещенного участка составляет \(\mathbf<\frac<3><5>>\) от длины всей улицы.
Для нахождения этого отношения необходимо поделить длину всей улицы на длину ее освещенной части:
Что отвечает на вопрос второго пункта.
Также важно помнить, что если подаются какие-либо величины, то всегда надо следить, чтобы мера измерения была одинаковой.
То есть если нам подали что-то в тоннах и килограммах и мы хотим найти отношения этих величин, то надо либо тонны переводить в килограммы, либо наоборот.
Задача 2
Масса груза составляет 2 тонны. Известно, что часть груза- это одежда и ее масса 350 кг.
Найдите, какую часть от массы груза составляет масса одежды.
Решение:
Для начала преобразуем преобразуем тонны в килограммы. Получается, что масса груза равна 2000 кг.
Теперь найдем искомое отношение:
Теперь попробуйте порешать задачи самостоятельно, а если будет сложно, используйте подсказки.
Пройти тест и получить оценку можно после входа или регистрации
Интересная информация
Сегодня вы узнаете о математических фокусах!
Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам.
Фокус 1
Попросите зрителя загадать число и никому не говорить.
Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число.
Теперь вы можете уверенно сказать, что у зрителя получилось число 4.
Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка.
Попробуй доказать это на формулах, взяв за задуманное число Х
Фокус 2
В нем вы можете угадать День рождения человека.
Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.).
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Задачи на тему отношения
1 От куска материи длиной 5 м отрезали 2 м. Какую часть куска материи отрезали?
РЕШЕНИЕ
3 Масса станка 9,6 ц, а электромотора 36 кг. Найдите отношение массы электромотора к массе станка.
РЕШЕНИЕ
722 Найдите отношение 124 к 3; 6 к 20; 12,3 к 3; 9,1 к 0,07; 0.25 к 0,55
РЕШЕНИЕ
723 Проволока разрезана на два куска. Первый кусок имеет длину 9 м, а второй 14,4 м. Найдите, какую часть всей проволоки составляет первый и второй кусок. Какую часть первый кусок составляет от длины второго
РЕШЕНИЕ
724 Внутри угла AOC проведен луч OB так, что AOB = = 56° и BOC = 40°. Какую часть угла AOC составляет AOB; BOC? Выполните построение этих углов с помощью транспортира.
РЕШЕНИЕ
725 Площадь прямоугольника 22,05 дм2. Длина 10,5 дм. Найдите отношение длины прямоугольника к его ширине. Что показывает это отношение? Запишите отношение, обратное полученному отношению. Что оно будет показывать
РЕШЕНИЕ
726 Отношение a к b равно 2/7. Найдите обратное отношение. Чему будет равно отношение m к n, если n к m 1,25?
РЕШЕНИЕ
727 Сплав из свинца и олова содержит 1,52 кг свинца и 0,76 кг олова. В каком отношении взяты свинец и олово? Какую часть сплава по массе они составляют
РЕШЕНИЕ
728 Какую часть урока заняла самостоятельная работа, которая длилась 20 мин, если продолжительность урока 45 мин?
РЕШЕНИЕ
729 В классе 36 учащихся. Из них 15 мальчиков, а остальные девочки. Какую часть учащихся составляют мальчики и девочки? Чему равно отношение их числа и что оно показывает?
РЕШЕНИЕ
730 Между двумя городами построили дорогу. Первый город построил 5/7 дороги,второй остальную часть. Во сколько раз часть дороги,построенная первым городом, больше, чем вторым?
РЕШЕНИЕ
732 Молоко разлили в три бидона. В первый налили 0,1 всего молока, во второй 0,3, а в третий 0,6. Что показывает отношение 0,1 к 0,3; 0,1 к 0,6; 0,3 к 0,6; (0,3+ 0,1) к 0,6?
РЕШЕНИЕ
733 В классе 40 учащихся. 8 учащихся учатся на 5. Сколько процентов класса составляют отличники?
РЕШЕНИЕ
734 Из 250 семян погибли 10. Найдите процент всхожести
РЕШЕНИЕ
735 После установки нового оборудования завод за смену вместо 240 холодильников стал выпускать 300. На сколько процентов увеличилось производство холодильников за смену?
РЕШЕНИЕ
736 По коэффициенту трудового участия заработок между тремя рабочими распределили следующим образом: первому 40% всех денег, второму 35%, а третьему остальные 25%. Определите, округлив результаты до десятых, сколько процентов составляли деньги, полученные первым рабочим, от денег, полученных двумя другими; вторым рабочим, от денег, полученных двумя другими; первым рабочим, от денег, полученных вторым; вторым рабочим, от денег, полученных первым; третьим рабочим, от денег, полученных первым.
РЕШЕНИЕ
737 Имеющиеся деньги брат и сестра распределили так, что сестра получила в 3 раза больше, чем брат. Определите какую часть денег получила сестра и брат; сколько процентов всех денег получила сестра и брат; какую часть деньги брата составляют от денег сестры.
РЕШЕНИЕ
738 Известно, что сумма углов любого треугольника равна 180°. В треугольнике ABC найдите A, если B = 75°, C = 80°; A больше B на 20° и меньше C на 40°; B составляет 2/3, a C 1/5 суммы всех углов треугольника; A составляет 5/6 B и C = 70°
РЕШЕНИЕ
739 Что показывает отношение пути, пройденного автомашиной, ко времени ее движения; числа деталей, изготовленных станком-автоматом, ко времени его работы; стоимости купленных яблок к их массе; объема прямоугольного параллелепипеда к площади его основания?
РЕШЕНИЕ
740 Найдите, сколько процентов число 9,729 составляет от числа 84,6. С помощью микрокалькулятора для этого можно выполнить вычисление по программе 9,729 : 84,6 % =
РЕШЕНИЕ
741 Вычислите устно.
РЕШЕНИЕ
742 Найдите пропущенные числа.
РЕШЕНИЕ
743 На сколько надо увеличить знаменатель дроби 5/12, 7/17, 8/32, 2/3, чтобы получить 1/4
РЕШЕНИЕ
744 Выразите в процентах числа: 0,2; 0,15; 1/2; 3/5; 3/4; 1/20; 1; 3
РЕШЕНИЕ
745 Половина от половины числа равна половине. Найдите это число.
РЕШЕНИЕ
746 Кто быстрее? Найдите в таблице последовательно все числа от 26 до 50
РЕШЕНИЕ
747 Найдите значение выражения.
РЕШЕНИЕ
748 На подкормку овощей и фруктовых деревьев израсходовано 2/3 из имевшихся 18 ц удобрений. На подкормку овощей пошли 3/4 израсходованных удобрений. Сколько центнеров удобрений израсходовано для овощей?
РЕШЕНИЕ
749 На окраску окон и дверей было истрачено 3,2 кг белил, что составляет 5/8 всех белил, истраченных на ремонт. На него истрачено 4/5 всех купленных белил. Сколько килограммов белил куплено?
РЕШЕНИЕ
750 Найдите объем прямоугольного параллелепипеда, если его ширина 2,5 см и составляет 5/8 высоты, а длина в 3,4 раза больше высоты; его высота 3,5 см и составляет 0,7 ширины, а длина в 2,4 раза больше ширины.
РЕШЕНИЕ
752 Крутизной лестницы называют отношение высоты ступеньки к ее глубине. Чему равна крутизна лестницы, если высота ступеньки 18 см, а глубина 30 см?
РЕШЕНИЕ
753 Автобус в первый час прошел 30 км, во второй 24 км, а в третий 42 км. Какую часть всего пути прошел автобус в каждый час? Какую часть пути, оставшуюся после первого часа движения, он прошел во второй и в третий час
РЕШЕНИЕ
754 Для варенья на 3,6 кг ягод было взято 4,2 кг сахарного песку. В каком отношении по массе были взяты ягоды и сахарный песок?
РЕШЕНИЕ
755 В сосуд налили 240 г воды и положили 10 г соли. Найдите процентное содержание соли в растворе. Через некоторое время 50 г воды испарилось. Какое теперь стало процентное содержание соли в растворе?
РЕШЕНИЕ
756 Комбайнер намолотил 76 т зерна, превысив задание на 12 т. На сколько процентов комбайнер перевыполнил задание?
РЕШЕНИЕ
757 На складе были пшеница, овес и кукуруза, причем пшеница составляла 64%, овес 16% всего количества зерна. В товарный состав загрузили всю пшеницу и кукурузу. Какой процент погруженного зерна составляла пшеница? Какой процент составляла бы пшеница, если вместо кукурузы погрузили бы овес?
РЕШЕНИЕ
758 Длина прямоугольника a см, а ширина b см. Длина другого прямоугольника m см, а ширина n см. Найдите отношение площади первого прямоугольника к площади второго. Найдите значение получившегося выражения, если a = 9, b = 2, m = 8, n = 3; a = 6,4; b = 0,2; m = 3,2; n = 0,5
РЕШЕНИЕ
759 Найдите значение выражения.
РЕШЕНИЕ
Задачи по теме «Отношения и пропорции» 6 класс
Ищем педагогов в команду «Инфоурок»
1. Задачи на отношения.
1. Отрезок АВ разделён точкой С на отрезки АС и ВС в отношении 2:7. Найти длину отрезка АВ, если длина отрезка АС на 5,5 см меньше длины отрезка ВС.
2. С двух участков собрали урожай. Каков урожай на каждом участке, если их отношение равно 11:14, а урожай, собранный со второго участка, на 18 тонн больше, чем с первого?
3. Сплав состоит из меди и цинка. Отношение массы меди к массе цинка равно 7:2. Найдите массу сплава, если масса меди на 4кг больше массы цинка в сплаве.
4. Найти массу сплава цинка и меди, если отношение массы меди к массе цинка в сплаве равно 3:5 и меди на 2,4г меньше, чем цинка.
2. Задачи на прямо пропорциональные величины.
1. Из 90 цветов, посаженных в цветнике, принялись 72. На сколько процентов меньше не принявшихся цветов, чем принявшихся?
2. 0,8 м ткани стоят 560 тенге. На сколько больше заплатят за 3,25 м ткани?
3. 4 м 3 зерна ржи весят 2,8 т. На сколько тонн больше весит 6,5 m 3 зерна ржи?
4. Поезд за 4,5 часа проехал 360 км. За какое время, двигаясь с тон же скоростью, поезд проедет расстояние, увеличенное на 80 км?
3. Задачи на обратно пропорциональные величины.
1. Все члены бригады работают в одинаковом темпе. Четверо, рабочих успевают выполнить работу за 32ч. Сколько времени понадобится для выполнения этой же работы трем рабочим?
2. Чтобы вывезти товар потребуется 21 автомашина грузоподъёмностью 2,5 т. Сколько потребовалось бы для выполнения этой работы автомашин грузоподъёмностью 3,5 т?
3. 15 рабочих закончили отделку квартир в новом доме за 24 дня. За сколько дней выполнили бы эту работу 18 рабочих?
4. Пешеход затратил на путь 2,5 ч, двигаясь со скоростью 3,6 км/ч. Сколько времени затратит пешеход на тот же путь, если его скорость будет 4,5 км/ч?
4. Задачи на масштаб.
1. Комната имеет прямоугольную форму. Размеры пола этой комнаты на плане 4см и 6см. В действительности меньшая сторона пола 5 м. Найдите площадь комнаты н масштаб плана.
2. 125 м на местности соответствуют 2,5 см на плане. Найти масштаб плана и расстояние между двумя точками на местности, если на плане оно 4,2 см.
3. План земельного участка квадратной формы выполнен в масштабе 1:500. Сторона участка на плане 16см. Вычисли площадь участка.
4. На карте расстояние между годами А и В равно 2,6см. а расстояние между городами В и С – 3,7см, На местности расстояние между- городами В и С равно 296км. Найдите расстояние на местности между годами А и В и масштаб карты.