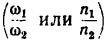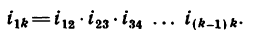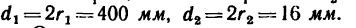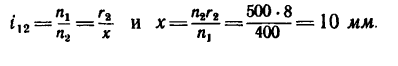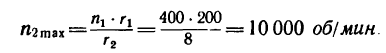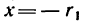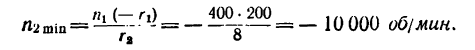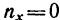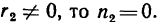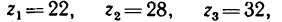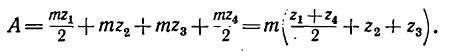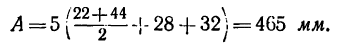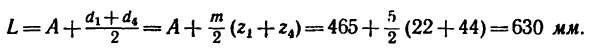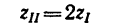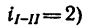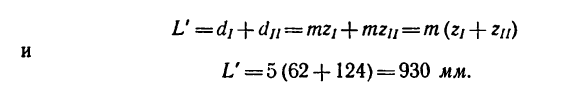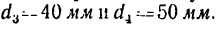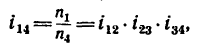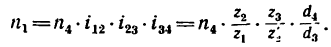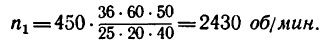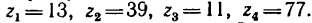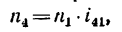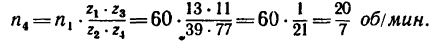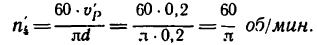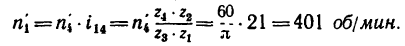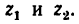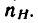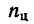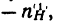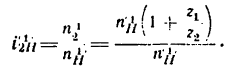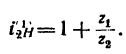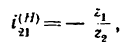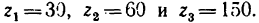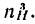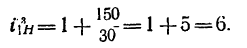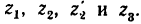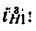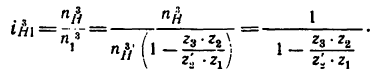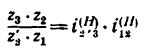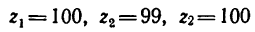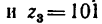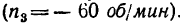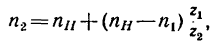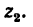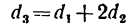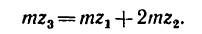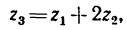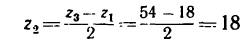задачи на передаточное отношение

Определение передаточных отношений различных передач в теоретической механике

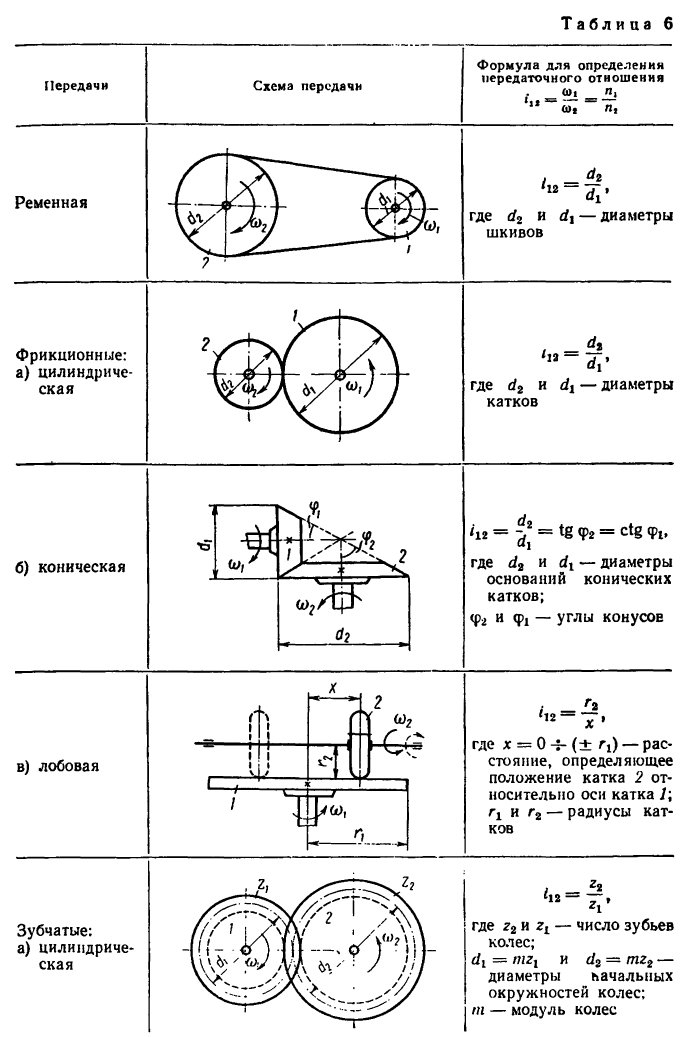
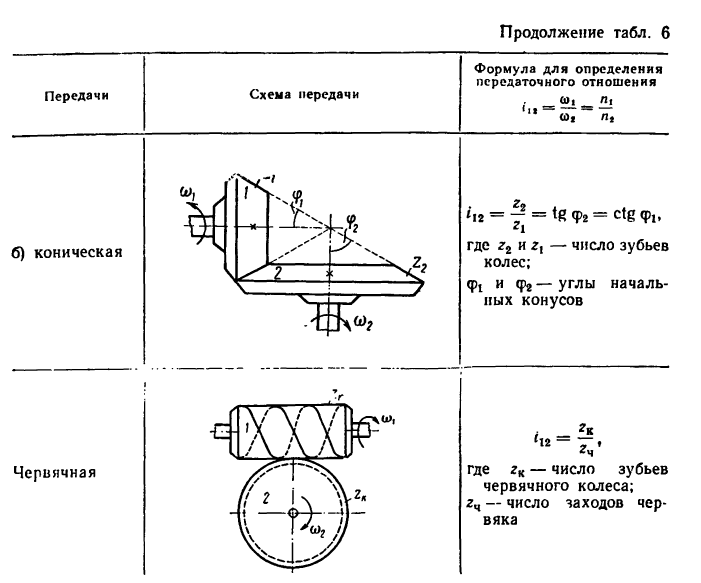
Определение передаточных отношений различных передач:

Передаточное отношение — основная кинематическая характеристика любой передачи.

Передаточные отношения определяются при помощи тех или иных геометрических элементов звеньев передачи. Найденное его значение выражает отношение угловых скоростей

Даны формулы, при помощи которых определяются передаточные отношения различных простейших передач, составленных из пары звеньев.

Передаточное отношение сложной передачи — передачи, составленной из нескольких простейших передач, равно произведению передаточных отношений простейших передач:

Передаточное отношение между двумя элементами передачи считается положительным, если оба элемента вращаются в одну сторону, например пара зубчатых колес с внутренним зацеплением.

Передаточное отношение между двумя элементами считается отрицательным, если оба элемента вращаются в противоположные стороны, например пара зубчатых цилиндрических колес с внешним зацеплением.

Задача №1

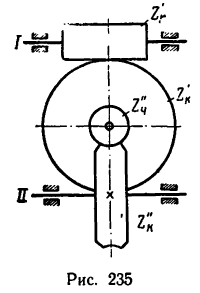
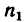
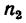
На каком расстоянии х необходимо установить каток 2 лобовой фрикционной передачи (см. эскиз к лобовой передаче в табл. 6), чтобы при угловой скорости = 400 об/мин катка 1 каток 2 вращался со скоростью = 500 об/мин? Диаметры катков

Определить также, какие наименьшую и наибольшую угловые скорости может получить вал катка 2 при различных положениях последнего.

1. Необходимое значение х (расстояние от катка 2 до оси катка I) найдем непосредственно из формулы передаточного отношения любой передачи:

2. Если начать передвигать каток 2 ближе к краю катка 1 (увеличить х), то точки на ободе катка 2 будут вступать в контакт с точками на торцовом поверхности катка 1, имеющими возрастающую скорость (по зависимостии в данном случае и благодаря силе трения станут приобретать такую же большую скорость.

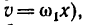
Если в выражение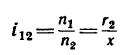
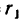
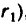
вместо х подставить наибольшее, теоретически возможное значение х — (практически xmas несколько меньше то

3. Если каток 2 установить у противоположного края катка 1, то угловая скорость у катка 2 также получится 10000 об/мин, но он будет вращаться в обратную сторону.

Таким образом, при

Благодаря способности изменять направление вращения вала, на котором укреплен каток 2, лобовую фрикционную передачу называют фрикционным вариатором (передача, способная варьировать направлением вращения).

4. При х = 0 (положение катка 2 совпадает с осью катка 1)

Точки на ободе катка 2 касаются практически неподвижных точек на торце катка 1 и поэтому не двигаются.

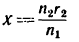
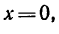
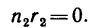
Иначе говоря, если в выражении принять то

Но так как

Задача №2

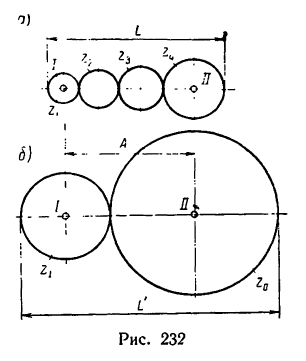
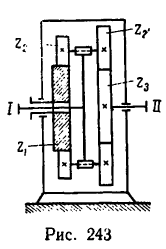
Передача вращательного движения между валами I и II осуществляется при помощи четырех зубчатых колес, два из которых помещены на промежуточных валах (рис. 232, а). Числа зубьев колес:

Модуль зубчатых колес m = 5 мм. Определить передаточное отношение межосевое расстояние А и габариты передачи L. Как изменятся габариты, если передачу осуществить при помощи лишь двух колес того же модуля?

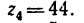
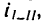
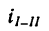
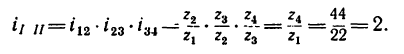
1. Передаточное отношениев данном случае равно произведению трех передаточных отношений между соседними колесами:

Как видно, зубчатые колеса, находящиеся на промежуточных осях, не влияют на величину передаточного отношения; поэтому их иногда называют «паразитными».

2. Находим межосевое расстояние А (см. рис. 232, а):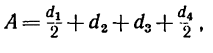

где 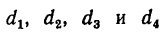— диаметры начальных окружностей зубчатых колес.

Подставляем вместо значений диаметров их выражения через модуль m и соответствующие числа зубьев:

3. Находим габариты передачи L (см. рис. 232, а):

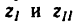
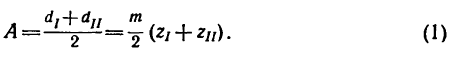
4. Если осуществить передачу при помощи двух колес с числами зубьев того же модуля, оставляя при этом межосевое расстояние передачи неизменным, то оно выразится так (рис. 232, б):

Здесь имеются два неизвестных 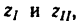но учтя, что передаточное отношение остается неизменным, получаем второе уравнение:

(как уже известно,

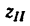
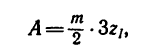
Подставим найденное значение в уравнение (1)

откуда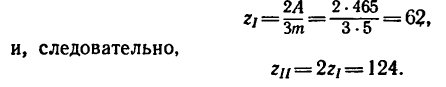

Теперь, зная число зубьев, легко определить габариты двухколесного варианта передачи:

Как видно, габариты увеличиваются на 300 мм, т. е почти в 1,5 раза (на 47,5%).

Отсюда следует сделать вывод, что при значительных межосевых расстояниях, которые по конструктивным причинам нельзя уменьшить, целесообразнее (для уменьшения габаритов) применять рядовое соединение нескольких зубчатых колес.

Задача №3

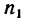
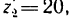
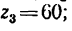
Какую угловую скорость л, нужно сообщить валучтобы при помощи передачи, показанной на рис. 233, вал IV вращался со скоростью —450 об/мин? Числа зубьев колес: коническихцилиндрическогос внутренним зацеплениемдиаметры шкивов

1. Передаточное отношение от вала I к валу IV равно в данном случае произведению трех передаточных отношений:

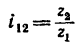
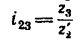
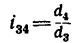
где — передаточное отношение конической зубчатой пары: г,

передаточное отношение цилиндрической пары с внутренним зацеплением;

— передаточное отношение ременной передачи.

После подстановки в эту формулу числовых значений получаем, что угловая скорость первого вала

Задача №4

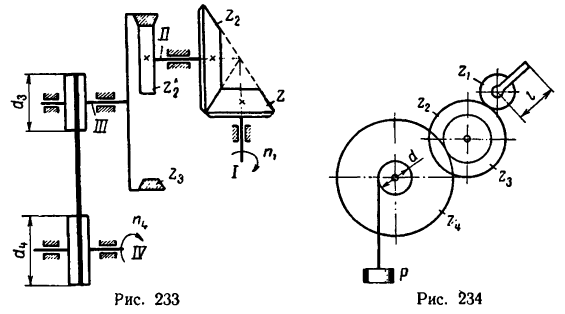
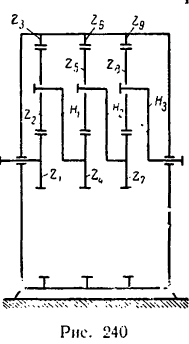
Изображенный на рис. 234 механизм лебедки при вращении рукоятки, имеющей длину I, в вертикальном на-

правлении перемещает груз Р. Диаметр барабана d = 200 мм, число зубьев зубчатых колес механизма:

Определить: 1) с какой скоростью поднимается груз Р, если рукоятка / вращается с угловой скоростью я, =60 об/мин.

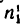
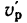
2) угловую скорость рукоятки, если груз должен подниматься со скоростью = 0,2 м/сек.

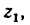
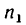
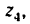
1. Если рукоятка l, жестко соединенная с колесом делает об/мин, то колесо а также жестко соединенный с ним бара бан получают в минуту число оборотов, равное

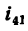
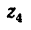
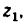
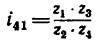
где— передаточное отношение от колеса к колесу причем и, следовательно,

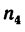
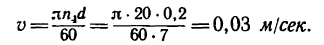
2. Так как барабан, вращаясь, делает об/мин, то окружная скорость точек на поверхности барабана
Скорость подъема груза Р равна окружной скорости и, следовательно,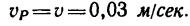

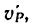
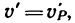
3. Если нужно поднимать груз со скоростью то и барабан должен вращаться так, чтобы его точки двигались с окружной скоростью при этом число оборотов в минуту барабана

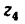
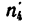
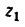
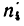
4. Если же барабан и вместе с ним колесо имеют об/мин, то колесо с рукояткой делают об/мин, причем

Такая угловая скорость рукоятки при ручном приводе, конечно, неосуществима.

Следующие две задачи рекомендуется решить самостоятельно.

Определение передаточных отношении простейших планетарных и дифференциальных передач

Планетарными называются передачи, в которых оси одного или нескольких колес закреплены в подвижном звене—водиле.

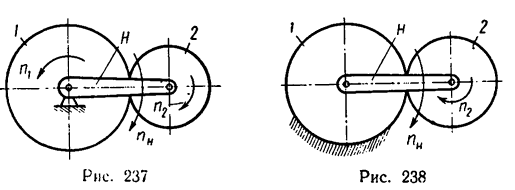
На рис. 237 показана схема передачи, состоящей из нейтрального колеса 1, сателлита 2 и водила H.

В общем случае центральное колесо и водило могут получать вращение от двух источников независимо друг от друга Такая

передача имеет две степени свободы и называется дифференциальной.

Если закрепить центральное колесо, то получается передача с одной степенью свободы — движение можно передавать либо от водила к сателлиту, либо от сателлита к водилу-• такая передача называется простой планетарной (рис. 238).

Чтобы в процессе решения задач глубже проанализировать кинематику планетарных передач, целесообразно не пользоваться готовыми выведенными в учебниках формулами, а применять метод сложения двух движений.

Сателлиты планетарных передач совершают сложное вращательное движение. Движение сателлитов относительно Земли (относительно неподвижной системы координат) складывается из вращения их вместе с водилом — переносного движения и вращения их вокруг осей, закрепленных в водиле, — относительного движения.

Метод сложения двух движений можно распространить и на центральные колеса. Так, например, закрепленное центральное жолесо простой планетарной передачи можно считать вращающимся вместе с воднлом и одновременно поворачивающимся на их общей оси в обратную сторону с такой же скоростью, что и водило.

Поэтому метод, который подробно изложен в решениях задач, включает следующие четыре этапа:

Введем такие обозначения:

-угловые скорости, выраженные в об/мин (рад/сек), зубчатых колес (центральных или сателлитов), дифференциальных передач, индексы соответствуют нумерации колес; — угловая скорость водила в дифференциальной передаче;

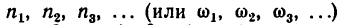
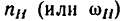
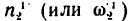
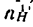
угловые скорости колес или водила в простой планетарной передаче (с закрепленным колесом) обозначим теми же буквами, но с верхними индексами в скобках, соответствующих закрепленному колесу, например— угловая скорость второго колеса при закрепленном первом;— угловая скорость водила при закрепленном первом и т. д.

Аналогично обозначим и передаточные отношения:

При решении задач с планетарными передачами необходимо очень внимательно следить за правильностью определения знаков передаточных отношений между отдельными элементами передачи.

Задача №5

Определить передаточное отношение от сателлита 2 к водилу Н для простой планетарной передачи, показанной на рис. 238, если числа зубьев колес

1. Осуществим первое движение. Закрепим колеса 1 и 2 на водиле и сообщим водилу вместе с колесами вращательное движение с угловой скоростью 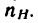Следовательно, в этом движении колеса 1 и 2 также получают угловую скорость

2. Осуществим второе движение. Освободим колеса от водила. Закрепим водило, т. е. превратим простую планетарную передачу в обычную зубчатую передачу, состоящую в данном случае из пары зубчатых колес.

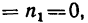
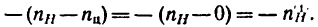
3. Угловая скорость центрального колеса в механизме так как колесо 1 закреплено. Поэтому во втором движении колесу 1 сообщаем скорость

В результате вращения колеса1 колесо 2 приобретет угловую скорость

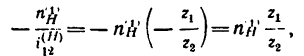
так как передаточное отношение от колеса 1, вращающегося со скоростью

ко второму колесу при закрепленном водиле отрицательное и равно

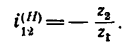
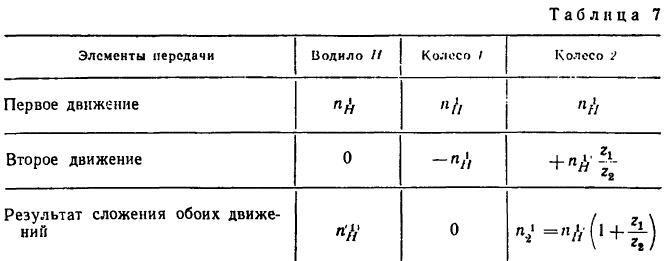
Приведенные результаты заносим в табл. 7, в нижней графе которой затем осуществляем третий этап — сложение обоих значений.

4. Находим передаточное отношение отсателлита 2 к водилу:

Таким образом,

Так как в данном случае передаточное отношение от колеса 2 к колесу 1 при закрепленном водиле имеет отрицательное значение

(a)

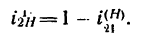
Но при помощи передачи, изображенной на рис. 238, неудобно передавать вращательное движение, так как необходимо дополнительное приспособление, чтобы сообщить угловую скорость сателлиту.

Аналогичная, но несколько видоизмененная простая планетарная передача рассматривается в следующей задаче.

Задача №6

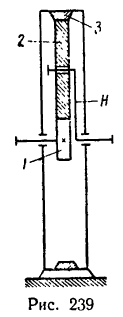
Определить передаточное отношение от колеса 2 к водилу Н простой планетарной передачи с закрепленным колесом внутреннего зацепления (рис. 239), если

1. Так же как и в предыдущей задаче, осуществим сначала первое движение, и тогда все элементы механизма (водило H, колеса 1,. 2 и 3) получат угловую скорость

2. Превратим планетарную передачу в обычную, закрепив водило. Освободим колеса и осуществим

4. Найдем передаточное отношение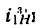

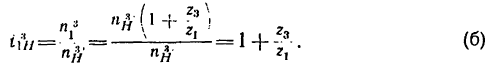
Подставим в (б) числовые значения чисел зубьев:

Таким образом, если к передаче подвести угловую скорость слева (к колесу 1), то справа (у водила Н) угловая скорость уменьшится в шесть раз.

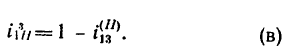
Сравнивая выражение (в) с выражением (а) из предыдущей задачи, замечаем, что они аналогичны.

Как видно, эти передачи не дают большого кинематического эффекта по сравнению с обычными передачами с неподвижными осями: передаточные отношения отличаются только на единицу.

Чтобы увеличить передаточное отношение, передачи, рассмотренные в задаче 202-40, соединяют последовательно.

Задача №7

Определить передаточное отношение 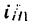для простой планетарной передачи, показанной на рис. 241, если числа зубьев колес

1. Осуществим первое движение (см. табл. 9).

2. Осуществим второе движение при закрепленном водиле, сообщив вращение колесу 3 (см. табл. 9).
3 Записав угловые скорости каждого элемента в первом и втором движении, сложим их (табл. 9).

4. Находим передаточное отношение

Особенно большим получается передаточное отношение, если

близко к единице. Так, например, при

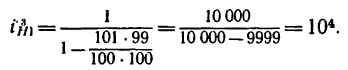
Следовательно, простая планетарная передача, состоящая всего из четырех колес, уменьшает угловую скорость в 10 тысяч раз.

Такие передачи создают большой кинематический эффект, но они имеют и крупный недостаток — крайне низкий коэффициент полезного действия (около 0,5%).

В следующей задаче рассматривается дифференциальная передача.

Задача №8

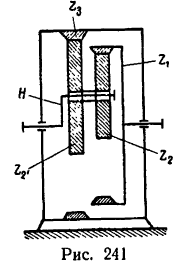
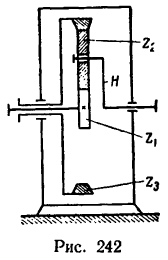
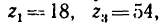
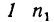
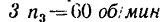
Определить угловую скорость водила Н и колеса 2 дифференциального зубчатого механизма (рис. 242), если число зубьев колес угловая скорость колеса = 120об/мин, угловая скорость колеса при направлении вращения в обратную сторону относительно колеса 1

1 Осуществим первое движение. Закрепив жестко все колеса на водиле, сообщим последнему угловую скорость 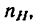тогда все три колеса получат ту же самую угловую скорость.

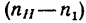
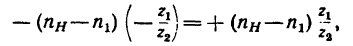
2. Освободив колеса от водила и закрепив его, сообщаем колесу 1 угловую скорость —об/мин. Тогда колесо 2 получит скорость

а колесо 3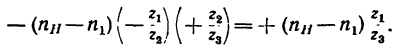

3. Сведем все результаты в табл. 10.

4. Число оборотов в минуту водила найдем из равенства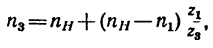

откуда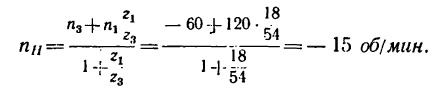

Водило И вращается с угловой скоростью 15 об/мин в ту же сторону, что и колесо 3.

5. Число оборотов в минуту колеса 2 определяем из равенства

но предварительно необходимо определить число зубьев

Из рис. 242 ясно, что

Так как модули всех колес равны между собой, то

откуда

и теперь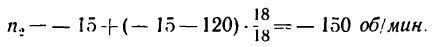
Таким образом, бегающее колесо (сателлит) вращается вокруг своей оси со скоростью 150 об/мин в ту же сторону, что и водило, и колесо 3.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник