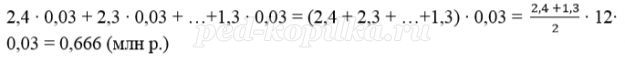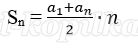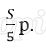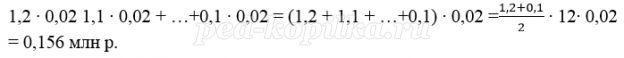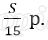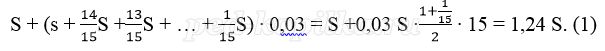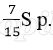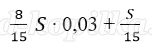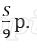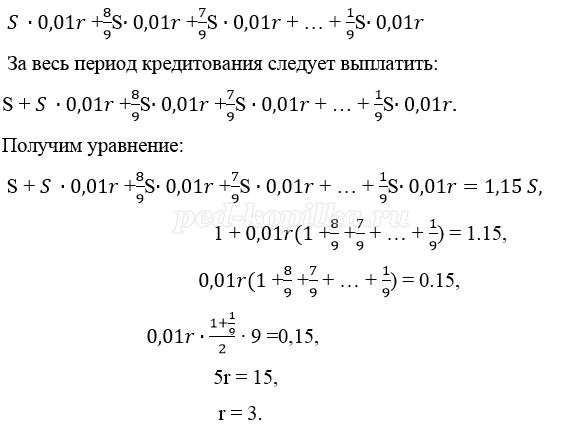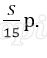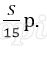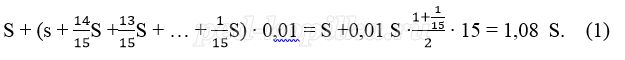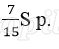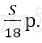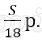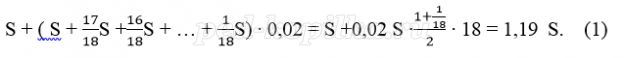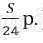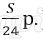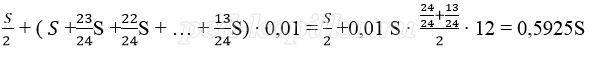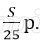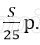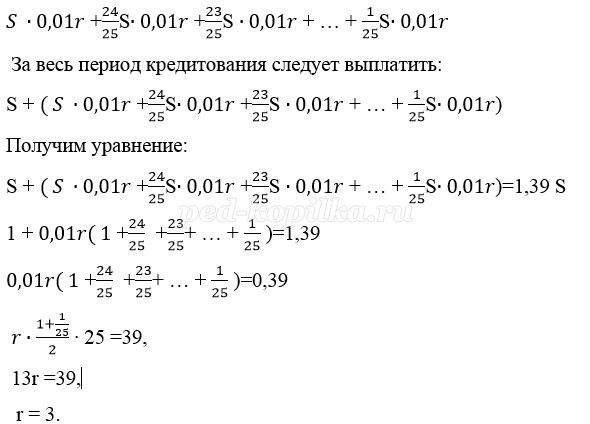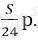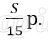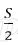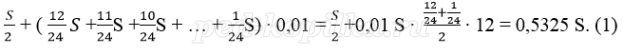задачи на вычисление процентов по кредиту

Задачи на вычисление процентов по кредиту

Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.

Пусть сумма кредита у.е., процентная ставка банка %.

Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Антон взятую сумму возвращал в банк равными долями. Сумма, образованная применением процентной ставки, составляет:

(у.е.)

Общая сумма, выплаченная Антоном за 6 месяцев: (у.е.). А эта сумма по условию задачи равна у.е. Решим уравнение:

«Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину»

«Антон взятую сумму возвращал в банк равными долями.»

При этом решение верное, т.к. для составления формулы использована первая фраза.

S=90тр срок выплаты 3 месяца, ставка 10%

Размер кредита после 1 месяца 99. Что бы сумма долга уменьшалась равномерно (равными долями по 30), первая выплата должна составлять 39

Сумма долга уменьшается равномерно(равными долями по 30тр). Выплаты не равномерны.

Антон, спорить с Антоном по поводу задачи про Антона дело неблагодарное. и всё же

В решении нигде не говорится о том, что выплаты были одинаковыми.

Сказано, что «Антон ВЗЯТУЮ сумму возвращал в банк равными долями.»

В Вашем примере сумму взятую у банка в размере 90тр Антон возвращал равными долями (по 30тр)

Здравствуйте! Необходимо всё это описывать, если пользоваться формулой Дмитрия Гущина?

Если пользоваться формулой Дмитрия Гущина, могут поставить два балла из трех за недостаточное обоснование.

Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна вносить в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2%, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна выплатит банку в течение первого года кредитования?

Пусть B_i — размер долга Жанны на конец месяца i, X_i — платеж Жанны в конце месяца i. Мы знаем, что имеет место соотношение B_i = 1,02B_{i − 1} − X_i. Кроме того, мы знаем, что последовательность (B_i) является арифметической прогрессией. При этом B₀ = 1200 тыс. руб., а B₂₄ = 0, так как в конце срока кредитования долг Жанны должен быть равен нулю. Этих двух точек достаточно, чтобы узнать всю последовательность B_i: Значит,

Поскольку X_i линейно зависит от i, последовательность X_i также является арифметической прогрессией. Значит,

тыс. рублей.

Ответ: 822 тыс. рублей.

Приведём другое решение.

Ежемесячно Жанна возвращает банку по 1,2 млн : 24 = 50 тыс. руб. тела долга и выплачивает равномерно уменьшающуюся от максимального значения до нуля сумму процентов за пользование кредитом. За первый месяц это 0,02 · 1,2 млн = 24 тыс. руб. За второй месяц на 1/24 меньше то есть 23 тыс. руб., затем 22 тыс. руб. и так далее. Поэтому выплаты за 12 первых месяцев составят арифметическую прогрессию с первым членом 74, последним — 63 тыс. руб. Ее сумма равна 12(74 + 63)/2 = 822 тыс. руб.

1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты кредита следующая: 1 марта каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Аркадий переводит в банк платеж. Весь долг Аркадий выплатил за 3 платежа, причем второй платеж оказался в два раза больше первого, а третий – в три раза больше первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку 2 395 800 рублей?

Если первый платеж банку Аркадия составил x рублей, то второй составит 2x рублей, а третий — 3x рублей, всего 6x рублей, что равно 2 395 800, то есть x = 2 395 800 : 6 = 399 300. Отсюда: 2x = 798 600, 3x = 1 197 900.

Пусть в банке Аркадий взял в кредит S рублей.

Тогда его долг 01.03.2011 составил 1,1S рублей. После первого перечисления Аркадия долг снизился до (1,1S − 399 300) руб.

01.03.2012 банк начислил проценты на долг Аркадия. Долг Аркадия стал (1,1S − 399 300) · 1,1 = 1,21S − 439 230 (руб.)

Аркадий перевел в банк 798 600 руб. Долг снизился до 1,21S − 439230 − 798600 = 1,21S − 1237830 (руб.)

01.03.2013 банк начислил проценты на оставшийся долг Аркадия. Долг Аркадия стал (1,21S − 1237830) · 1,1 = 1,331S − 1 361 613 (руб.)

Аркадий перевел в банк 1 197 900 руб. Кредит погашен полностью, долга у Аркадия нет.

Значит, 1,331S − 1 361 613 − 1 197 900 = 0 ⇔ 1,331S = 2 559 513 ⇔ S = 1 923 000.

Ответ: 1 923 000 рублей.

В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

— каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга, равную 69 690 821 рубль.

Сколько рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за три года)?

Если искомая сумма составляет S рублей, то при коэффициенте ежегодной процентной ставки q, равной 1,31, фиксированная сумма которую клиент ежегодно должен возвращать в банк в течение 3 лет, составляет откуда

Заметим, что 69 690 821 кратно Действительно,

Ответ: 124 809 100 рублей.

1. В мировой практике существует и работает два способа (схемы) погашения кредитов: дифференцированная, при которой периодический платеж включает постоянную сумма для погашения основного долга по кредиту, к которой прибавляются проценты на оставшуюся часть долга, и аннуитетная при которой долг гасится равными платежами, как в условии данной задачи.

2. При аннуитетной схеме, как правило, бывает кратным либо фиксированная сумма, которую клиент обязан вносить в отчетный период, либо сумма взятого кредита. Возможен случай, когда та или другая сумма, указанная выше, кратна

3. Прежде чем приступить к решению задачи, лучше проверить ожидаемые кратности, что облегчит дальнейшие вычисления.

Приведём другое решение.

Если искомая сумма составляет x рублей, то:

в начале отчетного периода с учетом возрастания долга

остаток к концу периода после частичного погашения

Ответ: 124 809 100 рублей.

Анатолий решил взять кредит в банке 331000 рублей на 3 месяца под 10% в месяц. Существуют две схемы выплаты кредита.

По первой схеме банк в конце каждого месяца начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Анатолий переводит в банк фиксированную сумму и в результате выплачивает весь долг тремя равными платежами (аннуитетные платежи).

По второй схеме тоже сумма долга в конце каждого месяца увеличивается на 10%, а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину (дифференцированные платежи). Какую схему выгоднее выбрать Анатолию? Сколько рублей будет составлять эта выгода?

Рассмотрим первую схему. Пусть х руб. – искомая фиксированная сумма

Источник

Решение экономических задач на кредиты

Задача 2.
31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5 годовых. Схема выплаты кредита следующая – 31 декабря следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк х рублей. Какой должна быть сумма х, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)?
Решение:
Дмитрий взял в банке кредит 4 290 000 рублей.

При решении задач на кредиты с дифференцированным платежом начисляемые проценты за весь период кредитования можно вычислить с помощью формулы суммы n-первых членов арифметической прогрессии. И потом найти сумму общего платежа. Считаю, что этот метод будет прост и понятен для учащихся.

Задача 3
15 января планируется взять кредит в банке на сумму 2,4 млн. рублей на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Какую сумму надо выплатить банку за первые 12 месяцев?
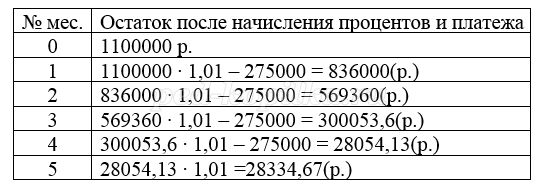
Решение:
Платёж за месяц состоит из величины ежемесячного долга (он равен 2400000:24=100000(р.)) и начисленных к остатку процентов. В каждый месяц долг уменьшается 100000р.
Сумма начисленных «процентов» за 12 месяцев (в млн. р.):

За 12 месяцев буде выплачена половина долга, то есть 1,2 млн р.
Значит за первые 12 месяцев банку нужно выплатить 1 200 000 + 666 000 = 1 866 000 р.
Ответ: 1 866 000 рублей.

Задача 4
15 января планируется взять кредит в банке на 5 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?
Решение:
Пусть в банке взяли кредит S рублей. Платёж за месяц состоит из величины ежемесячного долга (он равен

Всего банку будет выплачено S + 0,03S = 1,03S. Значит общая сумма выплаченных денег от суммы кредита составляет 103%.
Ответ: 103%.

Задача 5
15 января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно выплатить банку за последние 12 месяцев?
Решение:
Платёж за месяц состоит из величины ежемесячного долга (он равен 2400000:24=100000(р.)) и начисленных к остатку процентов. В каждый месяц долг уменьшается 100000р.
Сумма начисленных процентов за 12 последних месяцев (в млн):

За 12 месяцев буде выплачена половина долга, то есть 1,2 млн р.
Значит за последние 12 месяцев банку нужно выплатить 1 200 000 + 156 000 = 1 356 000 р.
Ответ: 1 356 000 рублей.

Задача 6
15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что восьмая выплата составила 99,2 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен

Значит за весь срок кредитования будет выплачено 1 488 000 рублей.
Ответ: 1 488 000 рублей.

Задача 7
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 15% больше, чем сумма взятая в кредит. Найдите r.
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен

Значит кредит взят под 3% в месяц.
Ответ: 3%.

Задача 8
15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что восьмая выплата составила 108 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен

В (1) подставим (2), получим: 1,08 ∙1 500 000 = 1620000
Значит за весь срок кредитования будет выплачено 1 620 000 рублей.
Ответ: 1 620 000 рублей.

Задача 9
15 января планируется взять кредит в банке на 18 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь период кредитования?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен

Значит сумма выплаченных банку денег составляет 119% от суммы долга.
Ответ: 119%.

Задача 10
15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что за первые 12 месяцев нужно выплатить банку 177,75 тыс. рублей. Какую сумму планируется взять в кредит?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен

Получим уравнение: 0,5925 S = 177750,
S = 300000
Значит в кредит взяли 300 000 рублей.
Ответ: 300 000 рублей.

Задача 11
15 января планируется взять кредит в банке на 25 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что я сумма денег, которую нужно выплатить банку за весь срок кредитования, на 39% больше, чем сумма, взятая в кредит. Найдите r.
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен

Значит кредит взят под 3% в месяц.
Ответ: 3%.

Задача 12
15 января планируется взять кредит в банке на 24 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что за последние 12 месяцев нужно выплатить банку 1597,5 тысяч рублей. Какую сумму планируется взять в кредит?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен

Получим уравнение: 0,5325 S = 1597500; S = 3 00 000.
Значит планируется взять 3 000 000 рублей.
Ответ: 3 000 000 рублей.

Литература
И.В.Ященко. Математика. Профильный уровень. Типовые тестовые задания. Издательство «Экзамен», М. 2017.

Источник