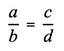задачи по математике 6 класс пропорции и отношения
Задачи по теме «Отношения и пропорции» 6 класс
Ищем педагогов в команду «Инфоурок»
1. Задачи на отношения.
1. Отрезок АВ разделён точкой С на отрезки АС и ВС в отношении 2:7. Найти длину отрезка АВ, если длина отрезка АС на 5,5 см меньше длины отрезка ВС.
2. С двух участков собрали урожай. Каков урожай на каждом участке, если их отношение равно 11:14, а урожай, собранный со второго участка, на 18 тонн больше, чем с первого?
3. Сплав состоит из меди и цинка. Отношение массы меди к массе цинка равно 7:2. Найдите массу сплава, если масса меди на 4кг больше массы цинка в сплаве.
4. Найти массу сплава цинка и меди, если отношение массы меди к массе цинка в сплаве равно 3:5 и меди на 2,4г меньше, чем цинка.
2. Задачи на прямо пропорциональные величины.
1. Из 90 цветов, посаженных в цветнике, принялись 72. На сколько процентов меньше не принявшихся цветов, чем принявшихся?
2. 0,8 м ткани стоят 560 тенге. На сколько больше заплатят за 3,25 м ткани?
3. 4 м 3 зерна ржи весят 2,8 т. На сколько тонн больше весит 6,5 m 3 зерна ржи?
4. Поезд за 4,5 часа проехал 360 км. За какое время, двигаясь с тон же скоростью, поезд проедет расстояние, увеличенное на 80 км?
3. Задачи на обратно пропорциональные величины.
1. Все члены бригады работают в одинаковом темпе. Четверо, рабочих успевают выполнить работу за 32ч. Сколько времени понадобится для выполнения этой же работы трем рабочим?
2. Чтобы вывезти товар потребуется 21 автомашина грузоподъёмностью 2,5 т. Сколько потребовалось бы для выполнения этой работы автомашин грузоподъёмностью 3,5 т?
3. 15 рабочих закончили отделку квартир в новом доме за 24 дня. За сколько дней выполнили бы эту работу 18 рабочих?
4. Пешеход затратил на путь 2,5 ч, двигаясь со скоростью 3,6 км/ч. Сколько времени затратит пешеход на тот же путь, если его скорость будет 4,5 км/ч?
4. Задачи на масштаб.
1. Комната имеет прямоугольную форму. Размеры пола этой комнаты на плане 4см и 6см. В действительности меньшая сторона пола 5 м. Найдите площадь комнаты н масштаб плана.
2. 125 м на местности соответствуют 2,5 см на плане. Найти масштаб плана и расстояние между двумя точками на местности, если на плане оно 4,2 см.
3. План земельного участка квадратной формы выполнен в масштабе 1:500. Сторона участка на плане 16см. Вычисли площадь участка.
4. На карте расстояние между годами А и В равно 2,6см. а расстояние между городами В и С – 3,7см, На местности расстояние между- городами В и С равно 296км. Найдите расстояние на местности между годами А и В и масштаб карты.
Подборка прикладных задач по теме «Отношения. Масштаб. Пропорции.»
Ищем педагогов в команду «Инфоурок»
Отношения чисел и величин. Масштаб.
Задача №1. Расстояние на карте между двумя пунктами составляет 4,3 см. Каково расстояние между этими пунктами на местности, если масштаб карты равен 1 : 300 000?
Задача №2. Расстояние между двумя пунктами на местности равно 140 км. Каково расстояние между ними на карте, масштаб которой равен 1 : 2 000 000?
Задача №3. Расстояние между двумя пунктами на местности равно 216 км, а на карте — 5,4 см. Найдите масштаб карты.
Задача №4. Расстояние на карте между двумя городами равно 2,3 см. Каково расстояние между этими городами на местности, если масштаб карты равен 1 : 200 000?
Задача №5. Расстояние между двумя городами на местности равно 320 км. Каково расстояние между ними на карте, масштаб которой равен 1 : 8 000 000?
Задача №6. Расстояние между двумя пунктами на местности равно 195 км, а на карте — 6,5 см. Найдите масштаб карты.
Задача №7. Из 300 кг семян льна получают 144 кг масла. Сколько масла получат из 225 кг семян льна? Сколько семян льна требуется, чтобы получить 420 кг масла?
Задача №8. Площадь поля равна 520 га. За первый день собрали урожай с 15 % площади поля. С какой площади (в гектарах) собрали урожай?
Задача №9. Расстояние между городами А и В на карте равно 4,8 см, а на местности — 120 км. Каково расстояние между городами C и D на этой карте, если расстояние между ними на местности равно 160 км?
Задача №10. В 400 кг сплава содержится 176 кг меди. Сколько килограммов меди содержится в 325 кг сплава? Найдите массу сплава, если в нём содержится 308 кг меди.
Задача №11. Строители должны были проложить 480 м путепровода. За первую неделю они выполнили 35 % работы. Сколько метров путепровода проложили строители за первую неделю?
Задача №12. Расстояние между сёлами М и К на карте равно 5 см 6 мм, а на местности — 420 км. Каково расстояние между сёлами С и D на местности, если на этой карте расстояние между ними равно 3 см 6 мм?
Задачи на составление пропорций (6 класс)
В данном материале размещены (подобраны) 38 задач на составление и решение пропорций. Данную разработку удобно использовать для уроков практикумов по данной теме
Просмотр содержимого документа
«Задачи на составление пропорций (6 класс)»
Задачи на проценты (урок практикум)
В дачный поселок проводили газ. За 45 дней 32 жителя поселка вручную вырыли траншею для труб. Сколько бы понадобилось времени для рытья такой же траншеи 24 жителям поселка?
За 5кг товара заплатили 325руб. Вычисли стоимость 11кг этого товара.
16солдат могут открыть окоп за 21ч. Сколько понадобится солдат, чтобы выполнить эту работу за 12ч?
Толщина 300 листов бумаги для принтера составляет 3, 3 см. Какую толщину будет иметь пачка из 500 листов такой же бумаги?
Сколько воды содержится в 5 кг арбуза, если известно, что арбуз состоит на 98% из воды?
Масса 21 литра нефти составляет 16,8 кг. Какова масса 35 литров нефти?
После того, как было вспахано 82% всего поля, осталось вспахать еще 9 га. Какова площадь всего поля?
Масса 15 одинаковых деталей составила 37,5кг. Какова масса 12 таких деталей?
Из 9,6кг помидоров можно получить 4л томатного соуса. Сколько литров соуса можно получить из 84кг помидоров?
Из 9,6кг помидоров можно получить 4л томатного соуса. Сколько килограммов помидоров необходимо для приготовления 24л соуса?
24 человека за 6 дней пропололи участок клубники. За сколько дней выполнят ту же работу 36 человек, если будут работать с такой же производительностью.
На пошив 9 рубашек ушло 18,9м ткани. Сколько метров ткани уйдёт на пошив 12 таких рубашек?
На пошив 9 рубашек ушло 18,9м ткани. Сколько рубашек можно пошить из 44, 1м ткани?
Бригада из 8 рабочих выполняет задание за 12 дней. За сколько дней выполнят задание, если рабочих сократят до 6?
Бригада из 8 рабочих выполняет задание за 12 дней. Сколько рабочих выполнят задание за 8 дней?
На 30га пашни было посеяно 5,4т овса. Сколько зерна потребуется для засева 2060га пашни.
За несколько одинаковых карандашей заплатили 8 р. Сколько нужно заплатить за такие же карандаши, если их купили в 2 раза меньше?
За несколько одинаковых карандашей заплатили 8 р. Сколько нужно заплатить за такое же количество карандашей, каждый из которых в 2 раза дороже?
Имеются деньги на покупку 30 карандашей. Сколько тетрадей можно купить на те же деньги, если тетрадь дешевле карандаша в 2 раза?
Велосипедист за несколько часов проехал 36 км. Какое расстояние пройдет за то же время пешеход, скорость которого в 3 раза меньше скорости велосипедиста?
Некоторое расстояние велосипедист проехал за 3 ч. За сколько часов это расстояние проедет мотоциклист, скорость которого в 5 раз больше скорости велосипедиста?
За 6 ч поезд прошел 480 км. Какой путь прошел поезд за первые 2 ч, если его скорость была постоянна?
Для варки варенья из вишни на 6 кг ягод берут 4 кг сахарного песку. Сколько килограммов сахарного песку надо взять на 12 кг ягод?
В 100 г раствора содержится 4 г соли. Сколько граммов соли содержится в 300 г раствора?
Расстояние между двумя городами пассажирский поезд прошел со скоростью 80 км/ч за 3 ч. За сколько часов товарный поезд пройдет то же расстояние со скоростью 40 км/ч?
Пять маляров могли бы покрасить забор за 8 дней. За сколько дней покрасят тот же забор 10 маляров?
За 2 ч поймали 12 карасей. Сколько карасей поймают за 3 ч?
Что такое пропорция
Что такое пропорция
Пропорция — это равенство двух отношения.
Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.
Пропорция всегда содержит равные коэффициенты.
Если выразить определение формулой, то выглядеть оно будет так:
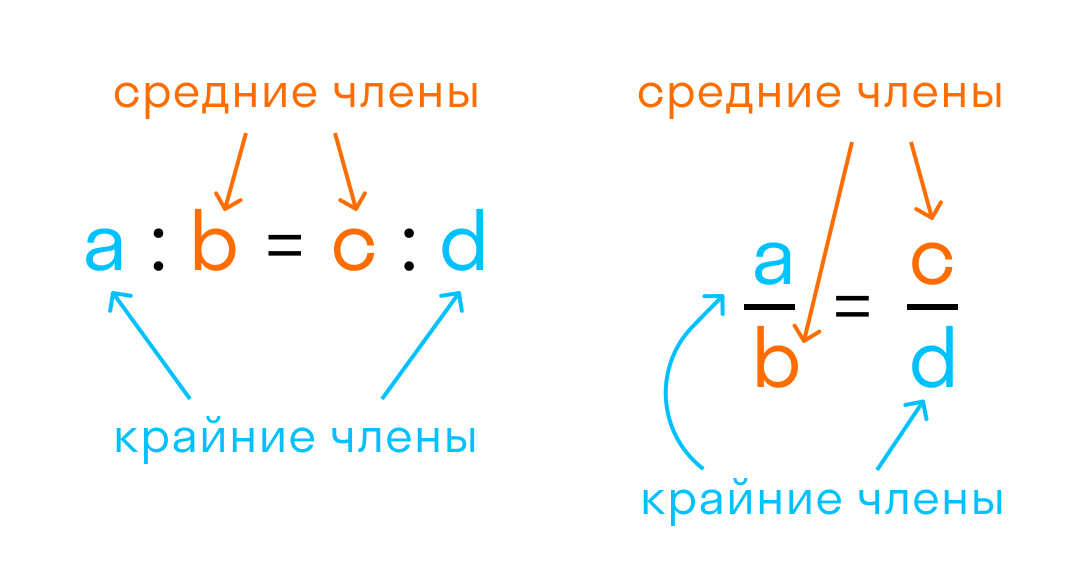
a и d — крайние члены пропорции
Читается это выражение так: a так относится к b, как c относится к d
Например:
Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.
15 и 3 — крайние члены пропорции.
5 и 9 — средние члены пропорции.
Наглядный пример для понимания:
У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.
Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!
А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.
Что мы имеем: 4 кусочка и 2 друга, претендующих на них.
Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.
Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.
Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным😉
Основное свойство пропорции
Запомните основное свойство пропорции:
Произведение крайних членов пропорции равно произведению средних членов этой пропорции.
В виде формулы свойство выглядит так:
a : b = c : d = a * d = b * c
Мы знаем, что a и d — крайние члены пропорции, b и c — средние.
Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.
Давайте проверим несколько пропорций.
Пример 1. Дана пропорция:6/2 = 12/4
Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.
Пример 2. Дана пропорция: 10/2 = 16/4
Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.
Примеры решения задач с пропорцией
Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.
Задачка 1. Дана математическая пропорция: 15/3 = x/4
Ответ: в пропорции 15/3 = x/4, x = 20
Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.
Ответ: четвертый член пропорции — 12.
Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?
Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.
Задачка 4. Дана пропорция: 20/2 = y/4
Задачи на пропорции
5 класс, 7 класс, 8 класс
Понятие пропорции
Чтобы решать задачи на тему пропорции, вспомним главное определение.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин.
Главное свойство пропорции:
Произведение крайних членов равно произведению средних.
где a, b, c, d — члены пропорции, a, d — крайние члены, b, c — средние члены.
Вывод из главного свойства пропорции:
Решить пропорцию — значит найти неизвестный член. Свойство пропорции — главный помощник в решении.
Рассмотрим легкие и сложные задачи, которые можно решить с помощью пропорции. 5, 6, 7, 8 класс — неважно, всем школьникам полезно проанализировать занимательные задачки.
Задачи на пропорции с решением и ответами
Свойства пропорции придумали не просто так! С их помощью можно найти любой из членов пропорции, если он неизвестен. Решим 10 задач на пропорцию.
Задание 1. Найти неизвестный член пропорции: x/2 = 3/1
В этом примере неизвестны крайние члены, поэтому умножим средние члены и разделим полученный результат на известный крайний член:
Задание 2. Найти неизвестный член: 1/3 = 5/y
Задача 3. Решить пропорцию: 30/x = 5/8
Задание 4. Решить: 7/5 = y/10
Задание 5. Известно, что 21x = 14y. Найти отношение x — к y
На следующем примере мы узнаем как составить пропорцию по задаче💡
Задание 6. Из 300 подписчиков в инстаграм 108 человек — поставили лайк под постом. Какой процент всех подписчиков составляют те, кому понравился пост и они поставили лайк?
Ответ: 36% всех подписчиков поставили лайк под постом.
Задание 7. Подруга Гарри Поттера при варке оборотного зелья использовала водоросли и пиявки в отношении 5 к 2. Сколько нужно водорослей, если есть только 450 грамм пиявок?
Ответ: на 450 грамм пиявок нужно взять 1125 гр водорослей.
Задание 8. Известно, что арбуз состоит на 98% из воды. Сколько воды в 5 кг арбуза?
Вес арбуза (5 кг) составляет 100%. Вода — 98% или х кг.
Ответ: в 5 кг арбуза содержится 4,9 кг воды.
Перейдем к примерам посложнее. Рассмотрим задачу на пропорции из учебника по алгебре за 8 класс.
Задание 9. Папин автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
Соотношения равны, но перевернуты относительно друг друга.
t2 = (75 * 13)/52 = 75/4 = 18 3/4 = 18 ч 45 мин
Ответ: 18 часов 45 минут.
Задание 10. 24 человека за 5 дней раскрутили канал в телеграм. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.
3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так: