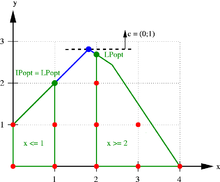
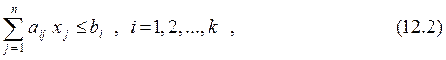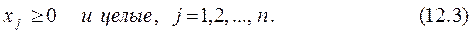задачу целочисленной оптимизации часто можно представить и в геометрической и в форме
Задачу целочисленной оптимизации часто можно представить и в геометрической и в форме
13. ЦЕЛОЧИСЛЕННОЕ ПРОГРАММИРОВАНИЕ
Целочисленное программирование – один из наиболее молодых, перспективных и быстро развивающихся разделов математического программирования. Можно перечислить большое количество разнообразных задач планирования экономики, организации производства, исследования конфликтных ситуаций, синтеза схем автоматического регулирования, которые формально сводятся к выбору лучших, в некотором смысле, значений параметров из определенной дискретной совокупности заданных величин. К ним можно отнести и экстремальные комбинаторные задачи, возникающие в различных разделах дискретной математики.
Задачи и методы, относящиеся к перечисленному кругу вопросов, в литературе именуются по-разному. Наибольшее распространение получил термин «целочисленное программирование», однако встречаются и такие как «дискретное программирование», реже «комбинаторное (или диофантово) программирование».
Наиболее изученными задачами этого класса являются целочисленные задачи линейного программирования, в которых на все переменные (или на их часть) наложено дополнительное требование целочисленности. От них принято отличать так называемые дискретные задачи линейного программирования, в которых область допустимого изменения каждой переменной – не множество целых неотрицательных чисел, а некоторое заданное конечное множество.
Целочисленные задачи математического программирования могут возникать различными путями.
1. Существуют задачи линейного программирования, которые формально к целочисленным не относятся, но при соответствующих исходных данных всегда обладают целочисленным планом. Примеры таких задач – транспортная задача и ее модификации (задачи о назначениях, о потоках в сетях).
2. Толчком к изучению целочисленных задач в собственном смысле слова явилось рассмотрение задач линейного программирования, в которых переменные представляли физически неделимые величины. Они были названы задачами с неделимостью. Таковы, например, задачи об оптимизации комплекса средств доставки грузов, о нахождении минимального порожнего пробега автомобилей при выполнении заданного плана перевозок, об определении оптимального машинного парка и его оптимального распределения по указанным работам при условии минимизации суммарной стоимости (машинного парка и производимых работ), о нахождении минимального количества судов для осуществления данного графика перевозок и т. п.
3. Другим важным толчком к построению теории целочисленного программирования стал новый подход к некоторым экстремальным комбинаторным задачам. В них требуется найти экстремум целочисленной линейной функции, заданной на конечном множестве элементов. Такие задачи принято называть задачами с альтернативными переменными. В качестве примеров можно назвать задачи коммивояжера (бродячего торговца), об оптимальном назначении, теории расписания, или календарного планирования, и задачи с дополнительными логическими условиями (например, типа «или – или», «если – то» и т. п.).
Исторически первой задачей целочисленного типа является опубликованная в 1932 г. венгерским математиком Е. Эгервари задача о назначении персонала. В 1955 г. на Втором симпозиуме по линейному программированию была рассмотрена задача о бомбардировщике, известная как задача о ранце.
Приведем примеры целочисленных задач линейного программирования.
Составим математическую модель задачи. Обозначим через 


Сопоставление расходов ресурсов каждого типа для транспортировки единицы груза и их наличия приводит к ограничению

Общая полезность рейса определяется значением функции

Частным случаем задачи (13.1) – (13.2) является задача о ранце, в которой любой из заданного набора предметов 
найти максимум функции 
Несостоятельность округления подчеркивается также следующими соображениями. Несмотря на то, что целочисленные переменные обычно выражают количество неделимых предметов, возможны и другие типы спецификации этих переменных. Так в задаче о ранце решение представляется булевой переменной 
Из приведенного примера видно, что для решения задач целочисленного программирования необходимо рассмотреть особые методы оптимизации. Кроме того, оптимальное решение задач целочисленного программирования не обязательно принадлежит границе многогранника (многоугольника) условий, что характерно для задач линейного программирования.
Целочисленная линейная оптимизация
Содержание
Определение проблемы
Математическая формулировка
Геометрическая интерпретация
Целочисленную оптимизацию, как и линейный вариант, можно в значительной степени интерпретировать геометрически. Количество
называется ЛП-релаксацией целочисленной задачи и играет важную роль в некоторых методах решения (см. ниже ).
Примеры
На картинке напротив изображена целочисленная линейная программа
Следующий IP-адрес является примером упомянутого выше особого случая:
Приложения
Целочисленные условия значительно расширяют возможности моделирования практических задач по сравнению с линейной оптимизацией. Есть две основные причины использования целочисленных переменных:
Часто оба случая встречаются вместе. Целочисленная оптимизация может использоваться во многих практических областях применения, некоторые из которых кратко описаны ниже.
Производственное планирование
Местный общественный транспорт
При планировании услуг и транспортных средств в общественном транспорте речь идет, например, об автобусах или метро, чтобы распределить отдельные линии, которые могут быть соблюдены в расписании, и оборудовать их водителями. Здесь важную роль играют двоичные переменные решения. B. Выразить, ездит ли по линии автобус определенного типа или нет, и назначен ли машинист метро к определенному поезду или нет.
Телекоммуникационные сети
Целью планирования пропускной способности и маршрутизации в общенациональных сетях электросвязи является установка пропускной способности на узлах и линиях сети и маршрутизация требований к связи таким образом, чтобы все требования были удовлетворены, а общие затраты сети были минимальными. Как правило, емкость не может быть установлена в произвольных пропорциях, а только в определенных целочисленных единицах. В зависимости от используемой технологии обычно существуют другие ограничения, которые можно моделировать как линейные неравенства с целочисленными или двоичными переменными.
Сотовые сети
Задача частотного планирования в сетях мобильной радиосвязи GSM состоит в том, чтобы распределить доступные частоты по антеннам таким образом, чтобы можно было обслуживать всех пользователей и свести к минимуму мешающие помехи между антеннами. Эта задача может быть сформулирована как целочисленная линейная программа, в которой u. а. Двоичные переменные показывают, назначена ли частота конкретной антенне.
Планирование тура
0/1 программирование
сказка
Сложность и способ решения
Точные и эвристические процедуры
При классификации алгоритмов необходимо различать точные и эвристические методы решения.
Двойные оценки и доказательство оптимальности
В ходе алгоритма ослабление постепенно усиливается (например, путем добавления дополнительных неравенств), так что результирующая верхняя граница становится все меньше и меньше. В то же время делается попытка найти более приемлемые решения для повышения нижней границы. Это показано на следующем рисунке. Если значение найденного решения и двойственная оценка совпадают (в примере со значением 2), это доказывает, что найденное решение является оптимальным.
Далее более подробно представлены некоторые важные точные и эвристические методы решения.
Метод резки плоскости
Ветвь-и-граница или ветвь-и-разрез
Также ветвление и граница начинается с высвобождения релаксации ЛП. Если полученное решение не является целым числом, проблема разбивается на две или более подзадач таким образом, что каждое возможное решение содержится в одной из этих подзадач. Таким образом, дерево ветвей строится с релаксацией LP в качестве корневого узла. (В каждой ветке английской ветки диапазон значений одной или нескольких переменных) регионов. Это делается до тех пор, пока не будет найдено лучшее целочисленное решение.
Релаксация Лагранжа
Решение этой более простой проблемы в большинстве случаев не будет отвечать условиям, ослабленным в целевой функции. Чтобы изменить это, множители Лагранжа корректируются с помощью метода субградиента в зависимости от текущего (недопустимого) решения, так что новое решение с новыми весами генерирует несколько «более допустимое» решение, которое менее серьезно нарушает ослабленные неравенства. Этот процесс повторяется итеративно, пока не будут выполнены все условия. Можно показать, что каждое решение релаксации Лагранжа дает двойную оценку для исходного IP, и что этот метод сходится с подходящей настройкой множителей.
Эвристика
Почти для каждой задачи оптимизации легко найти множество эвристик, которые быстро найдут допустимые решения для этой конкретной проблемы. Напротив, разработка эвристических методов, которые надежно находят хорошие решения, и, если возможно, также для целого класса связанных задач оптимизации, а не только для конкретной проблемы, является нетривиальной задачей.
Как единственный метод решения, все эти алгоритмы имеют тот недостаток, что, во-первых, они не всегда находят решение, а во-вторых, в большинстве случаев ничего не известно о качестве найденных решений по сравнению с оптимальным решением. Однако их можно, например, очень разумно использовать как часть подхода ветвей и отсечений, чтобы генерировать хорошие допустимые решения в различных узлах в дереве поиска, например, из текущего решения LP, и, таким образом, иметь возможность отрезать части дерева.
Сущность целочисленной оптимизации (целочисленного линейного программирования (ЦЛП))



Основные понятия и определения
В ЗАДАЧАХ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ
Задачи целочисленной оптимизации. Частично целочисленные задачи. Дихотомические решения. Зависимые решения.
При решении многих оптимизационных задач требуется, чтобы компоненты вектора неизвестных 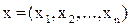
Если требование целочисленности распространяется лишь на часть переменных, то задача называется частично целочисленной.
Задачи этого типа представляют отдельную область оптимизационного моделирования. Их роль в моделях принятия решений определяется тем, что они позволяют проводить выбор альтернатив для проблем высокой сложности.
Иногда решения задач ЦЛП получают, округляя результаты решений обычных задач линейного программирования. Например, если оптимальное число производимых станков крупным промышленным предприятием оказалось равным 3200,2, то в качестве оптимального решения соответствующей задачи целочисленной оптимизации берется округленное значение 3200.
Этот простой способ плохо работает при малых значениях переменных. Если решение обычной задачи линейной оптимизации предлагает произвести 3,6 крупных транспортных корабля класса А и 4,8 класса В, то округление этих значений до 4 и 5 соответственно может привести к нарушению ограничения по ресурсам.
Целочисленность переменных существенно усложняет поиск оптимальных решений в случае большого числа переменных. Оптимизация моделей ЦЛП требует на 1-3 порядка больших затрат машинного времени по сравнению с задачами ЛП с тем же количеством переменных. Это связано с тем, что при решении задачи симплекс-методом решение ищется лишь в соответствующих вершинах многогранников, определяющих область допустимых решений (метод обхода), тогда как алгоритм решения задач ЦЛП требует расчета в гораздо большем числе точек. Это иллюстрируется рисунком, изображающим двумерную задачу; область допустимых решений (ОДР) схематически изображена затемненным пятиугольником.
Метод полного перебора (т.е. расчет значений ЦФ во всей области допустимых решений и выбор точки, соответствующей оптимальному значению) для большинства практических задач нереализуем. В случае, когда модель ЦЛП содержит 20 переменных, каждая из которых может принимать целые значения от 1 до 50, полный перебор требует провести 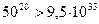
Во многих моделях ЦЛП переменные могут принимать только значения 0 или 1 (модели двоичного целочисленного линейного программирования). Эти модели особенно важны для ТПР, так как двоичные переменные можно использовать для представления дихотомических решений (решений типа “да – нет”). К этому классу задач принадлежат модели назначений, размещения производственных объектов и офисов, производственного планирования и управления инвестиционными портфелями.
Приведем два простых примера.
В модели размещения производственных объектов 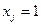

В модели маршрутизации 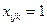
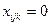
О ЦЕЛОЧИСЛЕННОЙ ОПТИМИЗАЦИИ В ЭКОНОМИЧЕСКИХ ЗАДАЧАХ
Постановка проблемы. Задачи целочисленной оптимизации возникают в различных теоретических и практических исследованиях, поэтому и вызывают особый интерес у экономистов. Важно понимать алгоритм решения данных задач, чтобы делать правильные прогнозы относительно различных производственных показателей, построения оптимальных маршрутов, максимизации прибыли и минимизации издержек в условиях целочисленности переменных.
Актуальность данного исследования обусловлена тем, что на практике часто встречаются проекты, которые нельзя реализовать по частям. Кроме того, сами объекты производства или инвестирования могут не подлежать дроблению (например, здания, персонал и др.). В этих случаях целесообразно воспользоваться методологией целочисленной оптимизации.
Анализ достижений и публикаций. Проблемам целочисленности оптимизации уделяли внимание такие учёные как В.В.Леонтьев, Л.В.Канторович, И.И.Дикин, А.М.Семахин и др. Из зарубежных учёных наиболее известен Р.Гомори, который в 1958 г. предложил метод отсечения плоскостей [1, с. 132-147], [2, гл. 9]. Современные исследователи [3] тоже уделяют внимание проблемам целочисленной оптимизации.
Основная часть. Рассмотрим задачи целочисленности линейной оптимизации (ЦЛО), когда целевая функция и ограничения являются линейными. Математическая модель ЦЛО такая же, как и задача линейной оптимизации, но с дополнительным требованием целочисленности всех или части неизвестных. Если требование целочисленности распространяется на часть неизвестных величин задачи, то такая задача называется частично целочисленной.
Запишем математическую модель задачи ЦЛО. Требуется найти экстремальное значение целевой функции


Задачи целочисленной оптимизации решаются методом Гомори, методом ветвей и границ, которые реализованы при помощи информационных технологий. Рассмотрим вышеперечисленные методы.
Метод Гомори основан на применении симплекс-метода и метода отсечения. Сначала находится оптимальное решение задачи ЦЛО симплекс-методом, и если целочисленное решение получено, то цель достигнута. Если же оптимальное решение не является целочисленным, то в условия задачи вводится дополнительное ограничение, которое отсекает от области допустимых решений полученное решение и не отсекает от неё ни одной точки с целочисленными координатами. Далее симплекс-методом решается расширенная задача. Если новое решение не будет целочисленным, то вводится ещё одно дополнительное ограничение, и процесс повторяется до тех пор, пока не будет найдено оптимальное целочисленное решение, или не будет установлено, что его не существует. Геометрическая иллюстрация метода Гомори осуществляется с помощью графического поля, на которое нанесена целочисленная сетка.
Рассмотрим метод ветвей и границ. Суть данного метода и технология его применения заключаются в том, что сначала в области допустимых решений (ОДР) системы ограничений находится оптимальное решение задачи симплекс-методом без учёта условия целочисленности. Если в полученном решении некоторые переменные имеют дробные значения, то выбираем любую из дробных переменных и по ней строим два ограничения. В одном ограничении величина переменной будет меньше или равна наибольшему целому числу, не превышающему значения дробной переменной в оптимальном решении, а в другом ограничении она больше или равна наименьшему целому значению, но не меньше значения дробной переменной. В результате разбиения ОДР будут получены две новые задачи (подзадачи). Если после их решения полученные значения неизвестных не будут целочисленные, то, сравнив значения целевых функций этих задач, выбираем задачу с большим значением функции и по новой неизвестной с дробным значением строим снова два дополнительных ограничения. В результате получим ветви. Ветвление заканчивается нахождением целочисленного решения, если оно существует.
Особый интерес представляет собой способ решения задачи целочисленной оптимизации средствами Excel. Приведём пример такой задачи и решим её при помощи информационных технологий.
Морское судно грузоподъёмностью 20 тыс. т. и вместимостью 28 тыс. м 3 может быть использовано для перевозки пяти видов груза. Данные о массе, объёме и стоимости единицы груза приведены в табл. 1.
| Параметры единицы груза | Номер груза |
| Масса, т | |
| Объём, м 3 | |
| Стоимость, тыс. руб. |
Требуется определить, сколько единиц груза каждого вида следует загрузить на судно, чтобы суммарная стоимость груза была максимальной и выполнялись ограничения по вместимости и грузоподъёмности судна.
Составим математическую модель данной задачи:



Решение данной задачи осуществляется командой «Поиск решения» из меню «Сервис». Далее в форму представления данных вносят всё необходимое [1, с. 142-145]. Закончив ввод ограничений, командой «Добавить» вводят условия целочисленности. Для этого в диалоговом окне «Добавление ограничения» вводят в окно ссылку на ячейку адреса, где должны быть изменяемые значения неизвестных.
Таким образом, проведя вычисление при помощи Excel, получим оптимальный план и экстремальное значение целевой функции:


Подведение итогов. В данном исследовании проведен анализ целочисленной оптимизации в экономических задачах, рассмотрены основные методы решения данных задач – метод Гомори, метод ветвей и границ, использование программного обеспечения Excel, обоснована необходимость применения каждого из методов. Таким образом, можно сделать вывод, о том, что задачи целочисленной оптимизации имеют практическую направленность, их решение обеспечивает максимизацию или минимизацию при условии целочисленности переменных.
Литература:
5. Костевич Л.С. Математическое программирование: информационные технологии оптимальных решений: [учеб. пособие] / Л.С.Костевич. – Мн.: Новое знание, 2003. – 424 с.: ил. – Библиогр.: с. 419. – ISBN 985-6516-83-8.
6. Таха Х.А. Введение в исследование операций, 7-е издание.: Пер. с англ. / Х.А.Таха. – М.: Издательский дом «Вильямс», 2005. – 912 с.: ил. – ISBN 5-8459-0740-3 (рус.).
7. Полшков Ю.Н. О современных подходах экономико-математического моделирования в маркетинге // Вiсник Донецького національного унiверситету. Серiя В. Економiка i право. Спецвипуск, том 2. – Донецьк: ДонНУ, 2012. – С. 199-207.