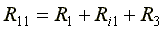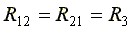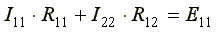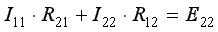законы теории электрических цепей в матричной форме с примерами моделирования с помощью matlab
MATLAB. KursRab. Расчёт и моделирование электрической цепи
После лабораторных работ (Решение систем линейных алгебраических уравнений, Методы численного интегрирования, Численное дифференцирование функций, Приближенные методы решения обыкновенных дифференциальных уравнений, Аппроксимация функций) часто следует курсовая работа. В последнее время я ничего не публиковал из университетских работ. Но я не бездельничал — в курсовой работе много графиков, формул и таблиц…
СОДЕРЖАНИЕ
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ
Задачей данной курсовой работы является практическое применение методов вычислительной математики для расчёта электрической цепи.
Задание.
Рассчитать выбранную согласно варианту электрическую схему (см. «Варианты электрических цепей») тремя способами. Провести анализ полученных результатов.
Расчёт необходимо произвести следующими способами:
Выбор методики расчёта:
Формулы для вычисления индивидуального задания:
№ электрической схемы=(№ студента по списку + 2*(№ группы-40)) mod 16+1
№ метода решения системы уравнений =№ студента по списку mod 5+1
№ метода вычисления определителя =№ студента по списку mod 2+1
№ метода вычисления обратной матрицы=№ студента по списку mod 2+1
Согласно этим формулам:
№ электрической схемы=(13 + 2*(42-40)) mod 16+1=(13+2*2) mod 16+1=17 mod 16 +1=1+1=2.
№ метода решения системы уравнений = 13 mod 5+1=3+1=4
№ метода вычисления определителя =13 mod 2+1=1+1=2
№ метода вычисления обратной матрицы=13 mod 2+1=1+1=2
Метод решения системы уравнений:
Метод вычисления определителей:
По определению: с использованием алгебраических дополнений
Метод вычисления обратной матрицы:
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ПО ВЫБРАННОМУ МЕТОДУ РАСЧЁТА ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
При расчёте электрических цепей используются два закона Кирхгофа.
Первый закон Кирхгофа, или закон Кирхгофа для узлов:
Сумма токов, расходящихся от узла электрической цепи, равна нулю.
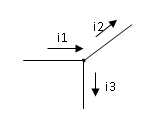
При составлении уравнений согласно первому закону Кирхгофа необходимо задаться условно-положительными направлениями токов во всех ветвях, обозначив их на схеме стрелками. В левой части уравнения следует ставить знак «плюс» перед буквенными обозначениями токов, положительное направление которых принято от узла, и знак «минус» перед буквенными обозначениями токов, положительное направление которых принято к узлу. Для случая, представленного на рисунке следует написать:
Если в результате расчёта будет получено для некоторого тока в некоторый момент времени положительное число, то это значит, что ток имеет в данный момент времени действительное направление согласно стрелке. Если же будет получено отрицательное значение, то этот тот в действительности направлен против стрелки.
Второй закон Кирхгофа, или закон Кирхгофа для контуров.
Сумма падений напряжения во всех ветвях любого замкнутого контура электрической цепи равна сумме ЭДС источников энергии, действующих в этом контуре.
Для составления уравнений согласно второму закону Кирхгофа должны быть заданы положительные направления токов ik и ЭДС ek источников энергии во всех ветвях.
Метод непосредственного применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество совместно решаемых уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа.
Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.
На рисунке в качестве примера изображена двухконтурная схема, в которой I11 и I22 — контурные токи.
Токи в сопротивлениях R1 и R2 равны соответствующим контурным токам. Ток в сопротивлении R3, являющийся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви с R3 встречно.
Выбираются независимые контуры, и задаются произвольные направления контурных токов.
В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:
Перегруппируем слагаемые в уравнениях
Суммарное сопротивление данного контура называется собственным сопротивлением контура.
Собственные сопротивления контуров схемы
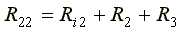
где R12 — общее сопротивление между первым и вторым контурами;
R21 — общее сопротивление между вторым и первым контурами.
E11 = E1 и E22 = E2 — контурные ЭДС.
В общем виде уравнения (4.4) и (4.5) записываются следующим образом:
Собственные сопротивления всегда имеют знак «плюс».
Общее сопротивление имеет знак «минус», если в данном сопротивлении контурные токи направлены встречно друг другу, и знак «плюс», если контурные токи в общем сопротивлении совпадают по направлению.
Решая уравнения (1) и (2) совместно, определим контурные токи I11 и I22, затем от контурных токов переходим к токам в ветвях.
Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви.
УТОЧНЕНИЕ ЗАДАНИЯ:
В силу специфики итерационного метода Гаусса-Зейделя система составленная система уравнений может не сойтись. Скорее всего система уравнений, составленная просто применением законов Кирхгофа не сойдётся, так как в уравнениях, составленных для узлов системы модули диагональных коэффициентов будут либо равны нулю, либо единице. Но и в том и в другом случае они будут меньше сумм модулей всех остальных коэффициентов. Следовательно, метод Гаусса-Зейделя скорее всего не сойдётся на системе уравнений, составленной прямым применением законов Кирхгофа.
В связи с описанной выше проблемой система уравнений будет составляться методом контурных токов (хотя в определённых условиях метод Гаусса-Зейделя может не сойтись и для этой системы). Но прямое применение законов Кирхгофа всё равно необходимо, так как после применения метода контурных токов будут получены только контурные токи, но не сами токи схемы. По уравнениям, составленным по законам Кирхгофа, предполагается вычислять истинные значения токов схемы.
РУЧНОЙ МЕТОД РАСЧЁТА
Для расчёта обозначим на схеме элементы:
Приведённую выше схему можно упростить.
Резисторы R4 и R5 соединены последовательно, следовательно, их можно объединить в один. Объединённый резистор назовём R45. Его сопротивление будет равно R45=R4+R5.
Резисторы R7 и R10 соединены последовательно, следовательно, их можно объединить в один. Назовём его R710. Его сопротивление будет равно R710=R7+R10.
В результате преобразований получим следующую схему:
В схеме только резисторы и источники тока и напряжения. Решим схему методом контурных токов. Расставим направления токов, обозначим и обозначим направления контурных токов:
Непосредственно применим правила Кирхгофа. Это пригодится в дальнейшем для вычисления токов из контурных токов:
На рисунке изображено 6 узлов, но важны только 5. Шестой узел не даёт новой информации. Запишем уравнения по первому закону Кирхгофа для пяти узлов:
Теперь запишем уравнения по второму закону Кирхгофа. Чтобы не загромождать рисунок на нём не были обозначены направления напряжений. Направления напряжения будем считать совпадающим с направлением токов. Например, uR1 имеет направление от узла 1 к узлу 2, uR2 имеет направление от узла 2 к узлу 4.
Уравнения, записанные по второму закону Кирхгофа:
Заменим напряжения через токи по формуле u=i*R:
Следовательно, исходное задание сводится к решению системы уравнений:
Теперь заменим источник тока I1 на эквивалентный источник ЭДС E5. E5=(R2+R6*R9/(R6+R9))I1. Тогда получится следующая схема:
Составим уравнения для полученных контуров:
Теперь выразим токи через контурные токи.
Для ручного метода расчёта уравнения были записаны в матричной форме.
Законы теории электрических цепей в матричной форме с примерами моделирования с помощью MATLAB. Учебно-методическое пособие
| Информация о книге | |
| Автор | Фриск В. В., Ганин В. И., Степанова А. Г. |
| Формат | 60×88/16 |
Подробнее
Описание
Настоящая работа является учебно-методическим пособием по использованию матричных методов расчета и моделирования на MATLAB электрических процессов.
Кратко изложена теоретическая часть. Приведены подробно документированные примеры программ в версии MATLAB 2019а.
Данный материал рассчитан на студентов всех форм обучения, бакалавров, магистров и аспирантов университетов связи, инженерно-технических работников, также будет полезен учащимся техникумов и колледжей.
Материал соответствует ФГОС-3: 210700 – Инфокоммуникационные технологии и системы связи, 220700 – Автоматизация технологических процессов и производств, 30100 ‒ Информатика и вычислительная техника, 090900 – Информационная безопасность.
В продаже имеется вариант книги в цветном исполнении (с цветными рисунками). Цена книги 280 руб.
Характеристики
| Информация о книге | |
| Автор | Фриск В. В., Ганин В. И., Степанова А. Г. |
| Формат | 60×88/16 |
| Объем, стр | 44 стр. |
Настоящая работа является учебно-методическим пособием по использованию матричных методов расчета и моделирования на MATLAB электрических процессов.
Кратко изложена теоретическая часть. Приведены подробно документированные примеры программ в версии MATLAB 2019а.
Данный материал рассчитан на студентов всех форм обучения, бакалавров, магистров и аспирантов университетов связи, инженерно-технических работников, также будет полезен учащимся техникумов и колледжей.
Материал соответствует ФГОС-3: 210700 – Инфокоммуникационные технологии и системы связи, 220700 – Автоматизация технологических процессов и производств, 30100 ‒ Информатика и вычислительная техника, 090900 – Информационная безопасность.
В продаже имеется вариант книги в цветном исполнении (с цветными рисунками). Цена книги 280 руб.