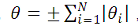значение погрешности без учета ее знака модуль погрешности это

Абсолютное значение погрешности

en absolute value of an error

fr valeur absolue d’une erreur

Значение погрешности без учета ее знака (мо­дуль погрешности)

Примечание — Необходимо различать термины абсолютная погрешность и абсолютное значение погрешности

9.11 относительная погрешность измерения;

de relativer Fehler (einer Messung)

fr erreur relative

Погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины.

Примечание — Относительную погрешность в долях или процентах находят из отношений

, или (9.4)

где — абсолютная погрешность измерений;

х—действительное или измеренное значение величины

9.12 рассеяние результатов в раду измерений;

Несовпадение результатов измерений одной и той же величины в ряду равноточных измере­ний, как правило, обусловленное действием слу­чайных погрешностей.

1 Количественную оценку рассеяния результатов в ряду измерений вследствие действия случайных погрешностей обычно получают после введения поправок на действие систематических погрешностей.

2 Оценками рассеяния результатов в ряду измерений могут быть:

средняя арифметическая погрешность (по модулю),

средняя квадратическая погрешность или стандартное отклонение (среднее квадратическое отклонение, экспериментальное среднее квадратическое отклонение),

доверительные границы погрешности (доверительная граница или доверительная погрешность)

9.13 размах результатов измерений;

Оценка Rn рассеяния результатов единичных измерений физической величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле

, (9.5) (9.5)

где х_max и х_min — наибольшее и наименьшее значения физической величины в данном ряду измерений.

Примечание — Рассеяние обычно обусловлено проявлением случайных причин при измерении и носит вероятностный характер

9.14 средняя квадратическая погрешность результатов единичных измерений в ряду измерений;

средняя квадратическая погрешность измерений;

средняя квадратическая погрешность;

en experimental standard deviation

fr écart-type experimental

Оценка S рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения, вычисляемая по формуле

(9.6)

где х_i,— результат i-го единичного измерения;`

x — среднее арифметическое значение измеряемой величины из и единичных результатов.

Примечание— На практике широко распрост­ранен термин среднее квадратическое отклонение — (СКО). Под отклонением в соответствии с формулой (9.6) понимают отклонение единичных результатов в ряду измерений от их среднего арифметического значения. В метрологии, как отмечено в 9.1, это отклонение называется погрешностью измерений. Если в результаты измерений введены поправки на действие систематических погрешностей, то отклонения представляют собой случайные погрешности. Поэтому с точки зрения упорядочения совокупности терминов, родовым среди которых является термин «погрешность измерения», целесообразно применять термин «средняя квадратическая погрешность». При обработке ряда результатов измерений, свободных от систематических погрешностей, СКП и СКО являются одинаковой оценкой рассеяния результатов единичных измерений

9.15 средняя квадратическая погрешность результата измерений среднего арифметического;

средняя квадратическая погрешность среднего арифметического;

средняя квадратическая погрешность; СКП

en experimental standard deviation of the mean

fr écart-type experimental de la moyenne Оценка S случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измере­ний, вычисляемая по формуле

(9.7)

где S— средняя квадратическая погрешность результатов единичных измерений, полученная из ряда равноточных измерений;

n— число единичных измерений в ряду

9.16 доверительные границы погрешности результата измерений;

доверительные границы погрешности;

Наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.

1 Доверительные границы в случае нормального закона распределения вычисляются как ±tS, ±tS где S, S средние квадратические погрешности, соответственно, единичного и среднего арифметического результатов измерений; t — коэффициент, зависящий от доверительной вероятности Р и числа измерений n.

2 При симметричных границах термин может применяться в единственном числе — доверительная граница.

3 Иногда вместо термина доверительная граница применяют термин доверительная погрешность или погрешность при данной доверительной вероятности

Поправка

Значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности.

Примечание — Знак поправки противоположен знаку погрешности. Поправку, прибавляемую к номинальному значению меры, называют поправкой к значению меры; поправку, вводимую в показание измерительного прибора, называют поправкой к показанию прибора

Поправочный множитель

en correction factor

fr coefficient de correction

Числовой коэффициент, на который умножают неисправленный результат измерения с целью исключения влияния систематической погрешности.

Примечание — Поправочный множитель используют в случаях, когда систематическая погрешность пропорциональна значению величины

9.19 точность результата измерений;

en accuracy of measurement

fr exactitude de mesure

Одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения.

Примечание — Считают, что чем меньше погрешность измерения, тем больше его точность

9.20 неопределенность измерений;

en uncertainty of measurement

fr incertitude de mesure

Параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине.

1 Определение взято из VIM—93 [1].

2 К определению в [1] приведены примечания, из которых следует, что:

а) параметром может быть стандартное отклонение или число, кратное ему) или половина интервала, имеющего указанный доверительный уровень;

б) неопределенность состоит (в основном) из многих составляющих. Некоторые из этих составляющих могут быть оценены экспериментальными стандартными отклонениями в статистически распределенной серии результатов измерений. Другие составляющие, которые также могут быть оценены стандартными отклонениями, базируются, на данных эксперимента или другой информации

Погрешность метода поверки

Погрешность применяемого метода передачи размера единицы при поверке

9.22 погрешность градуировки средства измерений;

Погрешность действительного значения вели­чины, приписанного той или иной отметке шкалы средства измерений в результате градуировки

9.23 погрешность воспроизведения единицы физи­ческой величины;

Погрешность результата измерений, выпол­няемых при воспроизведении единицы физической величины.

Примечание — Погрешность воспроизведения единицы при помощи государственных эталонов обычно ука­зывают в виде ее составляющих: неисключенной систематической погрешности; случайной погрешности; нестабильности за год

9.24 погрешность передачи размера единицы физи­ческой величины;

погрешность передачи размера единицы

Погрешность результата измерений, выпол­няемых при передаче размера единицы.

Примечание — В погрешность передачи размера единицы входят как неисключенные систематические, так и случайные погрешности метода и средств измерений

9.25 статическая погрешность измерений;

Погрешность результата измерений, свойствен­ная условиям статического измерения

9.26 динамическая погрешность измерений;

Погрешность результата измерений, свойствен­ная условиям динамического измерения

Промах

Погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.

Примечание — Иногда вместо термина «промах» применяют термин грубая погрешность измерений

9.28 предельная погрешность измерения в ряду измерений;

Максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи.

Примечание — Во многих случаях погрешность 3S принимают за предельную, то есть D_пр= ±3S. При необходимости за предельную погрешность может быть принято и другое значение погрешности (где S— см. термин 9.14).

9.29 погрешность результата однократного измерения;

Погрешность одного измерения (не входящего в ряд измерений), оцениваемая на основании известных погрешностей средства и метода измерений в данных условиях (измерений).

Пример — При однократном измерении микрометром какого-либо размера детали получено значение величины, равное 12,55 мм. При этом еще до измерении известно, что погрешность микрометра в данном диапазоне составляет ±0,01 мм, и погрешность метода (непосредственной оценки) в данном случае принята равной нулю. Следовательно,, погрешность полученного результата будет равна ±0,01 мм в данных условиях измерений

9.30 суммарная средняя квадратическая погрешность результата измерений;

суммарная погрешность результата; суммарная погрешность

Погрешность результата измерений (состоящая из суммы случайных и неисключенных систематических погрешностей, принимаемых за случайные), вычисляемая по формуле

(9.8)

где — средняя квадратическая погрешности суммы неисключенных систематических погрешностей при равномерном распределении (принимаемых за случайные).

Примечание — Доверительные границы суммарной погрешности (Dx)å могут быть вычислены по формуле

(9.9)

где ; — граница суммы неисключенных систематических погрешностей результата измерений, вычисляемая по формулам (9.2) или (9.3); t·S — доверитель­ная граница погрешности результата измерений по 9.16

Источник

главная

измерения

метрологическая экспертиза

форум

полезная информация

Метрология термины и определения

7 Принципы, методы и методики измерений

8 Результаты измерений физических величин

9 Погрешности измерений

10 Погрешности средств измерений

11 Условия измерений

12 Эталоны единиц физических величин

13 Метрологическая служба и ее деятельность

9 Погрешности измерений

9.1 погрешность результата измерения;

Отклонение результата измерения от истинного (действительного) значения измеряемой величины.

Синонимом термина погрешность измерения является термин ошибка измерения, применять который не рекомендуется как менее удачный

Составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины.

Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей

Составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений

9.4 погрешность метода измерений;

Составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений.

1 Вследствие упрощений, принятых в уравнениях для измерений, нередко возникают существенные погрешности, для компенсации действия которых следует вводить поправки. Погрешность метода иногда называют теоретической погрешностью.

2 Иногда погрешность метода может проявляться как случайная

Составляющая систематической погрешности измерения, являющаяся следствием неучтенного влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения.

Составляющая систематической погрешности измерений, обусловленная индивидуальными особенностями оператора.

1 Встречаются операторы, которые систематически опаздывают (или опережают) снимать отсчеты показаний средств измерений

2 Иногда субъективную погрешность называют личной погрешностью или личной разностью

Составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости.

Составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины

Погрешность измерения, выраженная в единицах измеряемой величины

Значение погрешности без учета ее знака (модуль погрешности)

Погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины.

Несовпадение результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обусловленное действием случайных погрешностей.

1 Количественную оценку рассеяния результатов в ряду измерений вследствие действия случайных погрешностей обычно получают после введения поправок на действие систематических погрешностей.

2 Оценками рассеяния результатов в ряду измерений могут быть:

средняя арифметическая погрешность (по модулю),

средняя квадратическая погрешность или стандартное отклонение (среднее квадратическое отклонение, экспериментальное среднее квадратическое отклонение),

доверительные границы погрешности (доверительная граница или доверительная погрешность)

Оценка R_n рассеяния результатов единичных измерений физической величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле

средняя квадратическая погрешность измерений;

средняя квадратическая погрешность;

Оценка рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения

9.15 средняя квадратическая погрешность результата измерений среднего арифметического ;

средняя квадратическая погрешность среднего арифметического;

средняя квадратическая погрешность ;

Оценка S x случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений, вычисляемая по формуле

доверительные границы погрешности;

Наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.

3 Иногда вместо термина доверительная граница применяют термин доверительная погрешность или погрешность при данной доверительной вероятности

Значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности.

Числовой коэффициент, на который умножают неисправленный результат измерения с целью исключения влияния систематической погрешности.

Одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения.

Параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине.

1 Определение взято из VIM-93 [1].

2 К определению в [1] приведены примечания, из которых следует, что:

а) параметром может быть стандартное отклонение (или число, кратное ему) или половина интервала, имеющего указанный доверительный уровень;

б) неопределенность состоит (в основном) из многих составляющих. Некоторые из этих составляющих могут быть оценены экспериментальными стандартными отклонениями в статистически распределенной серии результатов измерений. Другие составляющие, которые также могут быть оценены стандартными отклонениями, базируются на данных эксперимента или другой информации

Погрешность применяемого метода передачи размера единицы при поверке

Погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки

Погрешность результата измерений, выполняемых при воспроизведении единицы физической величины.

погрешность передачи размера единицы

Погрешность результата измерений, выполняемых при передаче размера единицы.

Погрешность результата измерений, свойственная условиям статического измерения

Погрешность результата измерений, свойственная условиям динамического измерения

Погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.

Максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи.

Погрешность одного измерения (не входящего в ряд измерений), оцениваемая на основании известных погрешностей средства и метода измерений в данных условиях (измерений).

суммарная погрешность результата;

Погрешность результата измерений (состоящая из суммы случайных и неисключенных систематических погрешностей, принимаемых за случайные), вычисляемая по формуле

где

— средняя квадратическая погрешность суммы неисключенных систематических погрешностей при равномерном распределении (принимаемых за случайные).

Источник

Значение погрешности без учета ее знака модуль погрешности это

Всероссийский научно-исследовательский институт
оптико-физических измерений

ПОИСК И НАВИГАЦИЯ

МЫ НА YOUTUBE

Погрешности измерений

Погрешность результата измерения (англ. error of a measurement) – отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Примечания:

Инструментальная погрешность измерения (англ. instrumental error) – составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений.

Погрешность метода измерений (англ. error of method) – составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений.
Примечания:

Погрешность (измерения) из-за изменений условий измерения – составляющая систематической погрешности измерения, являющаяся следствием неучтенного влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения.
Примечание. Этот термин применяют в случае неучтенного или недостаточно учтенного действия той или иной влияющей величины (температуры, атмосферного давления, влажности воздуха, напряженности магнитного поля, вибрации и др.); неправильной установки средств измерений, нарушения правил их взаимного расположения и др.

Субъективная погрешность измерения – составляющая систематической погрешности измерений, обусловленная индивидуальными особенностями оператора.
Примечания:

Неисключенная систематическая погрешность – составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости.
Примечания:

Случайная погрешность измерения (англ. random error) – составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины.

Абсолютная погрешность измерения (англ. absolute error of a measurement) – погрешность измерения, выраженная в единицах измеряемой величины.

Абсолютное значение погрешности (англ. absolute value of an error) – значение погрешности без учета ее знака (модуль погрешности).
Примечание. Необходимо различать термины абсолютная погрешность и абсолютное значение погрешности.

Относительная погрешность измерения (англ. relative error) – погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины.
Примечание. Относительную погрешность в долях или процентах находят из отношений:

Рассеяние результатов в ряду измерений (англ. dispersion) – несовпадение результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обусловленное действием случайных погрешностей.
Примечания:

Размах результатов измерений (англ. ) – оценка R_n рассеяния результатов единичных измерений физической n величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле:

Среднее квадратическое отклонение результатов единичных измерений в ряду измерений (англ. experimental (sample) standard deviation) – характеристика S рассеяния результатов измерений в ряду равноточных измерений одной и той же физической величины, вычисляемая по формуле:

Среднее квадратическое отклонение среднего арифметического значения результатов измерений (англ. experimental (sample) standard deviation) – характеристика S_x рассеяния среднего арифметического значения результатов равноточных измерений одной и той же величины, вычисляемая по формуле:

Доверительные границы погрешности результата измерений – наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.

Поправка (англ. correction) – значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности.
Примечание. Знак поправки противоположен знаку погрешности. Поправку, прибавляемую к номинальному значению меры, называют поправкой к значению меры; поправку, вводимую в показание измерительного прибора, называют поправкой к показанию прибора.

Поправочный множитель (англ. correction factor) – числовой коэффициент, на который умножают неисправленный результат измерения с целью исключения влияния систематической погрешности.
Примечание. Поправочный множитель используют в случаях, когда систематическая погрешность пропорциональна значению величины.

Точность результата измерений (англ. accuracy of measurement) – одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения.
Примечание. Считают, что чем меньше погрешность измерения, тем больше его точность.

Неопределенность измерений (англ. uncertainty of measurement) – параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине.

Погрешность метода поверки – погрешность применяемого метода передачи размера единицы при поверке.

Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.

Погрешность воспроизведения единицы физической величины – погрешность результата измерений, выполняемых при воспроизведении единицы физической величины.
Примечание. Погрешность воспроизведения единицы при помощи государственных эталонов обычно указывают в виде ее составляющих: неисключенной систематической погрешности; случайной погрешности; нестабильности за год.

Погрешность передачи размера единицы физической величины – погрешность результата измерений, выполняемых при передаче размера единицы.
Примечание. В погрешность передачи размера единицы входят как неисключенные систематические, так и случайные погрешности метода и средств измерений.

Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения.

Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения.

Промах – погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.
Примечание. Иногда вместо термина промах применяют термин грубая погрешность измерений.

Предельная погрешность измерения в ряду измерений – максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи.

Погрешность результата однократного измерения – погрешность одного измерения (не входящего в ряд измерений), оцениваемая на основании известных погрешностей средства и метода измерений в данных условиях (измерений).
Пример. При однократном измерении микрометром какого-либо размера детали получено значение величины, равное 12,55 мм. При этом еще до измерения известно, что погрешность микрометра в данном диапазоне составляет +/- 0,01 мм, и погрешность метода (непосредственной оценки) в данном случае принята равной нулю. Следовательно, погрешность полученного результата будет равна +/- 0,01 мм в данных условиях измерений.

Суммарное среднее квадратическое отклонение среднего арифметического значения результатов измерений – характеристика S_∑ рассеяния среднего арифметического результатов измерений, обусловленная влиянием случайных и неисключенных систематических погрешностей и вычисляемая по формуле:

Источник

• ← значение плана счетов бухгалтерского учета
• значение показателя результативности использования субсидии →