есть сосуды разной геометрической формы в них налита одна и та же жидкость
Равновесие, закон Паскаля, сила Архимеда, математический и пружинный маятники, механические волны, звук
Теория к заданию 4 из ЕГЭ по физике
Равновесие механической системы (абсолютно твердого тела)
Равновесие механической системы — это состояние, при котором все точки механической системы находятся в покое по отношению к рассматриваемой системе отсчета. Если система отсчета инерциальна, равновесие называется абсолютным, если неинерциальна — относительным.
Для нахождения условий равновесия абсолютно твердого тела необходимо мысленно разбить его на большое число достаточно малых элементов, каждый из которых можно представить материальной точкой. Все эти элементы взаимодействуют между собой — эти силы взаимодействия называются внутренними. Помимо этого на ряд точек тела могут действовать внешние силы.
Согласно второму закону Ньютона, чтобы ускорение точки равнялось нулю (а ускорение покоящейся точки равно нулю), геометрическая сумма сил, действующих на эту точку, должна быть равна нулю. Если тело находится в покое, значит, все его точки (элементы) также находятся в покое. Следовательно, для любой точки тела можно записать:
Уравнение означает, что для равновесия тела необходимо и достаточно, чтобы геометрическая сумма всех сил, действующих на любой элемент этого тела, была равна нулю.
Из уравнения легко получить первое условие равновесия тела (системы тел). Для этого достаточно просуммировать уравнение по всем элементам тела:
Вторая сумма равна нулю согласно третьему закону Ньютона: векторная сумма всех внутренних сил системы равна нулю, т. к. любой внутренней силе соответствует сила, равная по модулю и противоположная по направлению.
Первым условием равновесия твердого тела (системы тел) является равенство нулю геометрической суммы всех внешних сил, приложенных к телу.
Это условие является необходимым, но не достаточным. В этом легко убедиться, вспомнив о вращающем действии пары сил, геометрическая сумма которых тоже равна нулю.
Вторым условием равновесия твердого тела является равенство нулю суммы моментов всех внешних сил, действующих на тело, относительно любой оси.
Таким образом, условия равновесия твердого тела в случае произвольного числа внешних сил выглядят так:
Закон Паскаля
Гидростатика (от греч. hydor — вода и statos — стоящий) — один из подразделов механики, изучающий равновесие жидкости, а также равновесие твердых тел, частично или полностью погруженных в жидкость.
Закон Паскаля — основной закон гидростатики, согласно которому давление на поверхность жидкости, произведенное внешними силами, передается жидкостью одинаково во всех направлениях.
Этот закон был открыт французским ученым Б. Паскалем в 1653 г. и опубликован в 1663 г.
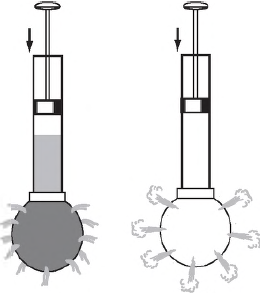
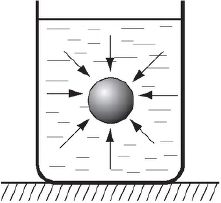
Чтобы убедиться в справедливости закона Паскаля, достаточно проделать простой опыт. Присоединим к трубке с поршнем полый шар со множеством маленьких отверстий. Наполнив шар водой, нажмем на поршень, чтобы увеличить в нем давление. Вода начнет выливаться, но не только через то отверстие, которое находится на линии действия прилагаемой нами силы, а и через все остальные тоже. Причем напор воды, обусловленный внешним давлением, во всех появившихся струйках будет одинаковым.
Аналогичный результат мы получим в том случае, если вместо воды будем использовать дым. Таким образом, закон Паскаля справедлив не только для жидкостей, но и для газов.
Жидкости и газы передают оказываемое на них давление по всем направлениям одинаково.
Передача давления жидкостями и газами во всех направлениях одновременно объясняется достаточно высокой подвижностью частиц, из которых они состоят.
Давление покоящейся жидкости на дно и стенки сосуда (гидростатическое давление)
Жидкости (и газы) передают по всем направлениям не только внешнее давление, но и то давление, которое существует внутри них благодаря весу собственных частей.
Давление, оказываемое покоящейся жидкостью, называется гидростатическим.
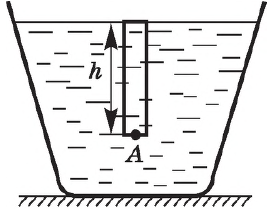
Сила давления, действующая со стороны вышележащего узкого столба жидкости, может быть выражена двумя способами:
а объем — через высоту столба и площадь его поперечного сечения:
Это и есть формула гидростатического давления.
Гидростатическое давление на любой глубине внутри жидкости не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободного падения и глубины, на которой определяется давление.
Важно еще раз подчеркнуть, что по формуле гидростатического давления можно рассчитывать давление жидкости, налитой в сосуд любой формы, в том числе давление на стенки сосуда, а также давление в любой точке жидкости, направленное снизу вверх, поскольку давление на одной и той же глубине одинаково по всем направлениям.
Гидростатический парадокс
Гидростатический парадокс — явление, заключающееся в том, что вес жидкости, налитой в сосуд, может отличаться от силы давления жидкости на дно сосуда.
В данном случае под словом «парадокс» понимают неожиданное явление, не соответствующее обычным представлениям.
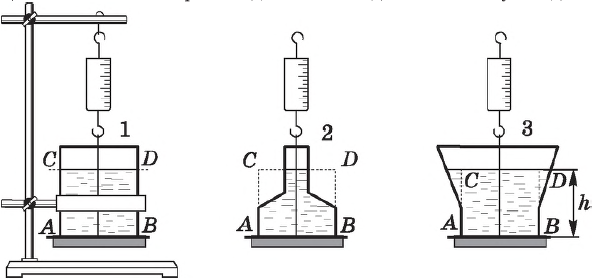
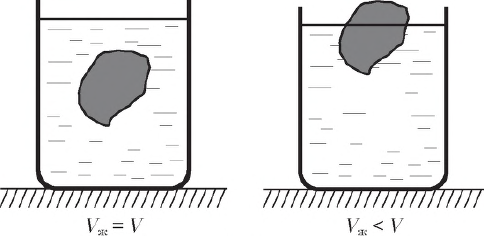
Так, в расширяющихся кверху сосудах сила давления на дно меньше веса жидкости, а в сужающихся — больше. В цилиндрическом сосуде обе силы одинаковы. Если одна и та же жидкость налита до одной и той же высоты в сосуды разной формы, но с одинаковой площадью дна, то, несмотря на разный вес налитой жидкости, сила давления на дно одинакова для всех сосудов и равна весу жидкости в цилиндрическом сосуде.
Гидростатический парадокс объясняется законом Паскаля — способностью жидкости передавать давление одинаково во всех направлениях.
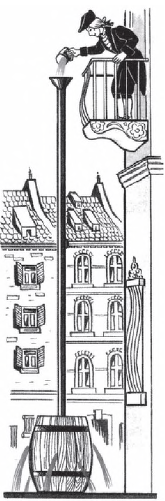
Из формулы гидростатического давления следует, что одно и то же количество воды, находясь в разных сосудах, может оказывать разное давление на дно. Поскольку это давление зависит от высоты столба жидкости, то в узких сосудах оно будет больше, чем в широких. Благодаря этому даже небольшим количеством воды можно создавать очень большое давление. В 1648 г. это очень убедительно продемонстрировал Б. Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, вылил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.
Закон Архимеда
Закон Архимеда — закон статики жидкостей и газов, согласно которому на всякое тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная весу вытесненной телом жидкости (газа) и направленная по вертикали вверх.
Этот закон был открыт древнегреческим ученым Архимедом в III в. до н. э. Свои исследования Архимед описал в трактате «О плавающих телах», который считается одним из последних его научных трудов.
Ниже приведены выводы, следующие из закона Архимеда.
Действие жидкости и газа на погруженное в них тело
Если погрузить в воду мячик, наполненный воздухом, и отпустить его, то он всплывет. То же самое произойдет со щепкой, с пробкой и многими другими телами. Какая же сила заставляет их всплывать?
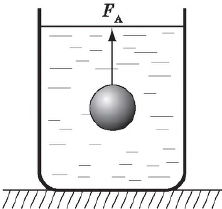
На тело, погруженное в воду, со всех сторон действуют силы давления воды. В каждой точке тела эти силы направлены перпендикулярно его поверхности. Если бы все эти силы были одинаковы, тело испытывало бы лишь всестороннее сжатие. Но на разных глубинах гидростатическое давление различно: оно возрастает с увеличением глубины. Поэтому силы давления, приложенные к нижним участкам тела, оказываются больше сил давления, действующих на тело сверху.
Архимедова (выталкивающая) сила действует на тело не только в воде, но и в любой другой жидкости, т. к. в любой жидкости существует гидростатическое давление, разное на разных глубинах. Эта сила действует и в газах, благодаря чему летают воздушные шары и дирижабли.
Благодаря выталкивающей силе вес любого тела, находящегося в воде (или в любой другой жидкости), оказывается меньше, чем в воздухе, а в воздухе меньше, чем в безвоздушном пространстве. В этом легко убедиться, взвесив гирю с помощью учебного пружинного динамометра сначала в воздухе, а затем опустив ее в сосуд с водой.
Уменьшение веса происходит и при переносе тела из вакуума в воздух (или какой-либо другой газ).
Поэтому чтобы найти архимедову силу, действующую на тело в какой-либо жидкости, нужно это тело взвесить в воздухе и в жидкости. Разность полученных значений и будет архимедовой (выталкивающей) силой.
Выталкивающая сила, действующая на погруженное в жидкость тело, равна весу жидкости, вытесненной этим телом.
С учетом вышеизложенного закон Архимеда можно сформулировать так:
На всякое тело, погруженное в покоящуюся жидкость (или газ), действует со стороны этой жидкости (или газа) выталкивающая сила, равная произведению плотности жидкости (или газа), ускорения свободного падения и объема той части тела, которая погружена в жидкость (или газ).
Свободные колебания математического и пружинного маятников
Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинетической) при отсутствии внешних воздействий.
Потенциальная или кинетическая энергия может быть сообщена, например, в механических системах через начальное смещение или начальную скорость.
Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними образуют систему тел, которая называется колебательной системой.
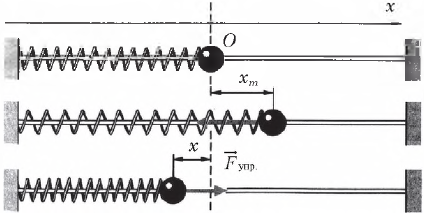
Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний конец пружины, входят в колебательную систему. Здесь шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.
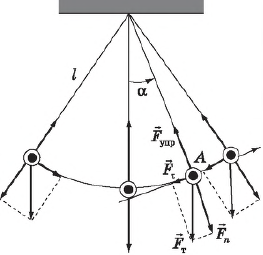
Другим классическим примером механической колебательной системы является математический маятник. В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити (в колебательную систему входит также Земля). Их равнодействующая направлена к положению равновесия. Силы, действующие между телами колебательной системы, называются внутренними силами. Внешними силами называются силы, действующие на систему со стороны тел, не входящих в нее. С этой точки зрения свободные колебания можно определить как колебания в системе под действием внутренних сил после того, как система выведена из положения равновесия.
Условиями возникновения свободных колебаний являются:
Динамика свободных колебаний
Это дифференциальное уравнение движения тела, колеблющегося под действием силы упругости: вторая производная координаты по времени <ускорение тела) прямо пропорциональна его координате, взятой с противоположным знаком.
Таким образом, свободные колебания описываются уравнениями одного вида (подчиняются одним и тем же законам) независимо от физической природы сил, вызывающих эти колебания.
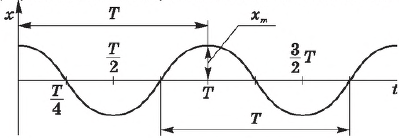
То есть координата тела, совершающего свободные колебания, меняется с течением времени по закону косинуса или синуса, и, следовательно, эти колебания являются гармоническими.
Циклическая частота и период свободных гармонических колебаний определяются свойствами системы. Так, для колебаний тела, прикрепленного к пружине, справедливы соотношения:
Собственная частота тем больше, чем больше жесткость пружины или меньше масса груза, что вполне подтверждается опытом.
Для математического маятника выполняются равенства:
Эта формула была впервые получена и проверена на опыте голландским ученым Гюйгенсом (современником Ньютона).
Период колебаний возрастает с увеличением длины маятника и не зависит от его массы.
Следует особо обратить внимание на то, что гармонические колебания являются строго периодическими (т. к. подчиняются закону синуса или косинуса) и даже для математического маятника, являющегося идеализацией реального (физического) маятника, возможны только при малых углах колебания. Если углы отклонения велики, смещение груза не будет пропорционально углу отклонения (синусу угла) и ускорение не будет пропорционально смещению.
Фаза колебаний
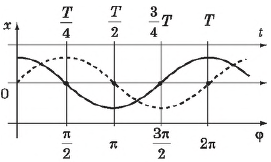
Фаза колебаний — это аргумент периодически изменяющейся функции, описывающей колебательный или волновой процесс.
Для гармонических колебаний
Затухающие колебания
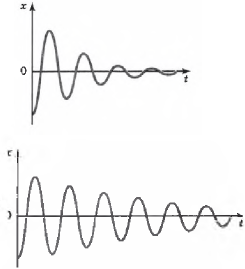
Затухание колебаний — это уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Свободные колебания всегда являются затухающими колебаниями.
Потери энергии колебаний в механических системах связаны с превращением ее в теплоту вследствие трения и сопротивления окружающей среды.
Так, механическая энергия колебаний маятника расходуется на преодоление сил трения и сопротивления воздуха, переходя при этом во внутреннюю энергию.
Амплитуда колебаний постепенно уменьшается, и через некоторое время колебания прекращаются. Такие колебания называются затухающими.
Чем больше силы сопротивления движению, тем быстрее прекращаются колебания. Например, в воде колебания прекращаются быстрее, чем в воздухе.
Упругие волны (механические волны)
Возмущения, распространяющиеся в пространстве, удаляясь от места их возникновения, называют волнами.
Упругие волны — это возмущения, распространяющиеся в твердой, жидкой и газообразной средах благодаря действию в них сил упругости.
Сами эти среды называют упругими. Возмущение упругой среды — это любое отклонение частиц этой среды от своего положения равновесия.
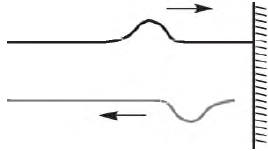
Возьмем, например, длинную веревку (или резиновую трубку) и прикрепим один из ее концов к стене. Туго натянув веревку, резким боковым движением руки создадим на ее незакрепленном конце кратковременное возмущение. Мы увидим, что это возмущение побежит вдоль веревки и, дойдя до стены, отразится назад.
Начальное возмущение среды, приводящее к появлению в ней волны, вызывается действием в ней какого-нибудь инородного тела, которое называют источником волны. Это может быть рука человека, ударившего по веревке, камешек, упавший в воду, и т. д.
Если действие источника носит кратковременный характер, то в среде возникает так называемая одиночная волна. Если же источник волны совершает длительное колебательное движение, то волны в среде начинают идти одна за другой. Подобную картину можно увидеть, поместив над ванной с водой вибрирующую пластину, имеющую наконечник, опущенный в воду.
Необходимым условием возникновения упругой волны является появление в момент возникновения возмущения сил упругости, препятствующих этому возмущению. Эти силы стремятся сблизить соседние частицы среды, если они расходятся, и отдалить их, когда они сближаются. Действуя на все более удаленные от источника частицы среды, силы упругости начинают выводить их из положения равновесия. Постепенно все частицы среды одна за другой вовлекаются в колебательное движение. Распространение этих колебаний и проявляется в виде волны.
В любой упругой среде одновременно существуют два вида движения: колебания частиц среды и распространение возмущения. Волна, в которой частицы среды колеблются вдоль направления ее распространения, называется продольной, а волна, в которой частицы среды колеблются поперек направления ее распространения, называется поперечной.
Продольная волна
Волна, в которой колебания происходят вдоль направления распространения волны, называется продольной.
В упругой продольной волне возмущения представляют собой сжатия и разрежения среды. Деформация сжатия сопровождается возникновением сил упругости в любой среде. Поэтому продольные волны могут распространяться во всех средах (и в жидких, и в твердых, и в газообразных).
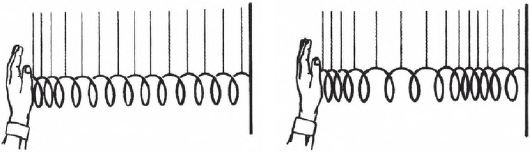
Пример распространения продольной упругой волны изображен на рисунке. По левому концу длинной пружины, подвешенной на нитях, ударяют рукой. От удара несколько витков сближаются, возникает сила упругости, под действием которой эти витки начинают расходиться. Продолжая движение по инерции, они будут продолжать расходиться, минуя положение равновесия и образуя в этом месте разрежение. При ритмичном воздействии витки на конце пружины будут то сближаться, то отходить друг от друга, т. е. колебаться возле своего положения равновесия. Эти колебания постепенно передадутся от витка к витку вдоль всей пружины. По пружине распространятся сгущения и разрежения витков, или упругая волна.
Поперечная волна
Волны, в которых колебания происходят перпендикулярно направлению их распространения, называются поперечными.
В поперечной упругой волне возмущения представляют собой смещения (сдвиги) одних слоев среды относительно других. Деформация сдвига приводит к появлению сил упругости только в твердых телах: сдвиг слоев в газах и жидкостях возникновением сил упругости не сопровождается. Поэтому поперечные волны могут распространяться только в твердых телах.
Плоская волна
Плоская волна — это волна, у которой направление распространения одинаково во всех точках пространства.
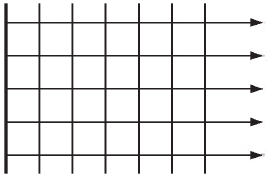
В такой волне амплитуда не меняется со временем (по мере удаления от источника). Получить такую волну можно, если большую пластину, находящуюся в сплошной однородной упругой среде, заставить колебаться перпендикулярно плоскости. Тогда все точки среды, примыкающей к пластине, будут колебаться с одинаковыми амплитудами и одинаковыми фазами. Распространяться эти колебания будут в виде волн в направлении нормали к пластине, причем все частицы среды, лежащие в плоскостях, параллельных пластине, будут колебаться с одинаковыми фазами.
Геометрическое место точек, в которых фаза колебаний имеет одно и то же значение, называется волновой поверхностью, или фронтом волны.
С этой точки зрения плоской волне можно дать и следующее определение.
Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу.
Линия, нормальная к волновой поверхности, называется лучом. Вдоль лучей происходит перенос энергии волны. Для плоских волн лучи — это параллельные прямые.
Уравнение плоской синусоидальной волны имеет вид:
Сферическая волна
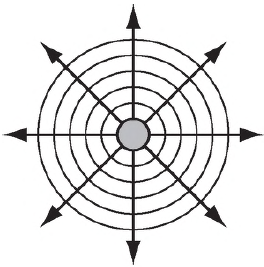
Сферической называется волна, волновые поверхности которой имеют вид концентрических сфер. Центр этих сфер называется центром волны.
Лучи в такой волне направлены вдоль радиусов, расходящихся от центра волны. На рисунке источником волны является пульсирующая сфера.
Амплитуда колебаний частиц в сферической волне обязательно убывает по мере удаления от источника. Энергия, излучаемая источником, равномерно распределяется по поверхности сферы, радиус которой непрерывно увеличивается по мере распространения волны. Уравнение сферической волны имеет вид:
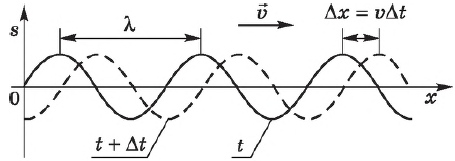
Длина и скорость волны
Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника, т. к. колебания частиц в среде являются вынужденными и не зависят от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Интерференция и дифракция волн
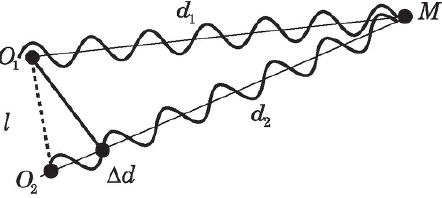
Интерференция волн (от лат. inter — взаимно, между собой и ferio — ударяю, поражаю) — взаимное усиление или ослабление двух (или большего числа) волн при их наложении друг на друга при одновременном распространении в пространстве.
Обычно под интерференционным эффектом понимают тот факт, что результирующая интенсивность в одних точках пространства получается больше, в других — меньше суммарной интенсивности волн.
Интерференция волн — одно из основных свойств волн любой природы: упругих, электромагнитных, в том числе и световых, и др.
Интерференция механических волн
Сложение механических волн — их взаимное наложение — проще всего наблюдать на поверхности воды. Если возбудить две волны, бросив в воду два камня, то каждая из этих волн ведет себя так, как будто другой волны не существует. Аналогично ведут себя звуковые волны от разных независимых источников. В каждой точке среды колебания, вызванные волнами, просто складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.
Слово «эхо» связано с именем горной нимфы Эхо, которая, согласно древнегреческой мифологии, безответно была влюблена в Нарцисса. От тоски по возлюбленному Эхо высохла и окаменела так, что от нее остался лишь голос, способный повторять окончания произнесенных в ее присутствии слов.
А это значительно меньше времени ($0.06$ с), необходимого, чтобы услышать эхо.
Увеличение длительности звука, вызванное его отражениями от различных препятствий, называется реверберацией. Реверберация велика в пустых помещениях, где она приводит к гулкости. И наоборот, помещения с мягкой обивкой стен, драпировками, шторами, мягкой мебелью, коврами, а также наполненные людьми хорошо поглощают звук, и потому реверберация в них незначительна.
Скорость звука
Для распространения звука необходима упругая среда. В вакууме звуковые волны распространяться не могут, так как там нечему колебаться. В этом можно убедиться на простом опыте. Если поместить под стеклянный колокол электрический звонок, то по мере выкачивания из-под колокола воздуха звук от звонка будет становиться все слабее и слабее, пока не прекратится совсем.
Известно, что во время грозы мы видим вспышку молнии и лишь через некоторое время слышим раскаты грома. Это запаздывание возникает из-за того, что скорость звука в воздухе значительно меньше скорости света, идущего от молнии.
Скорость звука в твердых телах больше, чем в жидкостях и газах. Если приложить ухо к рельсу, то после удара по другому концу рельса слышно два звука. Один из них достигает уха по рельсу, другой — по воздуху.
Хорошей проводимостью звука обладает земля. Поэтому в старые времена при осаде в крепостных стенах помещали «слухачей», которые по звуку, передаваемому землей, могли определить, ведет ли враг подкоп к стенам или нет. Прикладывая ухо к земле, также следили за приближением вражеской конницы.
Твердые тела хорошо проводят звук. Благодаря этому люди, потерявшие слух, иной раз способны танцевать под музыку, которая доходит до слуховых нервов не через воздух и наружное ухо, а через пол и кости.
Скорость звука можно определить, зная длину волны и частоту (или период) колебаний:
Инфразвук
Рассказывают, что однажды американский физик Р. Вуд (прослывший среди коллег большим оригиналом и весельчаком) принес в театр специальный аппарат, излучающий инфразвуковые волны, и, включив его, направил на сцену. Никакого звука никто не услышал, однако с актрисой случилась истерика.
Резонансным влиянием на человеческий организм низкочастотных звуков объясняется и возбуждающее действие современной рок-музыки, насыщенной многократно усиленными низкими частотами барабанов, бас-гитар.
Источниками инфразвука могут служить грозовые разряды, выстрелы, извержения вулканов, работающие двигатели реактивных самолетов, ветер, обтекающий гребни морских волн, и т. д. Для инфразвука характерно малое поглощение в различных средах, вследствие чего он может распространяться на очень большие расстояния. Это позволяет определить места сильных взрывов, положение стреляющего орудия, осуществлять контроль за подземными ядерными взрывами, предсказывать цунами и т. д.
Ультразвук
Ультразвуковые сигналы используются и некоторыми китами. Эти сигналы позволяют им охотиться на кальмаров при полном отсутствии света.
Использование ультразвука в технике. Ультразвук находит широкое применение в науке и технике, где его получают с помощью различных механических (например, сирена) и электромеханических устройств.
Источники ультразвука устанавливают на кораблях и подводных лодках. Посылая короткие импульсы ультразвуковых волн, можно уловить их отражения от дна или каких-либо других предметов. По времени запаздывания отраженной волны можно судить о расстоянии до препятствия. Использующиеся при этом эхолоты и гидролокаторы позволяют измерять глубину моря, решать различные навигационные задачи (плавание вблизи скал, рифов и т. д.), осуществлять рыбопромысловую разведку (обнаруживать косяки рыб), а также решать военные задачи (поиск подводных лодок противника, бесперископные торпедные атаки и др.).
В промышленности по отражению ультразвука от трещин в металлических отливках судят о дефектах в изделиях.
Ультразвуки дробят жидкие и твердые вещества, образуя различные эмульсии и суспензии.
Преобразование ультразвука в электрические колебания, а их затем в свет позволяет осуществить звуковидение. При помощи звуковидения можно видеть предметы в непрозрачной для света воде.
В медицине при помощи ультразвука осуществляют сварку сломанных костей, обнаруживают опухоли, осуществляют диагностические исследования в акушерстве и т. д. Биологическое действие ультразвука (приводящее к гибели микробов) позволяет использовать его для пастерилизации молока, стерилизации медицинских инструментов.