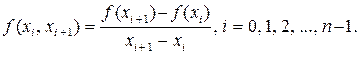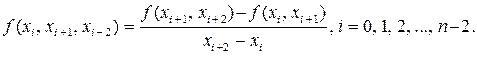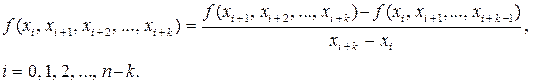интерполяционный полином в форме ньютона
Интерполяционный многочлен Ньютона (полином Ньютона)
Этот онлайн калькулятор строит интерполяционный многочлен Ньютона для заданного набора точек. Калькулятор показывает пошаговое решение, интерполирует заданные точки, а также строит график.
Калькулятор ниже строит интерполяционный многочлен Ньютона (полином Ньютона) в общем виде (то есть ему не требуется, чтобы точки из набора значений находились друг от друга на равном расстоянии), после чего упрощает его, раскрывая скобки, и получает результат, пригодный для расчетов. Помимо этого калькулятор интерполирует значения неизвестной функции в указанных точках и строит график полинома, отмечая точки интерполяции и точки из заданного набора данных.
Как пользоваться
Теория и формулы, как обычно, описаны под калькулятором.
Интерполяционный многочлен Ньютона (полином Ньютона)
Интерполяционный многочлен Ньютона (полином Ньютона)
В общем виде интерполяционный многочлен Ньютона записывается в следующем виде:
Разделенную разность k-го порядка также можно выразить через значения функции в точках с помощью такой формулы:
.
Последняя формула и используется в калькуляторе.
При этом сам интерполяционный полином для заданного набора данных является единственным, и по сути, полином Ньютона только по форме отличается от полинома Лагранжа, после упрощения превращаясь в один и тот же полином.
Интерполяционный многочлен в форме Ньютона
Интерполяционный многочлен в форме Ньютона
1. Интерполяционная формула Ньютона для неравноотстоящих значений аргумента
В общем виде интерполяционный многочлен в форме Ньютона записывается в следующем виде:
где n – вещественное число, которое указывает степень полинома;

Разделённая разность является симметричной функцией своих аргументов, то есть при любой их перестановке её значение не меняется. Следует отметить, что для разделённой разности k-го порядка справедлива следующая формула:
В качестве примера, рассмотрим построение полинома в форме Ньютона по представленной выборке данных, которая состоит из трех заданных точек 
• Разделенная разность 1-го порядка определяется следующим выражением
Следует отметить, что данное выражение может быть переписано в другом виде:
• Разделенная разность 2-го порядка определяется следующим выражением
Следует отметить, что данное выражение может быть переписано в другом виде:
Форма Ньютона является удобной формой представления интерполяционного полинома n-степени, так как при добавлении дополнительного узла все вычисленные ранее слагаемые остаются без изменения, а к выражению добавляется только одно новое слагаемое. Следует отметить, что интерполяционный полином в форме Ньютона только по форме отличается от интерполяционного полинома в форме Лагранжа, представляя собой на заданной сетке один и тот же интерполяционный полином.
Следует отметить, что полином в форме Ньютона может быть представлен в более компактном виде (по схеме Горнера), которая получается путем последовательного вынесения за скобки множителей
2. Интерполяционная формула Ньютона для равноотстоящих значений аргумента
В случае если значения функции заданы для равноотстоящих значений аргумента, которые имеют постоянный шаг измерений 
• Для интерполирования функции в конце рассматриваемого интервала (интерполирование назад и экстраполирование вперед) используют интерполяционный полином в форме Ньютона в следующей записи:
Получаемые конечные разности удобно представлять в табличной форме записи, в виде горизонтальной таблице конечных разностей. В этой формуле из таблицы конечных разностей используются 
• Для интерполирования функции в начале рассматриваемого интервала (интерполирование вперед и экстраполирование назад) используют интерполяционный полином в форме Ньютона в следующей записи:
Получаемые конечные разности удобно представлять в табличной форме записи, в виде горизонтальной таблице конечных разностей. В формуле из таблицы конечных разностей используются 
3. Погрешность интерполяционного полинома в форме Ньютона
Рассмотрим функцию f ( x ), которая непрерывна и дифференцируема на рассматриваемом отрезке [a, b]. Интерполяционный полином P (x) в форме Ньютона принимает в точках 

Абсолютную погрешность интерполяционной формулы Ньютона определяют следующим образом:
Переменная 
В случае равноотстоящих узлов 
Выражение записано с учетом следующей формулы:
Выбор узлов интерполяции
С помощью корректного выбора узлов можно минимизировать значение 
В качестве узлов следует взять корни этого многочлена, то есть точки:
4. Методика вычисления полинома в форме Ньютона (прямой способ)
Алгоритм вычисления полинома в форме Ньютона позволяет разделить задачи определения коэффициентов и вычисления значений полинома при различных значениях аргумента:
2. Выполняется вычисление разделенных разностей n-порядка, которые будет использоваться для построения полинома в форме Ньютона.
3. Выполняется вычисление полинома n-степени в форме Ньютона по следующей формуле:
Алгоритм вычисления полинома в форме Ньютона 
Следует отметить, что разделённые разности k-го порядка в соответствии с представленной методикой перезаписывается в вектор столбец функции 


В качестве примера рассмотрим следующую практическую задачу. В рамках задачи известен набор шести значений, которые получены методом случайной выборки для различных моментов времени. Следует отметить, что данная выборка значений описывает функция 

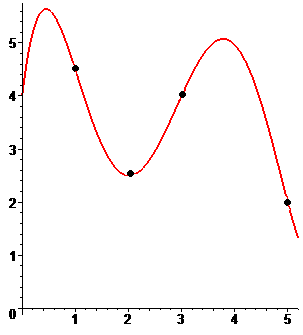
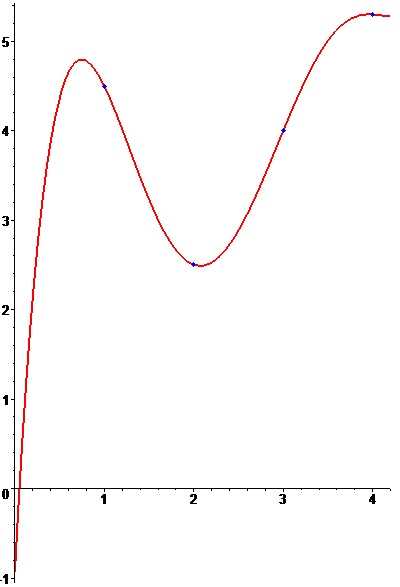
Многочлен в форме Ньютона, который строится на основании шести значений, представляет собой полином 5 степени. Результат построения полинома в форме Ньютона показан в графическом виде.
С помощью найденного полинома можно определить значение функции в любой точке заданного интервала. Определение промежуточных значений величины по имеющемуся дискретному набору известных значений называется «интерполяцией». В соответствии с условиями задачи полином в форме Ньютона в точке x =9,5 принимает следующее значение: L (9,5)= – 4,121. Из графика видно, что полученное значение не совпадает c о значением функции f ( x ) на величину абсолютной погрешности интерполяционной формулы Ньютона.
Интерполяционный полином в форме Ньютона часто оказывается удобным для проведения различных теоретических исследований в области вычислительной математики. Так, например, полином в форме Ньютона используются для интерполяции, а также для численного интегрирования таблично-заданной функцией.
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Интерполяция
Интерполяция или интерполирование — приближенное или точное нахождение какой-либо величины по известным отдельным значениям этой же величины, или других величин, с ней связанных.
Происхождение слова «интерполяция» ☞ ЗДЕСЬ.
Задача интерполяции решается в разных классах функций — полиномов алгебраических или тригонометрических, комбинаций экспонент; в классе рациональных функций. Начинаем изложение материала с самого простого случая —
Полиномиальная интерполяция
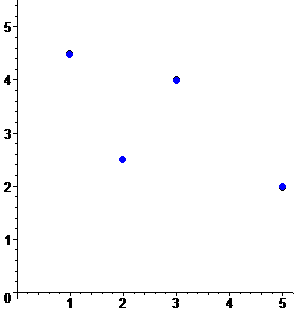
Все множество интерполяционных полиномов, принимающих значения по таблице, можно представить в виде
Решение ☞ ЗДЕСЬ.
Пусть имеется интерполяционная таблица
Пример. Интерполяционный полином для таблицы
Следовательно, применение вычислительных методов решения систем линейных уравнений — типа метода Гаусса — к системе с матрицей Вандермонда столкнется с необходимостью строгого контроля округлений. ♦
Практическое построение интерполяционного полинома производится альтернативными алгоритмами — посредством вспомогательных промежуточных представлений полинома в специальных, сравнительно просто вычисляемых, видах. Самыми распространенными являются формы Лагранжа и Ньютона.
Интерполяционый полином в форме Лагранжа
Пример. Построить интерполяционный полином по таблице
Рекурсивное вычисление коэффициентов
В настоящем пункте мы произведем «доводку» метода Лагранжа до коэффициентов интерполяционного полинома
Интерполяционный полином в форме Ньютона
Основной недостаток построения интерполяционного полинома по методу (в форме) Лагранжа заключается в том, что при добавлении в таблицу нового узла (новых результатов измерений), в формуле приходится пересчитывать все слагаемые. От этого недостатка свободен метод Ньютона, в котором добавление нового узла ведет к добавлению лишь одного слагаемого к построенному ранее полиному.
Теорема. Интерполяционный полином в форме Ньютона записывается в виде:
Применение полиномиальной интерполяции в задаче о разделении секрета
Обратная интерполяция
В одном из предшествующих ☝ пунктов решалcя следующий
Пример. Найти корни интерполяционного полинома, заданного таблицей
Интерполяционный полином Эрмита
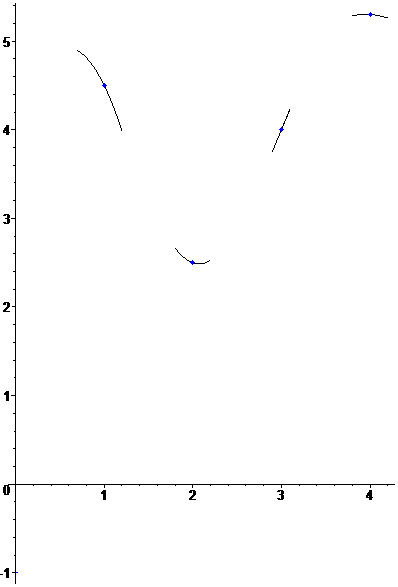
Пример. Построить интерполяционный полином по таблице
Построить уравнение «горки»: найти полином из условий
Следующий результат не очень связан с содержанием настоящего пункта, но надо было куда-то поместить.
Рациональная интерполяция
Первое решение задачи было предложено Коши в 1821 г. [9].
Теорема [Коши]. Обозначим:
Биографические заметки о Коши ☞ ЗДЕСЬ.
Другие примеры на применение теоремы Коши ☞ ЗДЕСЬ
Теорема Коши дает решение задачи в смысле «как правило». Дело в том, что задача рациональной интерполяции (в указанной постановке) не всегда разрешима.
Пример. Для таблицы
Альтернативный подход к решению задачи основывается на следующей теореме, развивающей результат К.Якоби [10,11]; он основан на идее из пункта ☝ о рекурсивном вычислении коэффициентов интерполяционного полинома.
Подробнее о методе Якоби (в том числе и об эффективном способе вычисления ганкелевых полиномов) ☞ ЗДЕСЬ.
Тригонометрическая интерполяция
Доказательство тривиально, если обратить внимание на аналогию с интерполяционным полиномом в форме Лагранжа. ♦
Теорема. Функция
Задача. Найти явные выражения для коэффициентов тригонометрического полинома из последней теоремы.
«Лобовое» решение аналогично решению задачи полиномиальной интерполяции — сведением ее к подходящей системе линейных уравнений.
Пример. Построить интерполяционный полином второго порядка по следующей таблице
Решение ☞ ЗДЕСЬ.
Для случая системы равноотстоящих узлов решение задачи значительно упрощается.
Подробное изложение теории тригонометрической интерполяции (и дискретного преобразования Фурье) ☞ ЗДЕСЬ
Интерполяция суммами экспонент
Материал настоящего пункта — сильная «выжимка» из [2]. Числовой пример — мой.
В отличие от рассмотренных выше задач алгебраической или тригонометрической интерполяции, поставленная задача является, во-первых, принципиально нелинейной относительно параметров, и, во-вторых, не всегда разрешимой.
Пример. Построить экспоненциальную функцию вида
Аппроксимация
Задача интерполяции является частным случаем более общей задачи аппроксимации функций, т.е. замены одной неизвестной или сложной для вычисления функции другой, более простой. Здесь существенно понятие «близости» функций, которое может быть различным в конкретных задачах.
Аппроксимация в случае недостоверности данных
Предположим теперь, что данные исходной таблицы не являются достоверными: значения обеих переменных подвержены воздействию случайных погрешностей одинакового порядка. Как воспользоваться этими данными для задачи аппроксимации? Мы рассмотрим здесь только две подобные задачи.
Координаты точки, для которой величина
Теорема 2 [3],[4]. Обозначим
$$ \begin
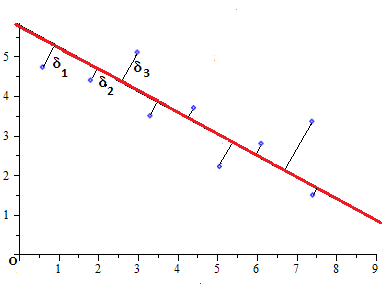
Метод наименьших квадратов
Пример. По методу наименьших квадратов построить уравнение прямой, аппроксимирующей множество точек плоскости, заданных координатами из таблицы
$$ \begin
Дальнейшее развитие идеологии МНК ☞ ЗДЕСЬ.
Многомерная интерполяция
Сложности: парадокс Крамера
Прямоугольная сетка
Задачи
Источники
[1]. Mycielski J. Polynomials with Preassigned Values at their Branching Points. The American Mathematical Monthly, 77 (8).1970, pp. 853-855
[2]. Henrici P. Applied and Computational Complex Analysis. V. 1. 1974. NY. Wiley
[4]. Hilbert D. Ein Beitrag zur Theorie des Legendreschen Polynoms. Acta Math. Bd.18, 1894, S.155-160
[5]. Форсайт Дж., Молер К. Численное решение систем линейных алгебраических уравнений. М. Мир. 1969
[6]. Линник Ю.В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. М.ГИФМЛ. 1958
[7]. Калинина Е.А., Утешев А.Ю. Теория исключения. Учеб. пособие. СПб.: НИИ Химии СПбГУ, 2002. 72 с.
[8]. Утешев А.Ю., Тамасян Г.Ш. К задаче полиномиального интерполирования с кратными узлами. Вестник СПбГУ. Серия 10. 2010. Вып. 3, С. 76-85. Текст (pdf) ☞ ЗДЕСЬ
[9]. Cauchy A.-L. Cours d’Analyse de l’École Royale Polytechnique: Part I: Analyse Algébrique. Paris, France: L’Imprimerie Royale, 1821, pt. 1.
[10]. Jacobi C.G.J. Űber die Darstellung einer Reihe gegebner Werthe durch eine gebrochne rationale Function. J.reine angew. Math. 1846. Bd. 30, S. 127-156
[11]. Утешев А.Ю., Боровой И.И. Решение задачи рациональной интерполяции с использованием ганкелевых полиномов. Вестник СПбГУ. Серия 10. 2016. Вып. 4, С. 31-43. Текст ☞ ЗДЕСЬ (pdf).
[12]. Pearson K. On lines and planes of closest fit to systems of points in space. Phil. Mag. 1901. V.2, pp. 559-572
Интерполяционный полином в форме Ньютона



Пусть, как и ранее, на отрезке [a, b] задана одномерная сетка
в узлах xi которой заданы значения yi = f(xi), i = 0, 1, 2, …, n – соответствующие значения функции f(x).
Интерполяционный полином в форме Ньютона для x Î (a, b) может быть записан в виде
или в более компактной форме
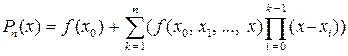
Разделенные разности для табличных данных рассчитываются следующим образом:
· разделенные разности 1-го порядка по формуле
· разделенные разности 2-го порядка через разделенные разности 1-го порядка:
В общем случае разделенные разности k-го порядка определяются
через разделенные разности (k – 1)-го порядка:
Учитывая связь разделенных разностей с производными таблично заданной функции f(x), интерполяционный полином в форме Ньютона можно считать разностной аппроксимацией формулы Тейлора для функции f(x).
Нетрудно показать, что для интерполяционного полинома Pn(x)
в форме Ньютона выполняются условия интерполяции по узлам сетки:
Кроме того, можно убедиться в том, что интерполяционный полином в форме Ньютона только по форме отличается от интерполяционного полинома в форме Лагранжа, представляя собой на заданной сетке один и тот же интерполяционный полином. Поскольку, как было отмечено ранее, интерполяционный полином единственен, то последнее утверждение является вполне естественным и должно выполняться для любых форм представления этого полинома, если сетка и значения функции не изменяются.
В соответствии с соотношением (3.3.1) процесс интерполяции таблично заданной на отрезке [a, b] функции в заданную точку x * Î (a, b)
с помощью интерполяционного полинома в форме Ньютона можно представить в виде следующего алгоритма:
0. На отрезке [a, b] задать одномерную сетку
2. Вычислить разделенные разности k-го порядка
6. Если k £ n, перейти к выполнению п. 2.
Отметим некоторые характерные особенности использования интерполяционного полинома в форме Ньютона для интерполяции табличных данных.
1. Вычисления разделенных разностей в п. 3 приведенного алгоритма удобно производить, записывая их в таблицу, аналогичную табл. 3.3.1 для сетки с девятью узлами.
| № узла | xi | f(xi) | f(xi, xi+1) | f(xi, xi+1, xi+2) | f(xi, xi+1, xi+2, xi+3) | … | f(xi, xi+1, xi+2, …, xi+n) |
| x0 | f(x0) | … | |||||
| f(x0, x1) | … | ||||||
| x1 | f(x1) | f(x0, x1, x2) | … | ||||
| f(x1, x2) | f(x0, x1, x2, x3) | … | |||||
| x2 | f(x2) | f(x1, x2, x3) | … | ||||
| f(x2, x3) | f(x1, x2, x3, x4) | … | |||||
| x3 | f(x3) | f(x2, x3, x4) | … | ||||
| f(x3, x4) | f(x2, x3, x4, x5) | … | |||||
| x4 | f(x4) | f(x3, x4, x5) | … | f(x0, x1, x2,…, x8) | |||
| f(x4, x5) | f(x3, x4, x5, x6) | … | |||||
| x5 | f(x5) | f(x4, x5, x6) | … | ||||
| f(x5, x6) | f(x4, x5, x6, x7) | … | |||||
| x6 | f(x6) | f(x5, x6, x7) | … | ||||
| f(x6, x7) | f(x5, x6, x7, x8) | … | |||||
| x7 | f(x7) | f(x6, x7, x8) | … | ||||
| f(x7, x8) | … | ||||||
| x8 | f(x8) | … |
Разделенные разности образуют в таблице своеобразный треугольник. При расчете значения Pn(x * ) используются разделенные разности, находящиеся как бы на верхней стороне этого треугольника (они выделены в таблице жирным шрифтом).
2. Использование интерполяционного полинома в форме Ньютона оказывается удобным, например, когда появляются дополнительные узлы. Так, если добавлен один новый узел, то в формуле (3.3.1) для интерполяционного полинома в форме Ньютона добавится еще одно слагаемое, которое нужно прибавить к уже рассчитанной сумме предыдущих слагаемых (они, очевидно, не изменяются). Для расчета значения дополнительного слагаемого в нижней части таблицы для конечных разностей добавляется еще одна строка, соответствующая этому узлу. Ранее рассчитанные разности пересчитывать не нужно, необходимо лишь определить дополнительно значения тех разделенных разностей, которые будут находиться на нижней стороне нового «треугольника» разделенных разностей.
3. Формулу (3.3.1) для интерполяционного полинома в форме Ньютона можно записать для любого способа упорядочивания узлов. Так, например, при упорядочивании узлов в обратном порядке(xn, xn – 1, xn – 2, …, x2, x0) формула (3.3.1) для представления интерполяционного полинома в форме Ньютона примет вид
Если интерполяционный полином в форме Ньютона Pn(x) определяется по формуле (3.3.1), его называют интерполяционным полиномом для интерполирования вперед (или для интерполирования в начале таблицы). Этот полином целесообразно использовать, когда точка x * находится в начале таблицы.
Если Pn(x) определяется по формуле (3.3.3), его называют интерполяционным полиномом для интерполирования назад (или для интерполирования в конце таблицы). Его целесообразно использовать, когда точка x * находится в нижней части таблицы.
4. Как уже говорилось, не рекомендуется использовать интерполяционные полиномы выше 6-го порядка: в этом случае при их построении может быть использовано в совокупности не более семи узлов сетки, находящихся на оси Ох с обеих сторон от точки x * Î (a, b).
5. Оценка точности интерполяции с помощью интерполяционного полинома в форме Ньютона совпадает с оценкой точности интерполяции, приведенной для интерполяционного полинома в форме Лагранжа, поскольку оба этих полинома представляют собой один и тот же интерполяционный полином и различаются только формой записи:
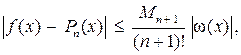
где Mn + 1 – верхняя граница значения модуля (n + 1)-й производной функции f(x) на отрезке [a, b].
В соответствии с (3.3.4) погрешность интерполяции будет равна нулю, если интерполируемая функция представляет собой полином, степень которого не превышает n.