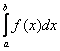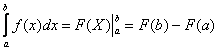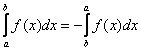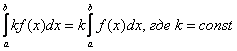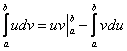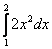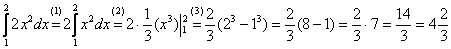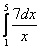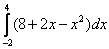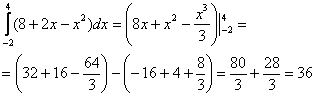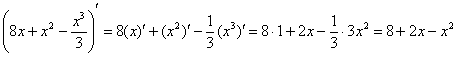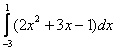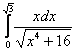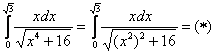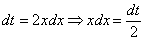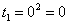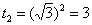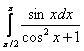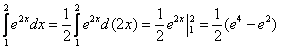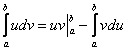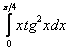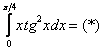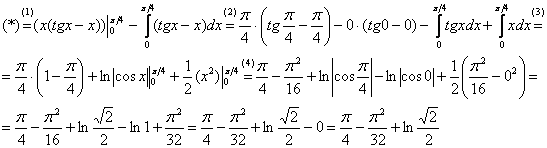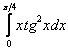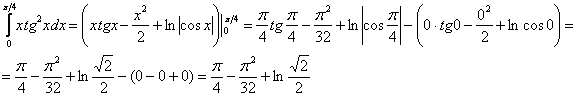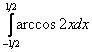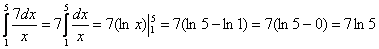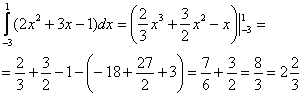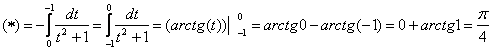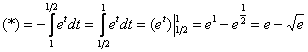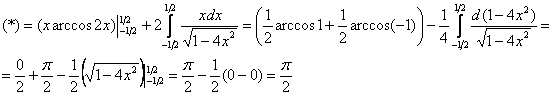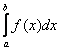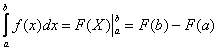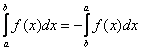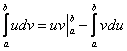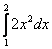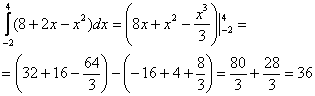Как решать определенные интегралы
Как решать определенные интегралы
Вычисление определенного интеграла. Формула Ньютона-Лейбница
Решение прикладных задач сводится к вычислению интеграла, но не всегда это возможно сделать точно. Иногда необходимо знать значение определенного интеграла с некоторой степенью точности, к примеру, до тысячной.
Существуют задачи, когда следовало бы найти приближенное значение определенного интеграла с необходимой точностью, тогда применяют численное интегрирование такое, как метод Симпосна, трапеций, прямоугольников. Не все случаи позволяют вычислить его с определенной точностью.
Данная статья рассматривает применение формулы Ньютона-Лейбница. Это необходимо для точного вычисления определенного интеграла. Будут приведены подробные примеры, рассмотрены замены переменной в определенном интеграле и найдем значения определенного интеграла при интегрировании по частям.
Формула Ньютона-Лейбница
Данную формулу считают основной формулой интегрального исчисления.
Чтобы произвести доказательство этой формулы, необходимо использовать понятие интеграла с имеющимся переменным верхним пределом.
Произведем вычисление F ( a ) с использованием первого свойства определенного интеграла. Тогда получаем, что
Произвести вычисление определенного интеграла ∫ 1 3 x 2 d x по формуле Ньютона-Лейбница.
Ответ: ∫ 1 3 x 2 d x = 26 3
Необходимо взять первообразную при С = 0 и применить формулу Ньютона-Лейбница. Тогда получим выражение вида
Производим переход к вычислению второго интеграла.
Перед использованием формулы Ньютона-Лейбница нужно точно знать о существовании определенного интеграла.
Замена переменной в определенном интеграле
Отсюда произведем вычисления по формуле Ньютона-Лейбница и вычислим определенный интеграл. Получаем, что
Интегрирование по частям при вычислении определенного интеграла
Решение примера можно выполнить другим образом.
Найти множество первообразных функции x · sin x 3 + π 6 при помощи интегрирования по частям с применением формулы Ньютона-Лейбница:
Ответ: ∫ x · sin x x 3 + π 6 d x = 3 π 4 + 9 3 2
Определенный интеграл. Примеры решений
И снова здравствуйте. На данном уроке мы подробно разберем такую замечательную вещь, как определенный интеграл. На этот раз вступление будет кратким. Всё. Потому что снежная метель за окном.
Для того чтобы научиться решать определенные интегралы необходимо:
1) Уметь находить неопределенные интегралы.
2) Уметь вычислить определенный интеграл.
Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений. Кроме того, есть pdf-курсы для сверхбыстрой подготовки – если у вас в запасе буквально день, пол дня.
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования.
Нижний предел интегрирования стандартно обозначается буквой 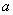
Верхний предел интегрирования стандартно обозначается буквой 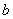
Отрезок 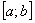
Прежде чем мы перейдем к практическим примерам, небольшое faq по определенному интегралу.
Что такое определенный интеграл? Считаю немного преждевременным рассказать про разбиения отрезка и предел интегральных сумм, поэтому пока я скажу, что определенный интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число.
Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла.
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.
Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница:
Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию 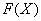
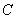
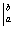
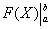
2) Подставляем значение верхнего предела в первообразную функцию: 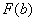
3) Подставляем значение нижнего предела в первообразную функцию: 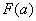
4) Рассчитываем (без ошибок!) разность 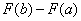
Всегда ли существует определенный интеграл? Нет, не всегда.
Например, интеграла 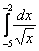
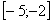
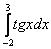
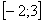
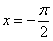
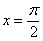
Для того чтобы определенный интеграл вообще существовал, достаточно чтобы подынтегральная функция была непрерывной на отрезке интегрирования.
Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования. По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?». В упрощенном варианте ситуация выглядит примерно так:
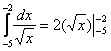
Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен интеграл вроде 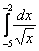
! Примечание: в последнем случае слово «определённого» опускать нельзя, т.к. интеграл с точечными разрывами разбивается на несколько, в данном случае на 3 несобственных интеграла, и формулировка «данного интеграла не существует» становится некорректной.
Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим отведена отдельная лекция.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может, и такая ситуация реально встречается на практике.
Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.
В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:
Например, в определенном интеграле перед интегрированием 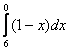
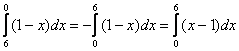
Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:
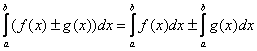
В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.
Для определенного интеграла справедлива формула интегрирования по частям:
Вычислить определенный интеграл
Решение:
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью самой популярной формулы 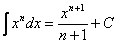
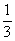
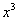
(3) Используем формулу Ньютона-Лейбница 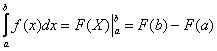
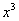
Вычислить определенный интеграл
Это пример для самостоятельно решения, решение и ответ в конце урока.
Немного усложняем задачу:
Вычислить определенный интеграл
Решение:
(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница: 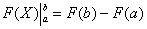
СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряю на третьем слагаемом: 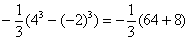
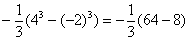
Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, я сам привык решать подобные интегралы так:
Здесь я устно использовал правила линейности, устно проинтегрировал по таблице. У меня получилась всего одна скобка с отчёркиванием пределов: 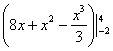
Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, но лично мне всё равно – обыкновенные дроби я считаю на калькуляторе.
Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту-чайнику лучше использовать первый способ, при «моём» способе решения точно где-нибудь потеряется знак.
Однако несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная 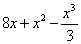
Совет: перед тем, как использовать формулу Ньютона-Лейбница, полезно провести проверку: а сама-то первообразная найдена правильно?
Так, применительно к рассматриваемому примеру: перед тем, как в первообразную функцию 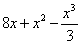
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден верно. Теперь можно и формулу Ньютона-Лейбница применить.
Такая проверка будет не лишней при вычислении любого определенного интеграла.
Вычислить определенный интеграл
Это пример для самостоятельно решения. Попробуйте решить его коротким и подробным способом.
Замена переменной в определенном интеграле
Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла. Таким образом, если с заменами у Вас не очень, следует внимательно ознакомиться с уроком Метод замены в неопределенном интеграле.
В этом параграфе нет ничего страшного или сложного. Новизна состоит в вопросе, как поменять пределы интегрирования при замене.
В примерах я постараюсь привести такие типы замен, которые еще нигде не встречались на сайте.
Вычислить определенный интеграл
Главный вопрос здесь вовсе не в определенном интеграле, а в том, как правильно провести замену. Смотрим в таблицу интегралов и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: 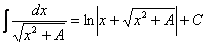
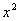
Сначала готовим наш интеграл к замене:
Из вышеуказанных соображений совершенно естественно напрашивается замена: 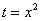
Таким образом, в знаменателе будет всё хорошо: 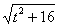
Выясняем, во что превратится оставшаяся часть 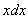
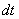
По сравнению с заменой в неопределенном интеграле у нас добавляется дополнительный этап.
Находим новые пределы интегрирования.
Это достаточно просто. Смотрим на нашу замену 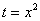
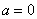
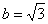
Сначала подставляем в выражение замены 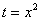
Потом подставляем в выражение замены 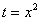
Готово. И всего-то лишь…
(1) В соответствии с заменой записываем новый интеграл с новыми пределами интегрирования.
(2) Это простейший табличный интеграл, интегрируем по таблице. Константу 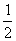
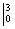
(3) Используем формулу Ньютона-Лейбница 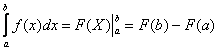
Ответ стремимся записать в максимально компактном виде, здесь я использовал свойства логарифмов.
Ещё одно отличие от неопределенного интеграла состоит в том, что, после того, как мы провели замену, никаких обратных замен проводить не надо.
А сейчас пара примеров для самостоятельного решения. Какие замены проводить – постарайтесь догадаться самостоятельно.
Вычислить определенный интеграл
Вычислить определенный интеграл
Это примеры для самостоятельного решения. Решения и ответы в конце урока.
И в заключение параграфа пара важных моментов, разбор которых появился благодаря посетителям сайта. Первый из них касается правомерности замены. В некоторых случаях её проводить нельзя! Так, Пример 6, казалось бы, разрешим с помощью универсальной тригонометрической подстановки 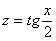
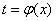
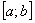
В другом электронном письме поступил следующий вопрос: «А нужно ли менять пределы интегрирования, когда мы подводим функцию под знак дифференциала?». Сначала я хотел «отмахнуться от ерунды» и автоматически ответить «конечно, нет», но затем задумался о причине появления такого вопроса и вдруг обнаружил, что информации-то не хватает. А ведь она, пусть и очевидна, но очень важнА:
Если мы подводим функцию под знак дифференциала, то менять пределы интегрирования не нужно! Почему? Потому что в этом случае нет фактического перехода к новой переменной. Например:
И здесь подведение гораздо удобнее академичной замены 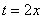
Большое спасибо за ваши письма!
Метод интегрирования по частям в определенном интеграле
Здесь новизны еще меньше. Все выкладки статьи Интегрирование по частям в неопределенном интеграле в полной мере справедливы и для определенного интеграла.
Плюсом идёт только одна деталь, в формуле интегрирования по частям добавляются пределы интегрирования:
Формулу Ньютона-Лейбница здесь необходимо применить дважды: для произведения 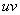
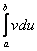
Тип интеграла для примера я опять подобрал такой, который еще нигде не встречался на сайте. Пример не самый простой, но очень и очень познавательный.
Вычислить определенный интеграл
Решаем.
Интегрируем по частям:
У кого возникли трудности с интегралом 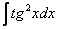
(1) Записываем решение в соответствии с формулой интегрирования по частям.
(2) Для произведения 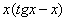
(3) Берем два оставшихся интеграла. Интеграл 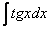
(4) Применяем формулу Ньютона-Лейбница для двух найденных первообразных.
Далее ответ доводится «до ума». Повторюсь, будьте ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫ при подстановках и заключительных вычислениях. Здесь допускают ошибки чаще всего.
Если честно, я недолюбливаю формулу 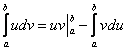
Вычислить определенный интеграл
На первом этапе я нахожу неопределенный интеграл:
Интегрируем по частям:
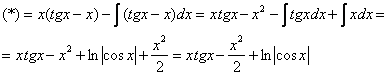
Первообразная функция найдена. Константу 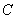
В чём преимущество такого похода? Не нужно «таскать за собой» пределы интегрирования, действительно, замучаться можно десяток раз записывать мелкие значки пределов интегрирования
На втором этапе я провожу проверку (обычно на черновике).
Тоже логично. Если я неправильно нашел первообразную функцию, то неправильно решу и определенный интеграл. Это лучше выяснить немедленно, дифференцируем ответ:
Получена исходная подынтегральная функция, значит, первообразная функция найдена верно.
Третий этап – применение формулы Ньютона-Лейбница:
И здесь есть существенная выгода! В «моём» способе решения гораздо меньший риск запутаться в подстановках и вычислениях – формула Ньютона-Лейбница применяется всего лишь один раз. Если чайник решит подобный интеграл по формуле 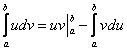
Рассмотренный алгоритм решения можно применить для любого определенного интеграла.
Уважаемый студент, распечатай и сохрани:
Что делать, если дан определенный интеграл, который кажется сложным или не сразу понятно, как его решать?
1) Сначала находим неопределенный интеграл (первообразную функцию). Если на первом же этапе случился облом, дальше рыпаться с Ньютоном и Лейбницем бессмысленно. Путь только один – повышать свой уровень знаний и навыков в решении неопределенных интегралов.
2) Проверяем найденную первообразную функцию дифференцированием. Если она найдена неверно, третий шаг будет напрасной тратой времени.
3) Используем формулу Ньютона-Лейбница. Все вычисления проводим ПРЕДЕЛЬНО ВНИМАТЕЛЬНО – тут самое слабое звено задания.
И, на закуску, интеграл для самостоятельного решения.
Вычислить определенный интеграл
Решение и ответ где-то рядом.
Следующий рекомендуемый урок по теме – Как вычислить площадь фигуры с помощью определенного интеграла? Там речь пойдет о геометрическом смысле определенного интеграла. Дополнительные материалы по определенному интегралу также можно найти в статье Эффективные методы вычисления определенных интегралов. Данный урок содержит ряд очень важных технических приёмов и позволит существенно повысить навыки вычисления определенного интеграла.
Решения и ответы:
Пример 2: Решение:
Пример 4: Решение:
Пример 6: Решение:
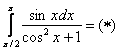
Проведем замену переменной: 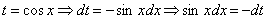
Новые переделы интегрирования: 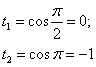
Примечания: В рассмотренном интеграле – как раз тот случай, когда уместно применить свойство определенного интеграла 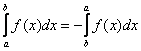
Если не совсем понятно, почему из арктангенса можно вынести минус, рекомендую обратиться к методическому материалу Графики и свойства элементарных функций.
Пример 7: Решение: 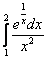
Замена: 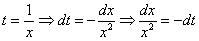
Новые пределы интегрирования: 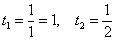
Пример 9: Решение: 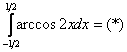
Интегрируем по частям: 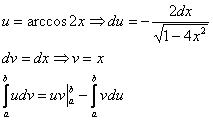
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys
Вычисление определённых интегралов: базовые алгоритмы
В этой публикации описаны простейшие методы вычисления интегралов функций от одной переменной на отрезке, также называемые квадратурными формулами. Обычно эти методы реализованы в стандартных математических библиотеках, таких как GNU Scientific Library для C, SciPy для Python и других. Публикация имеет целью продемонстрировать, как эти методы работают «под капотом», и обратить внимание на некоторые вопросы точности и производительности алгоритмов. Также хотелось бы отметить связь квадратурных формул и методов численного интегрирования обыкновенных дифференциальных уравнений, о которых хочу написать ещё одну публикацию.
Определение интеграла
Интегралом (по Риману) от функции на отрезке
называется следующий предел:
где — мелкость разбиения,
,
,
— произвольное число на отрезке
.
Если интеграл от функции существует, то значение предела одно и то же вне зависимости от разбиения, лишь бы оно было достаточно мелким. 
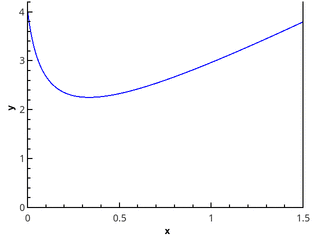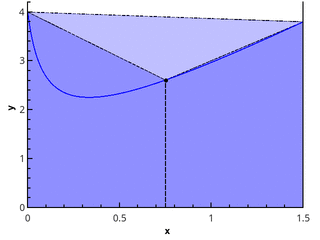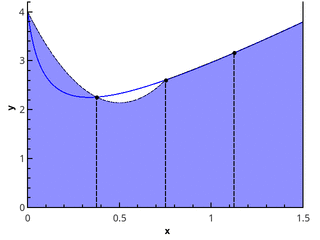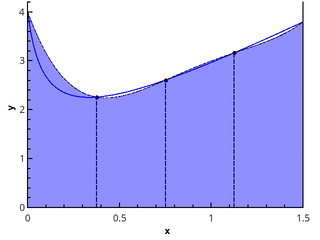
Более наглядно геометрическое определение — интеграл равен площади криволинейной трапеции, ограниченной осью 0x, графиком функции и прямыми x = a и x = b (закрашенная область на рисунке).
Квадратурные формулы
Определение интеграла (1) можно переписать в виде
где — весовые коэффициенты, сумма которых должна быть равна 1, а сами коэффициенты — стремиться к нулю при увеличении числа
точек, в которых вычисляется функция.
Выражение (2) — основа всех квадратурных формул (т.е. формул для приближенного вычисления интеграла). Задача состоит в том, чтобы выбрать точки и веса
таким образом, чтобы сумма в правой части приближала требуемый интеграл как можно точнее.
Вычислительная задача
Задана функция , для которой есть алгоритм вычисления значений в любой точке отрезка
(имеются в виду точки, представимые числом с плавающей точкой — никаких там функций Дирихле!).
Требуется найти приближённое значение интеграла .
Решения будут реализованы на языке Python 3.6.
Для проверки методов используется интеграл .
Кусочно-постоянная аппроксимация
Идейно простейшие квадратурные формулы возникают из применения выражения (1) «в лоб»:
Т.к. от метода разбиения отрезка точками и выбора точек
значение предела не зависит, то выберем их так, чтобы они удобно вычислялись — например, разбиение возьмём равномерным, а для точек вычисления функции рассмотрим варианты: 1)
; 2)
; 3)
.
Получаем методы левых прямоугольников, правых прямоугольников и прямоугольников со средней точкой, соответственно.
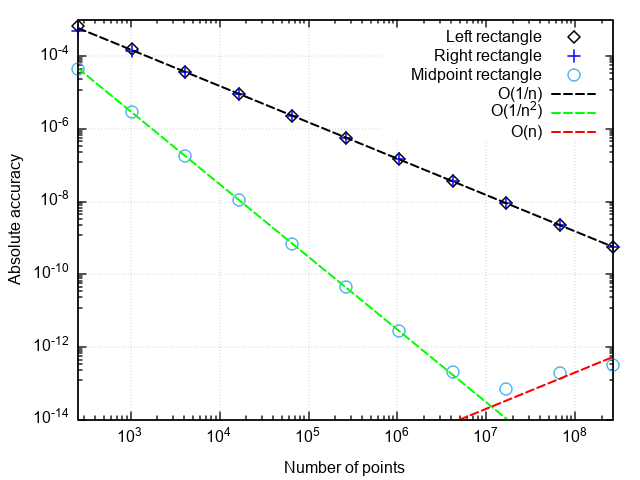
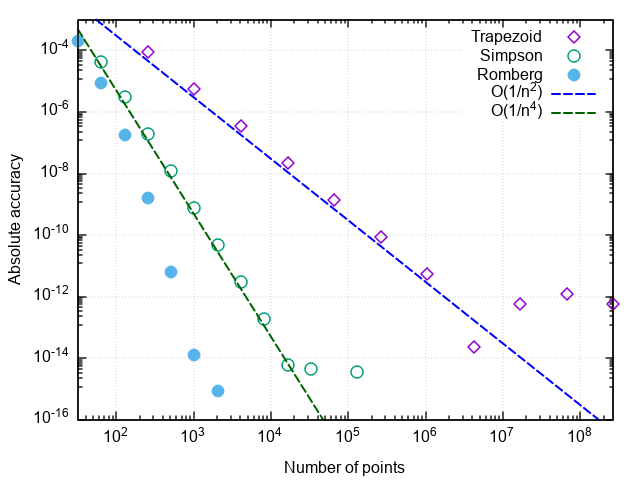
Для анализа производительности квадратурных формул построим график погрешности в координатах «число точек — отличие численного результата от точного».
Что можно заметить:
Кусочно-линейная аппроксимация
Следующий логический шаг — аппроксимировать интегрируемую функцию на каждом из подотрезков линейной функцией, что даёт квадратурную формулу трапеций:
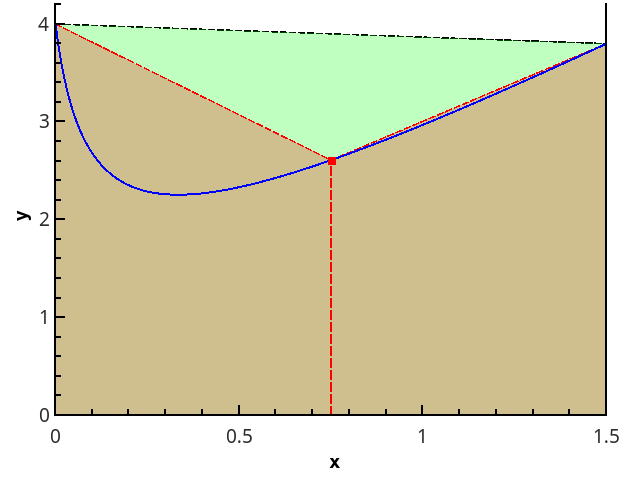
Иллюстрация метода трапеций для n=1 и n=2.
В случае равномерной сетки длины всех отрезков разбиения равны, и формула имеет вид
Построив график ошибки от числа точек разбиения, убеждаемся, что метод трапеций тоже имеет второй порядок аппроксимации и вообще даёт результаты, слабо отличающиеся от метода прямоугольников со средней точкой (в дальнейшем — просто метод прямоугольников).
Контроль точности вычисления
Задание в качестве входного параметра числа точек разбиения не слишком практично, поскольку обычно требуется вычислить интеграл не с заданной плотностью разбиения, а с заданной погрешностью. Если подынтегральная функция известна наперёд, то можно оценить погрешность заранее и выбрать такой шаг интегрирования, чтобы заданная точность заведомо достигалась. Но так редко бывает на практике (и вообще, не проще ли при известной наперёд функции и сам интеграл протабулировать наперёд?), поэтому необходима процедура автоматической подстройки шага под заданную погрешность.
Как это реализовать? Один из простых методов оценки погрешности — правило Рунге — разность значений интегралов, рассчитанных по n и 2n точкам, даёт оценку погрешности: . Метод трапеций удобнее для удвоения мелкости разбиения, чем метод прямоугольников с центральной точкой. При расчёте методом трапеций для удвоения числа точек нужны новые значения функции только в серединах отрезков предыдущего разбиения, т.е. предыдущее приближение интеграла можно использовать для вычисления следующего.
Отсюда получаем следующий код для метода трапеций с контролем точности:
С таким подходом подынтегральная функция не будет вычисляться по нескольку раз в одной точке, и все вычисленные значения используются для окончательного результата.
Но нельзя ли при том же количестве вычислений функции добиться более высокой точности? Оказывается, что можно, есть формулы, работающие точнее метода трапеций на той же самой сетке.
Кусочно-параболическая аппроксимация

Иллюстрация кусочно-параболического приближения на 3 и 5 точках (n=2 и n=3).
Приближая интеграл от функции на каждом из отрезков [xk;xk+2] интегралом от параболической аппроксимации на этом отрезке и считая точки равномерно распределенными (xk+1=xk+h), получаем формулу Симпсона:
Из формулы (4) напрямую получается «наивная» реализация метода Симпсона:
Для оценки погрешности можно использовать точно так же вычисление интеграла с шагами h и h/2 — но вот незадача, при вычислении интеграла с более мелким шагом результат предыдущего вычисления придётся отбросить, хотя половина новых вычислений функции будет в тех же точках, что и раньше.
Бесполезной траты машинного времени, к счастью, можно избежать, если реализовать метод Симпсона более хитроумным образом. Присмотревшись повнимательнее, заметим, что интеграл по формуле Симпсона может быть представлен через два интеграла по формуле трапеций с разными шагами. Яснее всего это видно на базовом случае аппроксимации интеграла по трём точкам :
Таким образом, если реализовать процедуру уменьшения шага вдвое и хранить два последних вычисления методом трапеций, метод Симпсона с контролем точности реализуется более эффективно.
Сравним эффективность метода трапеций и парабол:
Как видим, обоими методами ответ можно получть с достаточно высокой точностью, но количество вызовов подынтегральной функции разительно отличается — метод более высокого порядка эффективнее в 32 раза!
Построив график погрешности интегрирования от числа шагов, можно убедиться, что порядок аппроксимации формулы Симпсона равен четырём, т.е. ошибка численного интегрирования (а интегралы от кубических многочленов с помощью этой формулы вычисляются с точностью до ошибок округления при любом чётном n>0!).
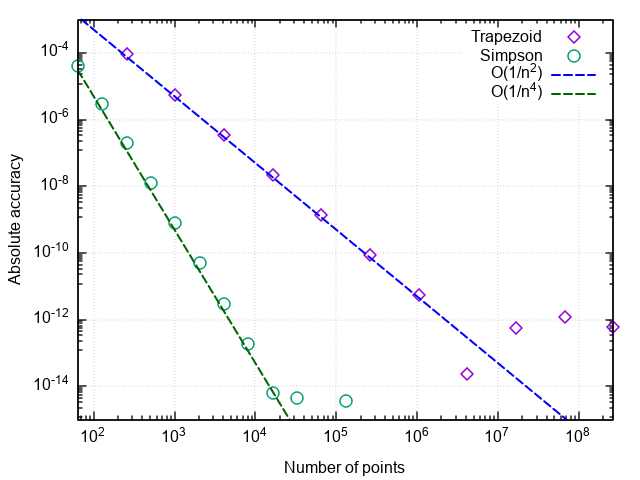
Отсюда и возникает такой рост эффективности по сравнению с простой формулой трапеций.
Что дальше?
Дальнейшая логика повышения точности квадратурных формул, в целом, понятна — если функцию продолжать приближать многочленами всё более высокой степени, то и интеграл от этих многочленов будет всё точнее приближать интеграл от исходной функции. Этот подход называется построением квадратурных формул Ньютона-Котеса. Известны формулы вплоть до 8 порядка аппроксимации, но выше среди весовых коэффициентов wi в (2) появляются знакопеременные члены, и формулы при вычислениях теряют устойчивость.
Попробуем пойти другим путём. Ошибка квадратурной формулы представляется в виде ряда по степеням шага интегрирования h. Замечательное свойство метода трапеций (и прямоугольников со средней точкой!) в том, что для неё этот ряд состоит только из чётных степеней:
На нахождении последовательных приближений к этому разложению основана экстраполяция Ричардсона: вместо того, чтобы приближать подынтегральную функцию многочленом, по рассчитанным приближениям интеграла строится полиномиальная аппроксимация, которая при h=0 должна давать наилучшее приближение к истинному значению интеграла.
Разложение ошибки интегрирования по чётным степеням шага разбиения резко ускоряет сходимость экстраполяции, т.к. для аппроксимации порядка 2n нужно всего n значений интеграла методом трапеций.
Если считать, что каждое последующее слагаемое меньше предыдущего, то можно последовательно исключать степени h, имея приближения интеграла, рассчитанные с разными шагами. Поскольку приведённая реализация легко позволяет дробить разбиение вдвое, удобно рассматривать формулы для шагов h и h/2.
Легко показать, что исключение старшего члена погрешности формулы трапеций в точности даст формулу Симпсона:
Повторяя аналогичную процедуру для формулы Симпсона, получаем:
Если продолжить, вырисовывается такая таблица:
| 2 порядок | 4 порядок | 6 порядок | . |
|---|---|---|---|
| I0,0 | |||
| I1,0 | I1,1 | ||
| I2,0 | I2,1 | I2,2 | |
| . | . | . |
В первом столбце стоят интегралы, вычисленные методом трапеций. При переходе от верхней строки вниз разбиение отрезка становится вдвое мельче, а при переходе от левого столбца вправо повышается порядок аппроксимации интеграла (т.е. во втором столбце находятся интегралы по методу Симпсона и т.д.).
Элементы таблицы, как можно вывести из разложения (5), связаны рекуррентным соотношением:
Погрешность приближения интеграла можно оценить по разности формул разных порядков в одной строке, т.е.
Применение экстраполяции Ричардсона вместе с интегрированием методом трапеций называется методом Ромберга. Если метод Симпсона учитывает два предыдущих значения по методу трапеций, то метод Ромберга использует все ранее вычисленные методом трапеций значения для получения более точной оценки интеграла.
Дополнительный метод добавляется в класс Quadrature
Проверим, как работает аппроксимация высокого порядка:
Убеждаемся, что, по сравнению с методом парабол, число вызовов подынтегральной функции снизилось ещё в 8 раз. При дальнейшем увеличении требуемой точности преимущества метода Ромберга проявляются ещё заметнее:
Некоторые замечания
Замечание 2. Если метод сходится при задании некоторой точности, это не означает, что вычисленное значение интеграла имеет ту же самую точность. В первую очередь, это относится к случаям, когда задаваемая погрешность близка к машинной точности.
Замечание 3. Хотя метод Ромберга для ряда функций работает почти магическим образом, он предполагает наличие у подынтегральной функции ограниченных производных высоких порядков. Это значит, что для функций с изломами или разрывами он может оказаться хуже простых методов. Например, проинтегрируем f(x)=|x|:
7 второе слагаемое в (6) теряет точность после приведения порядков при сложении чисел с плавающей точкой, и повышение порядка аппроксимации может вести к накоплению ошибки округления.
Замечание 5. Желающие могут ради интереса применить описанные методы для нахождения интеграла и эквивалентного ему
. Как говорится, почувствуйте разницу.
Заключение
Представлено описание и реализация базовых методов численного интегрирования функций на равномерной сетке. Продемонстрировано, как с помощью несложной модификации получить на базе метода трапеций класс квадратурных формул по методу Ромберга, что значительно ускоряет сходимость численного интегрирования. Метод хорошо работает для интегрирования «обычных» функций, т.е. слабо меняющихся на отрезке интегрирования, не имеющих особенностей на краях отрезка (см. Замечание 5), быстрых осцилляций и т.д.
Продвинутые методы численного интегрирования для более сложных случаев можно найти в книгах из списка литературы (в [3] — с примерами реализации на C++).
Определённый интеграл и методы его вычисления
В каждой главе будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Понятие определённого интеграла и формула Ньютона-Лейбница
Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где 
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,

Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:

Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому
Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.
При a = b по определению принимается
Для того чтобы потренироваться в нахождении определённых интегралов, потребуется таблица основных неопределённых интегралов и пособие «Действия со степенями и корнями«.
Пример 1. Вычислить определённый интеграл
Решение. Сначала найдём неопределённый интеграл:
Применяя формулу Ньютона-Лейбница к первообразной
(при С = 0), получим
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2. Вычислить определённый интеграл
Решение. Используя формулу
Найти определённый интеграл самостоятельно, а затем посмотреть решение
Пример 3. Найти определённый интеграл

Пример 4. Найти определённый интеграл

Свойства определённого интеграла
Теорема 1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.
Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница:
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.

Пусть F(x) – первообразная для f(x). Для f(t) первообразной служит та же функция F(t), в которой лишь иначе обозначена независимая переменная. Следовательно,
На основании формулы (39) последнее равенство означает равенство интегралов
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла, т.е.

Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.

Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если

Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е.

Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке 

Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9. Если верхний предел интегрирования больше нижнего и функции 

можно почленно интегрировать, т.е.

Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Пример 5. Вычислить определённый интеграл
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим
Определённый интеграл с переменным верхним пределом
Пусть f(x) – непрерывная на отрезке [a, b] функция, а F(x) – её первообразная. Рассмотрим определённый интеграл


а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х, которую обозначим через Ф(х), т.е.

Докажем, что функция Ф(х) является первообразной для f(x) = f(t). Действительно, дифференцируя Ф(х), получим
Функция Ф(х) – одна из бесконечного множества первообразных для f(x), а именно та, которая при x = aобращается в нуль. Это утверждение получается, если в равенстве (48) положить x = aи воспользоваться теоремой 1 предыдущего параграфа.
Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
При выводе формулы интегрирования по частям было получено равенство u dv = d (uv) – v du. Проинтегрировав его в пределах от a до b и учитывая теорему 4 параграфа этой статьи о свойствах определённого интеграла, получим
Как это следует из теоремы 2 параграфа о свойствах неопределённого интеграла, первый член в правой части равен разности значений произведения uv при верхнем и нижнем пределах интегрирования. Записав эту разность кратко в виде
получаем формулу интегрирования по частям для вычисления определенного интеграла:

Пример 6. Вычислить определённый интеграл
Найти определённый интеграл по частям самостоятельно, а затем посмотреть решение
Пример 7. Найти определённый интеграл

Пример 8. Найти определённый интеграл

Перейдём к вычислению определённого интеграла методом замены переменной. Пусть
где, по определению, F(x) – первообразная для f(x). Если в подынтегральном выражении произвести замену переменной
то в соответствии с формулой (16) можно записать
В этом выражении
первообразная функция для
принимает соответственно значения aи b, т.е.
Но, согласно формуле Ньютона-Лейбница, разность F(b) – F(a) есть

Это и есть формула перехода к новой переменной под знаком определённого интеграла. С её помощью определённый интеграл
после замены переменной
преобразуется в определённый интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются новыми пределами 

поставить значения x = aи x = b, т.е. решить уравнения
относительно 

При вычислении определённого интеграла методом замены переменной часто бывает удобно выражать не старую переменную как функцию новой, а, наоборот, новую – как функцию старой.
Пример 9. Вычислить определённый интеграл
Решение. Произведём замену переменной, полагая
Найдём новые пределы интегрирования. Подстановка значений x = 4 и x = 5 в уравнение
Используя теперь формулу (50), получим
После замены переменной мы не возвращались к старой переменной, а применили формулу Ньютона-Лейбница к полученной первообразной.
Найти определённый интеграл заменой переменной самостоятельно, а затем посмотреть решение
Пример 10. Найти определённый интеграл

Пример 11. Найти определённый интеграл

Правила решения интегралов для студентов
Обновлено: 02 Октября 2021
Интеграл является одним из наиболее важных понятий в математическом анализе. Его применяют в алгебре для расчета площади под кривой, преодоленного пути в процессе неравномерного движения, массы, которой обладает неоднородное тело и решения других подобных задач. С помощью интеграла вычисляют функцию по известной производной.
Интегралы для чайников — базовые понятия
Понятие интеграла в теории основано на нахождении непрерывной функции. Для начала следует ознакомиться с этим термином.
Непрерывная функция F(х) представляет собой первообразную функции f(х) на понятном промежутке х при условии, что F(х)=f(х).
Процедура поиска первообразной функции f(х) представляет собой операцию интегрирования в определенном порядке.
Интеграл в кратком смысле является аналогом суммы для бесконечного числа бесконечно малых слагаемых.
Неопределенный интеграл
Неопределенным интегралом называют комплекс всех первообразных функции f(х).
В легком виде формулу для расчета неопределенного интеграла можно записать в такой форме:
В неопределенный интеграл включен спектр первообразных, так как имеется постоянная интегрирования. Дифференциалом называют произвольное, бесконечно малое приращение переменной величины. Среди основных свойств неопределенного интеграла можно отметить такие пояснения:
Табличная форма неопределенных интегралов в виде \(\int f(x)dx=F(x)+C\) имеет вид:
Определенный интеграл
Определенным интегралом называют приращение одной из первообразных функции f(х), соответствующих отрезку [a;b].
В общем виде определенный интеграл можно записать таким образом:
Вычислить определенный интеграл можно с помощью уравнения Ньютона-Лейбница:
Свойства определенных интегралов:
Таблица интегралов для студентов (основные формулы)
Существует несколько основных приемов решения задач с интегралами. Процесс заключается в интегрировании функции по переменной. В том случае, если интеграл обладает табличным видом, то проблем с поиском его значения не возникнет. Когда форма записи интеграла отлична от табличной, решение сводится к приведению интеграла к табличному виду.
Таблица первообразных для решения интегралов имеет следующий вид:
В первую очередь необходимо ознакомиться с основными свойствами интегралов:
С помощью данных понятий можно решать несложные интегралы. Но в большинстве случаев встречаются задачи с непростыми интегралами, для работы с которыми требуется прибегнуть к дополнительным приемам.
Правила вычисления интегралов, примеры решения
Специальные методики позволяют рассчитывать большую часть интегралов. Основными приемами для поиска решений являются:
Решать интегралы целесообразно с помощью данного алгоритма:
На первых этапах обучения следует проверять собственные решения задач на интегралы. Для этого можно дифференцировать полученное выражение и сравнить его с исходным интегралом.
Примеры решения интегралов:
Задача 1
Требуется решить интеграл:
Решение
Заметим, что по условию интеграл — неопределенный. Сначала необходимо найти первообразную. Для этого интеграл суммы можно разложить на сумму интегралов:
Таким образом, каждый из интегралов преобразован в табличный вид. Решение можно найти с помощью таблицы:
Выполним проверку решения с помощью поиска производной:
Задача 2
Требуется решить интеграл:
Решение
После преобразований получим \(\int tdx.\)
Выражение dx также требуется заменить на t. В таком случае:
Выполним подстановку значений:
Задача 3
Необходимо найти решение интеграла:
Решение
В рамках данной задачи целесообразно выделить полный квадрат:
Результат преобразований соответствует табличному виду. Можно найти первообразную:
В результате получим:
Математический анализ — достаточно сложная дисциплина. Одной из главных тем является решение интегралов. С подобными задачами часто сталкиваются учащиеся профильных вузов. Если в процессе обучения студент испытывает какие-либо трудности, правильное решение — обратиться к сервису Феникс.Хелп.
Алгебра
План урока:
Криволинейная трапеция и понятие определенного интеграла
Построим на плоскости график произвольной функции у(х), который полностью располагается выше горизонтальной оси Ох. Далее проведем две вертикальные линии, пересекающие ось Ох в некоторых точках a и b. В результате мы получим интересную фигуру, которая на рисунке показана штриховкой:
Особенностью этой фигуры является то, что одна из ее сторон (верхняя) – это не прямая линия, а какая-то произвольная кривая. Условно будем считать эту фигуру четырехугольником, ведь у нее действительно четыре угла и четыре стороны. Две из них (вертикальные красные линии), очевидно, параллельны друг другу. Две другие стороны (кривую линию и участок оси Ох) параллельными назвать никак нельзя.
Напомним, что в геометрии четырехугольник, у которого две стороны параллельны друг другу, а две другие не параллельны, называют трапецией. Поэтому полученную нами фигуру мы также назовем трапецией. Но так как одна из ее сторон кривая, то мы будем использовать термин «криволинейная трапеция», чтобы отличать ее от трапеции «настоящей».
У каждой плоской фигуры есть площадь, и криволинейная трапеция – не исключение. Но как ее подсчитать? Есть приближенный способ подсчета. Разобьем отрезок [a; b] на несколько более мелких отрезков, и построим на каждом из них прямоугольник:
Обозначим площадь первого прямоугольника как S1, площадь второго прямоугольника – как S2 и т. д. Мы строим прямоугольники таким образом, что их левая сторона в точности равна значению функции в соответствующей точке. Обозначим те точки, на которых стоят стороны прямоугольника, как х1, х2, х3 и т. д. Тогда значения функции в этих точках будут соответственно равны у(х1), у(х2) и т. д.:
Площадь каждого полученного прямоугольника подсчитать несложно – она равна произведению его высоты на ширину. Мы организовали разбиение на прямоугольники таким образом, что ширина у них одинакова. Обозначим ее как ∆х. Тогда площадь каждого отдельного прямоугольника равна
Тогда общая площадь криволинейной трапеции приближенно будет равна сумме площадей всех треугольников:
где n – это количество прямоугольников (на рисунках мы выбрали n = 10).
Ясно, что чем больше число n, тем более точное приближение мы получим. Например, если разбить трапецию уже не на 10, а на 20 прямоугольников, то получим такую картинку:
Обратите внимание, что ширина каждого прямоугольника, то есть величина ∆х, уменьшилась.
При росте числа n ошибка при оценке площади трапеции будет уменьшаться и стремится к нулю. Поэтому в предельном случае, когда n стремится к бесконечности, в формуле (1) вместо знака приближенного равенства «≈» можно поставить знак «=». При этом величина ∆х также будет стремится к нулю, то есть становится бесконечно малой. В математике для таких величин вместо символа ∆ принято использовать букву d, то есть вместо ∆х мы напишем dx. С учетом всего этого формула (1) примет вид:
В правой части стоит сумма бесконечного числа слагаемых. У нее есть специальное название – определенный интеграл. Ясно, что величина этой суммы, то есть площадь трапеции, зависят от чисел а и b (боковых границ трапеции). Поэтому обозначение интеграла выглядит так:
Обозначение очень похоже на неопределенный интеграл. Единственное отличие – это появление чисел а и b, которые определяют боковые границы трапеции. Число b называют верхним пределом интегрирования, а число a– нижним пределом интегрирования. Дадим более строгое определение понятию определенного интеграла.
Геометрический смысл определенного интеграла заключается в том, что он равен площади криволинейной трапеции, ограниченной графиком функции у(х) и вертикальными прямыми, проходящими через точки а и b.
Формула Ньютона-Лейбница
Изначально мы хотели научиться вычислять площадь криволинейной трапеции, однако пока что мы лишь придумали, как ее обозначать – через определенный интеграл. Но как вычислить значение его значение? Оказывается, определенный интеграл очень тесно связан с неопределенным интегралом, и эта связь описывается формулой Ньютона-Лейбница.
Ещё раз построим криволинейную трапецию, а ее площадь обозначим как S. Пусть ее левая граница совпадает с осью Оу, а правая будет равна некоторому значению х0. Дело в том, что нас будет интересовать зависимость площади трапеции от значения ее правой границы, то есть некоторая функция S(x). Обозначим площадь получившейся трапеции как S(x0):
Теперь сдвинем правую границу вправо на величину ∆х. В итоге получим новую трапецию, площадь которой можно записать как S(x0 + ∆x). При этом ее площадь увеличилась на некоторую величину ∆S:
Получается, что мы дали некоторое приращение аргумента ∆х, и получили приращение функции ∆S. Мы уже выполняли похожие действия в рамках предыдущих уроков, изучая понятие производной.
Итак, мы можем записать, что
Оценим величину ∆S. Если заменить соответствующую площадь прямоугольником, то его площадь окажется равной произведению ширины прямоугольника (она равна ∆x) на высоту, которая равна у(х0):
Поделим обе части равенства (2) на величину ∆х и получим:
А теперь устремим величину ∆х к нулю. В результате в равенство (2), а значит, и (3) будет становиться все более точным. В итоге мы можем написать, что
Хорошо подумайте, что мы получили. Вспомните определение производной. Оказывается, в левой части равенства (4) стоит не что иное, как производная функции S! То есть мы можем написать, что
Получается, что производная функции S на равна значению функции у(х). А это значит, что она является ее первообразной:
Здесь F(x) – первообразная функции у(х), а F(x0) – конкретное значение этой первообразной в точке х0.
Теперь рассмотрим более привычную криволинейную трапецию, у которой правой и левой границей являются числа а и b:
Как найти ее площадь? С помощью формулы (5) мы можем найти две площади:
Из рисунков очевидно, что площадь интересующей нас трапеции равна разности величин S(b) и S(a):
Эту площадь мы и обозначаем определенным интегралом. То есть можно записать, что
Таким образом, чтобы найти площадь криволинейной трапеции, необходимо проинтегрировать функцию у(х), а потом в полученную первообразную подставить числа а и b вычесть один результат из другого.
Для примера вычислим площадь криволинейной трапеции, ограниченной линией у = х 2 и вертикальными прямыми х = 1 и х = 3.
Отметим, что в обоих случаях речь идет об одной и той же первообразной, поэтому значения констант С у них одинаковы. Теперь вычитаем из F(3) величину F(1):
Константы интегрирования сократились. Для простоты решение записывают в несколько более короткой форме. Сначала сразу после определенного интеграла пишут первообразную (то есть находят неопределенный интеграл), причем без константы интегрирования
Далее ставят вертикальную черту и пишут пределы интегрирования, которые надо подставить в первообразную:
Потом ставят знак равно и подставляют в первообразную верхнее и нижнее число, после чего выполняют оставшиеся арифметические действия:
Задание. Вычислите
Задание. Найдите площадь фигуры, ограниченной полуволной синусоиды и осью Ох.
Решение. Сначала построим схематичный график у = sinx, чтобы понять, что именно нам надо вычислить:
Теперь ясно, что надо произвести вычисление определенного интеграла синуса на отрезке [0; π]:
Итак, мы теперь знаем и про определенный, и про неопределенный интеграл. Хотя они и очень похожи, между ними есть большая разница, и ее важно понимать. Определенный интеграл – это число, а именно величина площади криволинейной трапеции. Неопределенный интеграл – это функция (точнее, семейство функций), которая является первообразной для интегрируемой функции. Формула Ньютона-Лейбница как раз и показывает ту связь, которая есть между двумя этими различными понятиями.
Может ли определенный интеграл быть отрицательным числом? Кажется, что нет, ведь площадь фигур не бывает отрицательной. Но не всё так просто. Рассмотрим случай, когда график функции является не верхней, а нижней границей трапеции. Например, пусть трапеция образована функцией
Просто надо найти определенный интеграл:
Получили отрицательное значение. Дело в том, что фигура располагается под осью Ох. Из-за этого ее площадь получается со знаком минус.
Рассмотрим ещё один пример. Найдем интеграл косинуса на промежутке от 0 до 2π:
Получился ноль. Посмотрим на графике, какую же площадь мы посчитали:
Оказывается, график на отрезке дважды пересекает ось Ох. В результате получается сразу три криволинейных трапеции. Две из них расположены выше оси Ох, а потому из площади считаются со знаком «+». Третья трапеция лежит ниже оси Ох, а потому ее площадь считается со знаком «–». То, что интеграл оказался равным нулю, означает, что площадь нижней трапеции в точности равна сумме площадей двух верхних фигур, поэтому в сумме они и дали ноль.
Отметим важное свойство определенного интеграла:
Проиллюстрируем это правило графически. Каждый из этих интегралов равен площади соответствующих криволинейных трапеций:
Задачи, связанные с определенным интегралом
Определенный интеграл помогает находить и площади более сложных фигур, которые получаются при пересечении нескольких различных графиков.
Рассмотрим задачу на интеграл. Пусть требуется найти площадь фигуры, полученной при пересечении параболы
Сначала найдем точки пересечения графиков. Для этого приравняем функции:
Корнями этого квадратного уравнения являются числа 1 и 4. Именно в этих точках и пересекаются графики (это и так видно из графика). Площадь интересующей нас фигуры можно получить вычитанием из одной криволинейной трапеции другой:
Величины S1и S2 можно вычислить через определенный интеграл. Обратите внимание, что найденные нами корни являются пределами интегрирования:
Тогда искомая нами площадь составит
Ошибочно думать, что определенные интегралы нужны только для расчета площадей. С их помощью можно и решать ряд физических задач. Пусть известен закон изменения скорости тела v(t). Можно доказать, что путь, пройденный этим телом за период времени с t1по t2, будет равен интегралу
Задание. Самолет разгоняется, однако из-за сопротивления воздуха он набирает скорость не равномерно. Скорость самолета в момент времени t может быть вычислена по формуле
Определите, какое расстояние пролетит самолет в период времени между 16-ой и 25-ой секундой разгона.
Решение. Задача сводится к простому вычислению интеграла:
Ответ: 610 метров.
Этот пример показывает важную зависимость между скоростью тела и путем, который она преодолевает. Если есть график изменения скорости тела, то площадь под этим графиком равна тому пути, которое проходит тело:
Действительно, если тело двигается равномерно (то есть с постоянной скоростью), то путь, пройденный им, может быть вычислен по известной формуле
Но если построить для такого случая график v(t), то он будет выглядеть как горизонтальная прямая линия. Тогдафигура под графиком окажется прямоугольником, чья площадь равна произведению длины и ширины:
Заметим, что зависимость между путем, скоростью временем носит линейный характер, и именно поэтому здесь может быть использован неопределенный интеграл. Но ведь в физике очень много линейных зависимостей! И во всех этих случаях интегралы играют огромную роль!
Рассмотрим задачу. Есть пружина, которая изначально находится в нерастянутом состоянии. Потом человек начинает медленно и с постоянной скоростью, растягивать пружину, увеличивая ее длину на 0,5 метра. Жесткость пружины (ее коэффициент упругости) равна 100 Н/м. Какую работу совершил человек при растягивании пружины?
Из средней школы известна следующая формула для вычисления работы:
где F– сама сила, а S– путь, пройденный телом под действием этой силы. Легко заметить, что эта формула похожа на ранее рассмотренную зависимость пути от скорости и времени (они обе являются линейными). Сначала рассмотрим простой случай, когда сила остается неизменной. Тогда можно построить график F(S). Окажется, что площадь под графиком как раз равна работе, совершенной силой:
Случай с пружиной сложнее, ведь сила при растяжении пружины не остается неизменной. Чем сильнее растянута пружина, с тем большей силой ее приходится тянуть. Известен закон Гука, связывающий удлинение пружины с силой ее натяжения:
где k – коэффициент жесткости пружины, а x– ее удлинение. По смыслу задачи максимальное удлинение известно и равно 0,5 м. Можно нарисовать такой график зависимости силы натяжения пружины от ее удлинения (он будет выглядеть как прямая линия, так как эта зависимость является прямой пропорциональностью):
И в данном случае работа также будет равна площади под графиком функции, то есть ее можно посчитать с помощью определенного интеграла! В качестве пределов интегрирования надо взять крайние значения удлинения пружины (это 0 и 0,5 м), а качестве интегрируемой функции – F(t), которая равна
Существует и много других примеров приложений определенного интеграла. С его помощью можно находить объемы сложных фигур (конуса, пирамиды, тел вращения), определять центр масс тел сложной формы. Следует отметить и использование интегралов в механике при решении задач, в которых сила действует не на конкретную точку, а на площадь (задачи на распределенную нагрузку). В качестве примера можно привести расчет прочности крыши, на которой лежит слой снега.Но для их рассмотрения необходим более высокий уровень математических и физических знаний, который можно получить уже в рамках не среднего, а высшего образования.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Вычислить определенный интеграл (площадь криволинейной трапеции).
Этот математический калькулятор онлайн поможет вам вычислить определенный интеграл (площадь криволинейной трапеции). Программа для вычисления определенного интеграла (площади криволинейной трапеции) не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс интегрирования функции.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Немного теории.
Определенный интеграл.
Задачи, приводящие к понятию определенного интеграла
Задача 1 (о вычислении площади криволинейной трапеции).
В декартовой прямоугольной системе координат xOy дана фигура (см. рисунок), ограниченная осью х, прямыми х = a, х = b (a \( S_n = f(x_0)\Delta x_0 + \dots + f(x_k)\Delta x_k + \dots + f(x_
Здесь ради единообразия обозначений мы считаем, что a = х0, b = xn;
\( \Delta x_0 \) — длина отрезка [x0; x1],
\( \Delta x_1 \) — длина отрезка [x1; x2], и т.д;
при этом, как мы условились выше, \( \Delta x_0 = \dots = \Delta x_
Подведем итоги. Решения различных задач свелись к одной и той же математической модели. Многие задачи из различных областей науки и техники приводят в процессе решения к такой же модели. Значит, данную математическую модель надо специально изучить.
Понятие определенного интеграла
В курсе математического анализа доказано, что этот предел в случае непрерывной (или кусочно-непрерывной) функции существует. Его называют определенным интегралом от функции y = f(x) по отрезку [а; b] и обозначают так:
\( \int\limits_a^b f(x) dx \)
Числа a и b называют пределами интегрирования (соответственно нижним и верхним).
Вернемся к рассмотренным выше задачам. Определение площади, данное в задаче 1, теперь можно переписать следующим образом:
\( S = \int\limits_a^b f(x) dx \)
здесь S — площадь криволинейной трапеции, изображенной на рисунке выше. В этом состоит геометрический смысл определенного интеграла.
Определение перемещения s точки, движущейся по прямой со скоростью v = v(t), за промежуток времени от t = a до t = b, данное в задаче 2, можно переписать так:
\( S = \int\limits_a^b v(t) dt \)
Формула Ньютона — Лейбница
Для начала ответим на вопрос: какая связь между определенным интегралом и первообразной?
Ответ можно найти в задаче 2. С одной стороны, перемещение s точки, движущейся по прямой со скоростью v = v(t), за промежуток времени от t = а до t = b и вычисляется по формуле
\( S = \int\limits_a^b v(t) dt \)
В курсе математического анализа доказана следующая теорема.
Теорема. Если функция y = f(x) непрерывна на отрезке [а; b], то справедлива формула
\( S = \int\limits_a^b f(x) dx = F(b)-F(a) \)
где F(x) — первообразная для f(x).
Приведенную формулу обычно называют формулой Ньютона — Лейбница в честь английского физика Исаака Ньютона (1643—1727) и немецкого философа Готфрида Лейбница (1646— 1716), получивших ее независимо друг от друга и практически одновременно.
Вычисляя определенный интеграл, сначала находят первообразную, а затем осуществляют двойную подстановку.
Опираясь на формулу Ньютона — Лейбница, можно получить два свойства определенного интеграла.
Свойство 1. Интеграл от суммы функций равен сумме интегралов:
\( \int\limits_a^b (f(x) + g(x))dx = \int\limits_a^b f(x)dx + \int\limits_a^b g(x)dx \)
Свойство 2. Постоянный множитель можно вынести за знак интеграла:
\( \int\limits_a^b kf(x)dx = k \int\limits_a^b f(x)dx \)
Вычисление площадей плоских фигур с помощью определенного интеграла
Итак, площадь S фигуры, ограниченной прямыми х = а, х = b и графиками функций y = f(x), y = g(x), непрерывных на отрезке [a; b] и таких, что для любого x из отрезка [а; b] выполняется неравенство \( g(x) \leqslant f(x) \), вычисляется по формуле
\( S = \int\limits_a^b (f(x)-g(x))dx \)
Определенный интеграл. Примеры решений
Для того чтобы научиться решать определенные интегралы необходимо:
1) Уметь находить неопределенные интегралы.
2) Уметь вычислить определенный интеграл.
Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений.
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования.
Нижний предел интегрирования стандартно обозначается буквой 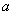
Верхний предел интегрирования стандартно обозначается буквой 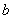
Отрезок 
Прежде чем мы перейдем к практическим примерам, небольшое «факью» по определенному интегралу.
Что такое определенный интеграл? Я бы мог вам рассказать про диаметр разбиения отрезка, предел интегральных сумм и т.д., но урок носит практический характер. Поэтому я скажу, что определенный интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число.
Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла.
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.
Как решить определенный интеграл?С помощью знакомой со школы формулы Ньютона-Лейбница:
Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию 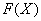
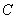

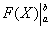
2) Подставляем значение верхнего предела в первообразную функцию: 
3) Подставляем значение нижнего предела в первообразную функцию: 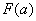
4) Рассчитываем (без ошибок!) разность 
Всегда ли существует определенный интеграл? Нет, не всегда.
Например, интеграла 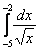



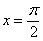

Для того чтобы определенный интеграл вообще существовал, необходимо чтобы подынтегральная функция быланепрерывнойна отрезке интегрирования.
Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования. По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?». В упрощенном варианте ситуация выглядит примерно так:
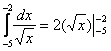
Нельзя подставлять отрицательные числа под корень!
Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен несуществующий интеграл вроде

то нужно дать ответ, что интеграла не существует и обосновать – почему.
Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будетнесобственный интеграл, коим отведена отдельная лекция.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?Может, и такая ситуация реально встречается на практике.
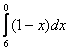
Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.
В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:
Например, в определенном интеграле перед интегрированием 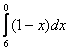

Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:
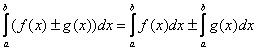
В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.
Для определенного интеграла справедлива формула интегрирования по частям:
Вычислить определенный интеграл
Решение:
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью самой популярной формулы 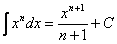
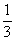
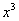
(3) Используем формулу Ньютона-Лейбница
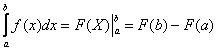
Сначала подставляем в 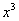
Вычислить определенный интеграл
Это пример для самостоятельно решения, решение и ответ в конце урока.
Немного усложняем задачу:
Вычислить определенный интеграл
Решение:
(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:
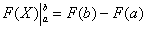
СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряю на третьем слагаемом:
– первое место в хит-параде ошибок по невнимательности, очень часто машинально пишут
(особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.
Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, я сам привык решать подобные интегралы так:
Здесь я устно использовал правила линейности, устно проинтегрировал по таблице. У меня получилась всего одна скобка с отчёркиванием пределов:
(в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию, я сначала подставил сначала 4, затем –2, опять же выполнив все действия в уме.
Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, но лично мне всё равно – обыкновенные дроби я считаю на калькуляторе.
Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту-чайнику лучше использовать первый способ, при «моём» способе решения точно где-нибудь потеряется знак.
Несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная