Как решить неравенство
Как решить неравенство
Решение линейных неравенств
Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для сравнения величин.
| Символ | Название | Тип знака |
|---|---|---|
| > | больше | строгий знак (число на границе не включается ) |
| строгий знак (число на границе не включается ) | ||
| ≥ | больше или равно | нестрогий знак (число на границе включается ) |
| ≤ | меньше или равно | нестрогий знак (число на границе включается ) |
Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство отличается от уравнения.
В отличии от уравнения в неравенстве вместо знака равно « = » используют любой знак сравнения: « > », « », « ≤ » или « ≥ ».
Линейным неравенством называют неравенство, в котором неизвестное стоит только в первой степени.
Рассмотрим пример линейного неравенства.
Как решить линейное неравенство
Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное в первой степени с коэффициентом « 1 ».
При решении линейных неравенств используют правило переноса и правило деления неравенства на число.
Правило переноса в неравенствах
Также как и в уравнениях, в неравенствах можно переносить любой член неравенства из левой части в правую и наоборот.
Вернемся к нашему неравенству и используем правило переноса.
Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить, понятие числовой оси.
Нарисуем числовую ось для неизвестного « x » и отметим на ней число « 14 ».
При нанесении числа на числовую ось соблюдаются следующие правила:
Заштрихуем на числовой оси по полученному ответу « x » все решения неравенства, то есть область слева от числа « 14 ».
Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство « x − 6 » даст верный результат.
Возьмем, например число « 12 » из заштрихованной области и подставим его вместо « x » в исходное неравенство « x − 6 ».
Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства.
Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство дают верный результат.
Решением неравенства называют множество чисел из заштрихованной области на числовой оси.
В нашем примере ответ « x » можно понимать так: любое число из заштрихованной области (то есть любое число меньшее « 14 ») будет являться решением неравенства « x − 6 ».
Правило умножения или деления неравенства на число
Рассмотрим другое неравенство.
Используем правило переноса и перенесём все числа без неизвестного, в правую часть.
Теперь нам нужно сделать так, чтобы при неизвестном « x » стоял коэффициент « 1 ». Для этого достаточно разделить и левую, и правую часть на число « 2 ».
При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.
Разделим « 2x > 16 » на « 2 ». Так как « 2 » — положительное число, знак неравенства останется прежним.
Рассмотрим другое неравенство.
Разделим неравенство на « −3 ». Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.
Решение неравенств
Еще раз повторим основные правила:
— Равносильными называются неравенства, множества решений которых совпадают.
— Если обе части неравенства умножить на отрицательное число, знак неравенства поменяется на противоположный. А если на положительное число – знак неравенства останется тем же.
— Возводить обе части неравенства в квадрат можно только если они неотрицательны.
— Извлекать корень из неравенства нельзя. Нет такого действия!
— Если в неравенстве можно сделать замену переменной – сделайте замену переменной. А потом аккуратно вернитесь к той переменной, которая была вначале.
— Если вы решаете простейшее показательное или логарифмическое неравенство – не забудьте сравнить основание степени (или логарифма) с единицей.
— Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений.
— Решение неравенства лучше всего записывать в виде цепочки равносильных переходов.
— Если вы воспользовались методом рационализации (замены множителя) – соответствующие формулы лучше доказать.
Основные правила решения неравенств. Алгебра 9 класс
Теория:
Алгебраические неравенства.
Квадратные неравенства. Рациональные неравенства высших степеней.
Дробно-рациональные неравенства.
Методы решения неравенств зависят в основном от того, к какому классу относятся функции, составляющие неравенство.
Чтобы решить неравенство можно:
Это неравенство верно при любом х, кроме х = 6.
3) x² + 4x + 15 0. Квадратный трехчлен положителен при всех х.
Многочлен высшей степени следует разложить на множители, то есть неравенство записать в виде
Данное неравенство равносильно следующей совокупности
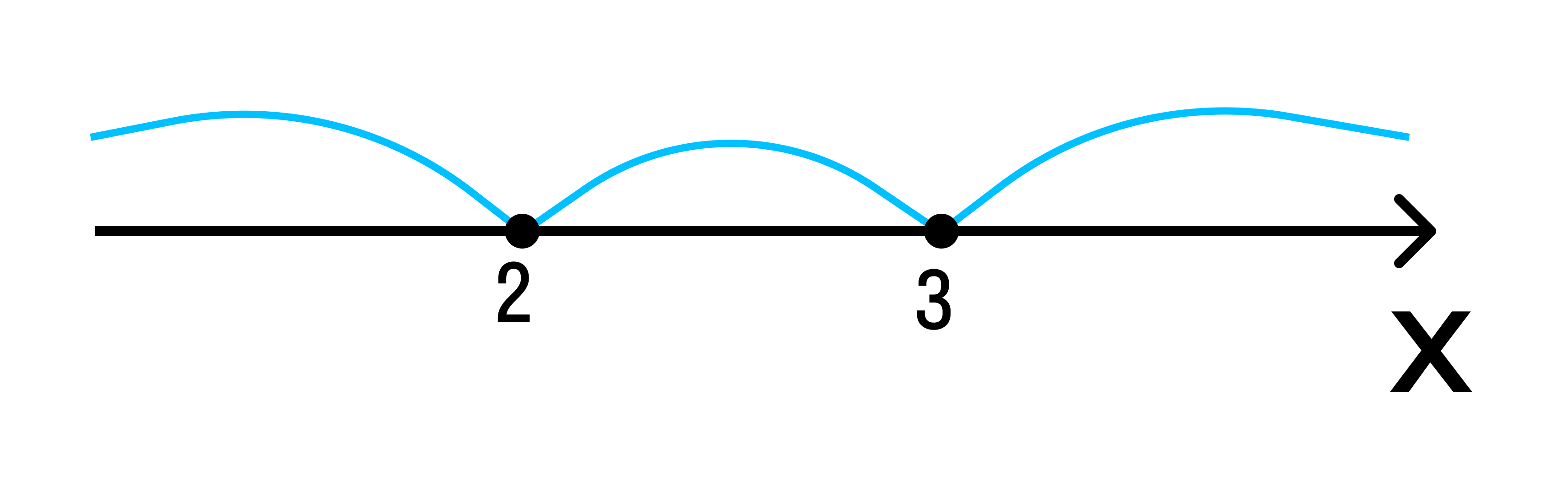
Найдем нули числителя и знаменателя. Это х = 3, х = 5, х=1. Наносим найденные точки на числовую ось и определяем знаки в каждом промежутке
Выбираем любой х(5; +), например х = 10. Тогда 0. При х = 2 (1; 3). Получаем > 0.
Наконец, при х = 0 (-; 1). Вычисляем
Метод интервалов, решение неравенств
Определение квадратного неравенства
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
где x — переменная,
Квадратное неравенство можно решить двумя способами:
Решение неравенства графическим методом
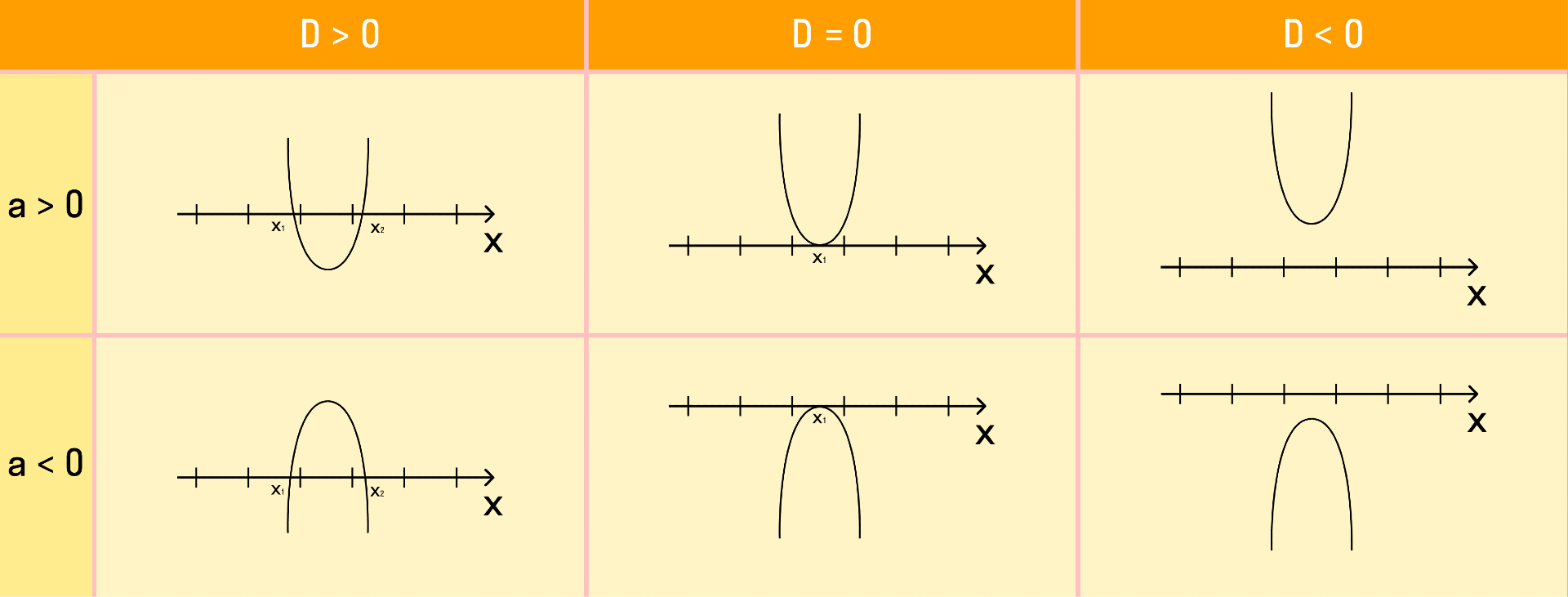
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax 2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
Если требуется найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если нужно найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.
Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:
Следовательно, искомый знак — плюс.
Можно расставить знаки быстрее, если запомнить эти факты:
Плюс или минус: как определить знаки
Можно сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, −, +,
если a 0, последовательность знаков: +, +,
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.
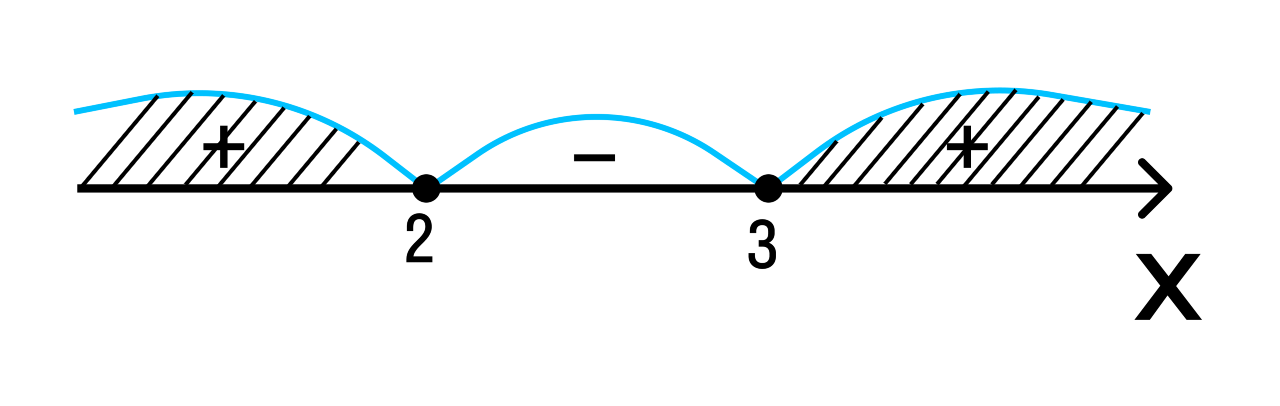
Отметим полученные значения на числовой прямой:
Расставим знаки на полученных промежутках:
Ответ: х ≤ 2, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
Решение линейных неравенств
Основные понятия
Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.
Линейные неравенства — это неравенства вида:
где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти все значения переменной, при которой неравенство верное.
Типы неравенств
Линейные неравенства: свойства и правила
Вспомним свойства числовых неравенств:
Если же а b и c > d, то а + c > b + d.
Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если а d, то а – c b, m — положительное число, то mа > mb и
Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
Если же а > b, n — отрицательное число, то nа
Обе части можно умножить или разделить на одно отрицательное число, при этом знак неравенства поменять на противоположный.
Если а 0, то аc b, где а, b > 0, то а2 > b2, и если а b, где а, b > 0, то
b» height=»45″ src=»https://lh5.googleusercontent.com/MuRDPQeqxIZvVG_mHVaktFp6nlIEEbz8zdRs1ZW8CZbZacJrS4aKzrDyhKxXpJvc35TSAgiRpqr-63sGzL9_sPU80vFhR0ZDAmSmRFZtwEldDkWRttfSGuaJJIb7xWxZDugU3xTt»>
Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.
Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.
Свойства выше помогут нам использовать следующие правила.
Правила линейных неравенств
Решение линейных неравенств
Линейные неравенства с одной переменной x выглядят так:
где a и b — действительные числа. А на месте x может быть обычное число.
Равносильные преобразования
Рассмотрим пример: 0 * x + 5 > 0.
Как решаем:
Метод интервалов
Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.
Метод интервалов заключается в следующем:
Если a ≠ 0, тогда решением будет единственный корень — х₀;
Для этого найдем значения функции в точках на промежутке;
Как решаем:
В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,
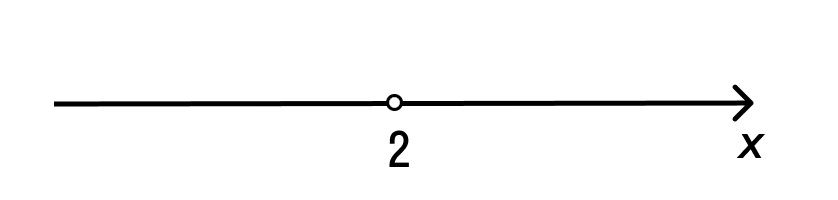
Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.
Определим знаки на промежутках.
Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.
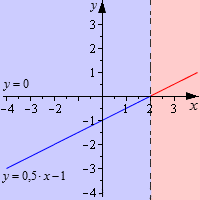
Графический способ
Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.
Алгоритм решения y = ax + b графическим способом
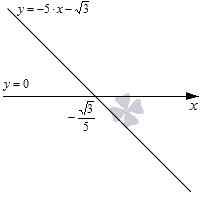
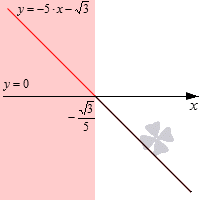
Рассмотрим пример: −5 * x − √3 > 0.
Как решаем
Ответ: (−∞, −√3 : 5) или x
Линейные неравенства, примеры, решения
После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.
Что такое линейное неравенство?
В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Их различия заключаются в:
Считается, что неравенства a · x + b > 0 и a · x > c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0 · x + 5 > 0 приведет к тому, что его необходимо будет решить, причем случай а = 0 не подойдет.
Как решить линейное неравенство
Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.
Используя равносильные преобразования
Рассмотрим применение данного алгоритма на решении примеров.
Весь выше прописанный алгоритм записывается так:
Весь алгоритм запишем в краткой форме:
Ответ: решений нет.
Ответ: неравенство 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет решения.
Методом интервалов
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов – это:
Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.
Графическим способом
Алгоритм решения линейных неравенств графическим способом.
Построение графика функции y = a · x + b производится:
Неравенства, сводящиеся к линейным
Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
7 · x − 7 + 3 ≤ 4 · x − 2 + x 7 · x − 4 ≤ 5 · x − 2 7 · x − 4 − 5 · x + 2 ≤ 0 2 · x − 2 ≤ 0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
Ответ: нет решений.
Общие сведения о неравенствах
Данный материал может показаться сложным для понимания. Рекомендуется изучать его маленькими частями.
Определения и свойства
Неравенством мы будем называть два числовых или буквенных выражения, соединенных знаками >, 5 > 3
Данное неравенство говорит о том, что число 5 больше, чем число 3. Острый угол знака неравенства должен быть направлен в сторону меньшего числа. Это неравенство является верным, поскольку 5 больше, чем 3.
Если на левую чашу весов положить арбуз массой 5 кг, а на правую — арбуз массой 3 кг, то левая чаша перевесит правую, и экран весов покажет, что левая чаша тяжелее правой:
Числа, которые располагаются в левой и правой части неравенства, будем называть членами этого неравенства. Например, в неравенстве 5 > 3 членами являются числа 5 и 3.
Свойство 1.
Если к левой и правой части неравенства 5 > 3 прибавить или вычесть одно и то же число, то знак неравенства не изменится.
Например, прибавим к обеим частям неравенства число 4. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем вычесть из обеих частей неравенства 5 > 3 какое-нибудь число, скажем число 2
Видим, что левая часть по-прежнему больше правой.
Из данного свойства следует, что любой член неравенства можно перенести из одной части в другую часть, изменив знак этого члена. Знак неравенства при этом не изменится.
Видим, что левая часть по-прежнему больше правой.
Свойство 2.
Если обе части неравенства умножить или разделить на одно и то же положительное число, то знак неравенства не изменится.
Например, умножим обе части неравенства 5 > 3 на какое-нибудь положительное число, скажем на число 2. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь число. Разделим их на 2
Видим, что левая часть по-прежнему больше правой.
Свойство 3.
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь отрицательное число. Давайте разделим их на −1
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Само по себе неравенство можно понимать, как некоторое условие. Если условие выполняется, то неравенство является верным. И наоборот, если условие не выполняется, то неравенство не верно.
Неравенство 8 не является верным, поскольку не выполняется условие «8 меньше, чем 6».
Другим способом определения верности неравенства является составление разности из левой и правой части данного неравенства. Если разность положительна, то левая часть больше правой части. И наоборот, если разность отрицательна, то левая часть меньше правой части. Более точно это правило выглядит следующим образом:
Число a больше числа b, если разность a − b положительна. Число a меньше числа b, если разность a − b отрицательна.
Например, мы выяснили, что неравенство 7 > 3 является верным, поскольку число 7 больше, чем число 3. Докажем это с помощью правила, приведённого выше.
Строгие и нестрогие неравенства
Запись 2 ≤ 5 является неполной. Полная запись этого неравенства выглядит следующим образом:
Пример 2. Неравенство 2 ≤ 2 является верным, поскольку выполняется одно из его условий, а именно 2 = 2.
Двойное неравенство
Чтобы правильно записать двойное неравенство, сначала записывают член находящийся в середине, затем член находящийся слева, затем член находящийся справа.
Например, запишем, что число 6 больше, чем число 4, и меньше, чем число 9.
Сначала записываем 6
Слева записываем, что это число больше, чем число 4
Справа записываем, что число 6 меньше, чем число 9
Неравенство с переменной
Неравенство, как и равенство может содержать переменную.
Решить неравенство означает найти такие значения переменной x, при которых данное неравенство становится верным.
Значение переменной, при котором неравенство становится верным, называется решением неравенства.
Неравенство x > 2 становится верным при x = 3, x = 4, x = 5, x = 6 и так далее до бесконечности. Видим, что это неравенство имеет не одно решение, а множество решений.
Другими словами, решением неравенства x > 2 является множество всех чисел, бóльших 2. При этих числах неравенство будет верным. Примеры:
Как решать неравенства
Процесс решения неравенств во многом схож с процессом решения уравнений. При решении неравенств мы будем применять свойства, которые изучили вначале данного урока, такие как: перенос слагаемых из одной части неравенства в другую часть, меняя знак; умножение (или деление) обеих частей неравенства на одно и то же число.
Эти свойства позволяют получить неравенство, которое равносильно исходному. Равносильными называют неравенства, решения которых совпадают.
А при решении неравенств мы будем заменять исходное неравенство на равносильное ему неравенство до тех пор, пока в левой части не останется переменная этого неравенства, а в правой части его граница.
Пример 1. Решить неравенство 2x > 6
Вначале данного урока было сказано, что если обе части неравенства разделить на какое-нибудь положительное число, то знак неравенства не изменится. Если применить это свойство к неравенству, содержащему переменную, то получится неравенство равносильное исходному.
В нашем случае, если мы разделим обе части неравенства 2x > 6 на какое-нибудь положительное число, то получится неравенство, которое равносильно исходному неравенству 2x > 6.
Итак, разделим обе части неравенства на 2.
Теперь можно сделать вывод, что решениями неравенства x > 3 являются все числа, которые больше 3. Это числа 4, 5, 6, 7 и так далее до бесконечности. При этих значениях неравенство x > 3 будет верным.
Отметим, что неравенство x > 3 является строгим. « Переменная x строго больше трёх».
Видим, что в обоих случаях получается верное неравенство.
После того, как неравенство решено, ответ нужно записать в виде так называемого числового промежутка следующим образом:
Учитывая, что понятие числового промежутка очень важно, остановимся на нём подробнее.
Числовые промежутки
Числовым промежутком называют множество чисел на координатной прямой, которое может быть описано с помощью неравенства.
Допустим, мы хотим изобразить на координатной прямой множество чисел от 2 до 8. Для этого сначала на координатной прямой отмечаем точки с координатами 2 и 8, а затем выделяем штрихами ту область, которая располагается между координатами 2 и 8. Эти штрихи будут играть роль чисел, располагающихся между числами 2 и 8
Числа 2 и 8 назовём границами числового промежутка. Рисуя числовой промежуток, точки для его границ изображают не в виде точек как таковых, а в виде кружков, которые можно разглядеть.
Границы могут принадлежать числовому промежутку либо не принадлежать ему.
Если границы не принадлежат числовому промежутку, то они изображаются на координатной прямой в виде пустых кружков.
Если границы принадлежат числовому промежутку, то кружки необходимо закрасить.
На нашем рисунке кружки были оставлены пустыми. Это означало, что границы 2 и 8 не принадлежат числовому промежутку. Значит в наш числовой промежуток будут входить все числа от 2 до 8, кроме чисел 2 и 8.
Если мы хотим включить границы 2 и 8 в числовой промежуток, то кружки необходимо закрасить:
В данном случае в числовой промежуток будут входить все числа от 2 до 8, включая числа 2 и 8.
На письме числовой промежуток обозначается указанием его границ с помощью круглых или квадратных скобок.
Если границы не принадлежат числовому промежутку, то границы обрамляются круглыми скобками.
Если границы принадлежат числовому промежутку, то границы обрамляются квадратными скобками.
На рисунке представлено два числовых промежутка от 2 до 8 с соответствующими обозначениями:
На первом рисунке числовой промежуток обозначен с помощью круглых скобок, поскольку границы 2 и 8 не принадлежат этому числовому промежутку.
На втором рисунке числовой промежуток обозначен с помощью квадратных скобок, поскольку границы 2 и 8 принадлежат этому числовому промежутку.
С помощью числовых промежутков можно записывать ответы к неравенствам. Например, ответ к двойному неравенству 2 ≤ x ≤ 8 записывается так:
То есть сначала записывают переменную, входящую в неравенство, затем с помощью знака принадлежности ∈ указывают к какому числовому промежутку принадлежат значения этой переменной. В данном случае выражение x ∈ [ 2 ; 8 ] указывает на то, что переменная x, входящая в неравенство 2 ≤ x ≤ 8, принимает все значения в промежутке от 2 до 8 включительно. При этих значениях неравенство будет верным.
Множество решений неравенства 2 ≤ x ≤ 8 также можно изобразить с помощью координатной прямой:
В некоторых источниках границы, которые не принадлежат числовому промежутку, называют открытыми.
А в случае, когда границы принадлежат числовому промежутку, их называют закрытыми (или замкнутыми), поскольку такие границы закрывают (замыкают) собой числовой промежуток. Закрашенный кружок на координатной прямой также говорит о закрытости границ.
Существуют разновидности числовых промежутков. Рассмотрим каждый из них.
Числовой луч
Изобразим числовой луч, заданный неравенством x ≥ 3, на координатной прямой. Для этого отметим на ней точку с координатой 3, а всю оставшуюся справа от неё область выделим штрихами. Выделяется именно правая часть, поскольку решениями неравенства x ≥ 3 являются числа, бóльшие 3. А бóльшие числа на координатной прямой располагаются правее
Точка 3, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≥ 3 принадлежит множеству его решений.
На письме числовой луч, заданный неравенством x ≥ a, обозначается следующим образом:
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница числового луча принадлежит ему, а другая нет, поскольку бесконечность сама по себе границ не имеет и подразумевается, что по ту сторону нет числа, замыкающего этот числовой луч.
Учитывая то, что одна из границ числового луча закрыта, данный промежуток часто называют закрытым числовым лучом.
Запишем ответ к неравенству x ≥ 3 с помощью обозначения числового луча. У нас переменная a равна 3
Точка 2, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≤ 2 принадлежит множеству его решений.
Запишем ответ к неравенству x ≤ 2 с помощью обозначения числового луча:
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x ≤ 2. Граница 2 принадлежит множеству решений, поскольку неравенство x ≤ 2 является нестрогим.
Открытый числовой луч
Открытый числовой луч во многом похож на закрытый числовой луч. Различие в том, что граница a не принадлежит промежутку, как и граница неравенства x > a не принадлежит множеству его решений.
На координатной прямой граница открытого числового луча, заданного неравенством x > 3, будет изображаться в виде пустого кружка. Вся область, находящаяся справа, будет выделена штрихами:
Круглые скобки указывают на то, что границы открытого числового луча не принадлежат ему.
Запишем ответ к неравенству x > 3 с помощью обозначения открытого числового луча:
На письме открытый числовой луч, заданный неравенством x , обозначается следующим образом:
Запишем ответ к неравенству x с помощью обозначения открытого числового луча:
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x Граница 2 не принадлежит множеству решений, поскольку неравенство x является строгим.
Отрезок
Изобразим отрезок, заданный двойным неравенством 2 ≤ x ≤ 8 на координатной прямой. Для этого отметим на ней точки с координатами 2 и 8, а располагающуюся между ними область выделим штрихами:
На письме отрезок, заданный неравенством a ≤ x ≤ b обозначается следующим образом:
Квадратные скобки с обеих сторон указывают на то, что границы отрезка принадлежат ему. Запишем ответ к неравенству 2 ≤ x ≤ 8 с помощью этого обозначения:
Интервал
Изобразим интервал на координатной прямой:
На письме интервал, заданный неравенством a обозначается следующим образом:
Круглые скобки с обеих сторон указывают на то, что границы интервала не принадлежат ему. Запишем ответ к неравенству 2 с помощью этого обозначения:
Полуинтервал
Одна из границ полуинтервала принадлежит ему. Отсюда и название этого числового промежутка.
В ситуации с полуинтервалом a ≤ x ему (полуинтервалу) принадлежит левая граница.
А в ситуации с полуинтервалом a ему принадлежит правая граница.
Изобразим полуинтервал 2 ≤ x на координатной прямой:
Точка 2, являющаяся левой границей полуинтервала, изображена в виде закрашенного кружка, поскольку левая граница неравенства 2 ≤ x принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде пустого кружка, поскольку правая граница неравенства 2 ≤ x не принадлежит множеству его решений.
На письме полуинтервал, заданный неравенством a ≤ x обозначается следующим образом:
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница полуинтервала принадлежит ему, а другая нет. Запишем ответ к неравенству 2 ≤ x с помощью этого обозначения:
Изобразим полуинтервал 2 на координатной прямой:
Точка 2, являющаяся левой границей полуинтервала, изображена в виде пустого кружка, поскольку левая граница неравенства 2 не принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде закрашенного кружка, поскольку правая граница неравенства 2 принадлежит множеству его решений.
Изображение числовых промежутков на координатной прямой
Числовой промежуток может быть задан с помощью неравенства или с помощью обозначения (круглых или квадратных скобок). В обоих случаях нужно суметь изобразить этот числовой промежуток на координатной прямой. Рассмотрим несколько примеров.
Пример 1. Изобразить числовой промежуток, заданный неравенством x > 5
Вспоминаем, что неравенством вида x > a задаётся открытый числовой луч. В данном случае переменная a равна 5. Неравенство x > 5 строгое, поэтому граница 5 будет изображаться в виде пустого кружкá. Нас интересуют все значения x, которые больше 5, поэтому вся область справа будет выделена штрихами:
Пример 2. Изобразить числовой промежуток (5; +∞) на координатной прямой
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью неравенства, а с помощью обозначения числового промежутка.
Граница 5 обрамлена круглой скобкой, значит она не принадлежит промежутку. Соответственно, кружок остаётся пустым.
Символ +∞ указывает, что нас интересуют все числа, которые больше 5. Соответственно, вся область справа от границы 5 выделяется штрихами:
Пример 3. Изобразить числовой промежуток (−5; 1) на координатной прямой.
Круглыми скобками с обеих сторон обозначаются интервалы. Границы интервала не принадлежат ему, поэтому границы −5 и 1 будут изображаться на координатной прямой в виде пустых кружков. Вся область между ними будет выделена штрихами:
Пример 4. Изобразить числовой промежуток, заданный неравенством −5
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью обозначения промежутка, а с помощью двойного неравенства.
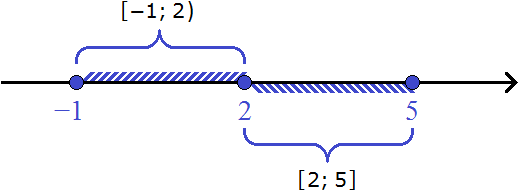
Пример 5. Изобразить на координатной прямой числовые промежутки [−1; 2) и [2; 5]
В этот раз изобразим на координатной прямой сразу два промежутка. Промежуток [−1; 2) является полуинтервалом, промежуток [2; 5] — отрезком.
У полуинтервала [−1; 2) левая граница принадлежит ему, а правая нет.
А у отрезка [2; 5] обе границы принадлежат ему.
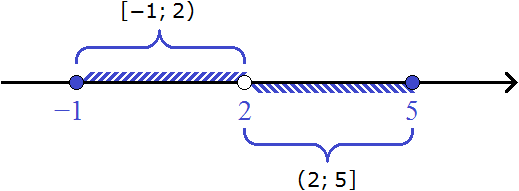
Пример 6. Изобразить на координатной прямой числовые промежутки [-1; 2) и (2; 5]
Квадратной скобкой с одной стороны и круглой с другой обозначаются полуинтервалы. Одна из границ полуинтервала принадлежат ему, а другая нет.
В случае с полуинтервалом [-1; 2) левая граница будет принадлежать ему, а правая нет. Значит левая граница будет изображаться в виде закрашенного кружка. Правая же граница будет изображаться в виде пустого кружка.
А в случае с полуинтервалом (2; 5] ему будет принадлежать только правая граница, а левая нет. Значит левая граница будет изображаться в виде пустого кружка. Правая же граница будет изображаться в виде закрашенного кружка.
Изобразим промежуток [-1; 2) на верхней области координатной прямой, а промежуток (2; 5] — на нижней:
Примеры решения неравенств
Неравенство, которое путём тождественных преобразований можно привести к виду ax > b (или к виду ax ), будем называть линейным неравенством с одной переменной.
Неравенство 2x > 4 можно сделать ещё проще. Если мы разделим обе его части на 2, то получим неравенство x > 2
Отталкиваясь от этих сведений, попробуем решить несколько простых неравенств. В ходе решения мы будем выполнять элементарные тождественные преобразования с целью получить неравенство вида ax > b
Пример 1. Решить неравенство x − 7
Прибавим к обеим частям неравенства число 7
Запишем ответ с помощью числового промежутка. В данном случае ответом будет открытый числовой луч (вспоминаем, что числовой луч задаётся неравенством x и обозначается как ( −∞ ; a)
На координатной прямой граница 7 будет изображаться в виде пустого кружка, а вся область, находящаяся слева от границы, будет выделена штрихами:
Получилось верное числовое неравенство, значит и решение верное. Возьмём ещё какое-нибудь число, например, число 4
Получилось верное числовое неравенство. Значит решение верное.
Пример 2. Решить неравенство −4x
Разделим обе части неравенства на −4. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Изобразим множество решений неравенства x > 4 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 3. Решить неравенство 3y + 1 > 1 + 6y
Перенесём 6y из правой части в левую часть, изменив знак. А 1 из левой части перенесем в правую часть, опять же изменив знак:
Приведём подобные слагаемые:
Разделим обе части на −3. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Решениями неравенства y являются все числа, меньшие нуля. Изобразим множество решений неравенства y на координатной прямой и запишем ответ в виде числового промежутка:
Пример 4. Решить неравенство 5(x − 1) + 7 ≤ 1 − 3(x + 2)
Раскроем скобки в обеих частях неравенства:
Перенесем −3x из правой части в левую часть, изменив знак. Члены −5 и 7 из левой части перенесем в правую часть, опять же изменив знаки:
Приведем подобные слагаемые:
Разделим обе части получившегося неравенства на 8
Решениями неравенства 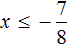
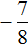
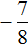
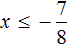
Изобразим множество решений неравенства 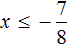
Пример 5. Решить неравенство
Умножим обе части неравенства на 2. Это позволит избавиться от дроби в левой части:
Теперь перенесем 5 из левой части в правую часть, изменив знак:
Изобразим множество решений неравенства 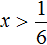
Пример 6. Решить неравенство
Умножим обе части на 6
Решениями неравенства x являются все числа, которые меньше 6. Граница 6 не принадлежит множеству решений, поскольку неравенство является x строгим.
Изобразим множество решений неравенства x на координатной прямой и запишем ответ в виде числового промежутка:
Пример 7. Решить неравенство
Умножим обе части неравенства на 10
В получившемся неравенстве раскроем скобки в левой части:
Перенесем члены без x в правую часть
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 10
Решениями неравенства x ≤ 3,5 являются все числа, которые меньше 3,5. Граница 3,5 принадлежит множеству решений, поскольку неравенство является x ≤ 3,5 нестрогим.
Изобразим множество решений неравенства x ≤ 3,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 8. Решить неравенство 4
Чтобы решить такое неравенство, нужно переменную x освободить от коэффициента 4. Тогда мы сможем сказать в каком промежутке находится решение данного неравенства.
Чтобы освободить переменную x от коэффициента, можно разделить член 4x на 4. Но правило в неравенствах таково, что если мы делим член неравенства на какое-нибудь число, то тоже самое надо сделать и с остальными членами, входящими в данное неравенство. В нашем случае на 4 нужно разделить все три члена неравенства 4
Решениями неравенства 1 являются все числа, которые больше 1 и меньше 5. Границы 1 и 5 не принадлежат множеству решений, поскольку неравенство 1 является строгим.
Изобразим множество решений неравенства 1 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 9. Решить неравенство −1 ≤ −2x ≤ 0
Разделим все члены неравенства на −2
Решениями неравенства 0 ≤ x ≤ 0,5 являются все числа, которые больше 0 и меньше 0,5. Границы 0 и 0,5 принадлежат множеству решений, поскольку неравенство 0 ≤ x ≤ 0,5 является нестрогим.
Изобразим множество решений неравенства 0 ≤ x ≤ 0,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 10. Решить неравенство
Умножим обе неравенства на 12
Раскроем скобки в получившемся неравенстве и приведем подобные слагаемые:
Разделим обе части получившегося неравенства на 2
Решениями неравенства x ≤ −0,5 являются все числа, которые меньше −0,5. Граница −0,5 принадлежит множеству решений, поскольку неравенство x ≤ −0,5 является нестрогим.
Изобразим множество решений неравенства x ≤ −0,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 11. Решить неравенство
Умножим все части неравенства на 3
Теперь из каждой части получившегося неравенства вычтем 6
Каждую часть получившегося неравенства разделим на −1. Не забываем, что при делении всех частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Решениями неравенства 3 ≤ a ≤ 9 являются все числа, которые больше 3 и меньше 9. Границы 3 и 9 принадлежат множеству решений, поскольку неравенство 3 ≤ a ≤ 9 является нестрогим.
Изобразим множество решений неравенства 3 ≤ a ≤ 9 на координатной прямой и запишем ответ в виде числового промежутка:
Когда решений нет
Для наилучшего понимания, перепишем приведение подобных слагаемых в левой части следующим образом:
Пример 2. Решить неравенство
Умножим обе части неравенства на 3
В получившемся неравенстве перенесем член 12x из правой части в левую часть, изменив знак. Затем приведём подобные слагаемые:
Правая часть получившегося неравенства при любом x будет равна нулю. А ноль не меньше, чем −8. Значит неравенство 0x не имеет решений.
Ответ: решений нет.
Когда решений бесконечно много
Пример 1. Решить неравенство 5(3x − 9)
Раскроем скобки в правой части неравенства:
Перенесём 15x из правой части в левую часть, изменив знак:
Приведем подобные слагаемые в левой части:
А если приведённое равносильное неравенство 0x имеет бесчисленное множество решений, то и исходное неравенство 5(3x − 9) имеет те же решения.
Ответ можно записать в виде числового промежутка:
В этом выражении говорится, что решениями неравенства 5(3x − 9) являются все числа от минус бесконечности до плюс бесконечности.
Пример 2. Решить неравенство: 31(2x + 1) − 12x > 50x
Раскроем скобки в левой части неравенства:
Перенесём 50x из правой части в левую часть, изменив знак. А член 31 из левой части перенесём в правую часть, опять же изменив знак:
Приведём подобные слагаемые:
А если приведённое равносильное неравенство 0x > −31 имеет бесчисленное множество решений, то и исходное неравенство 31(2x + 1) − 12x > 50x имеет те же решения.
Запишем ответ в виде числового промежутка:
Задания для самостоятельного решения
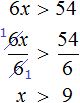

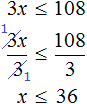

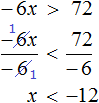

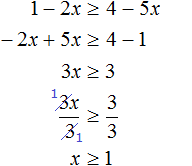

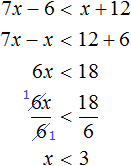

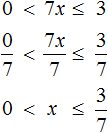

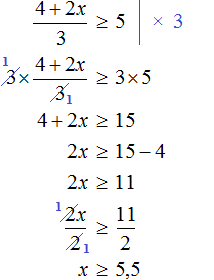

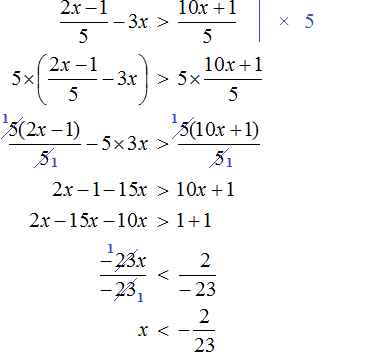

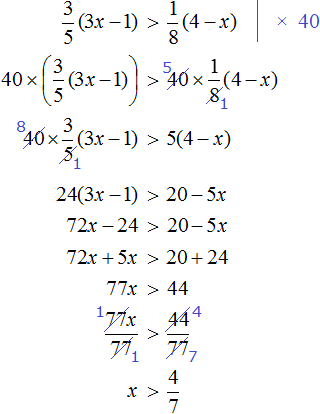

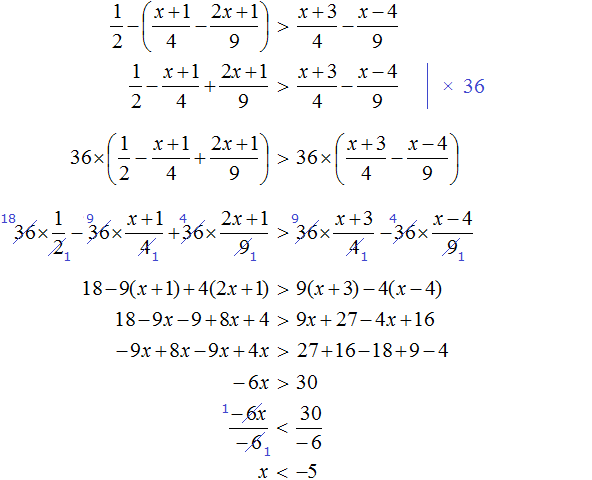

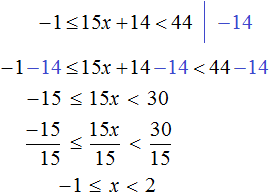


Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Неравенства. Виды неравенств
Неравенства – выражения вида \(a>b\), \(a 5\).
Виды неравенств:
Переменная только в первой степени
Есть переменная во второй степени (квадрате), но нет старших степеней (третьей, четвертой и т.д.)
Что такое решение неравенства?
Если в неравенство вместо переменной подставить какое-нибудь число, то оно превратится в числовое.
Например, если мы в линейное неравенство \(x+6>10\), подставим вместо икса число \(7\) –получим верное числовое неравенство: \(13>10\). А если подставим \(2\), будет неверное числовое неравенство \(8>10\). То есть \(7\) – это решение исходного неравенства, а \(2\) – нет.
Однако, неравенство \(x+6>10\) имеет и другие решения. Действительно, мы получим верные числовые неравенства при подстановке и \(5\), и \(12\), и \(138\). И как же нам найти все возможные решения? Для этого используют равносильные преобразования неравенств . Для нашего случая имеем:
Когда в неравенстве меняется знак?
В неравенствах есть одна большая ловушка, в которую очень «любят» попадаться ученики:
При умножении (или делении) неравенства на отрицательное число, знак сравнения меняется на противоположный («больше» на «меньше», «больше или равно» на «меньше или равно» и так далее)
Почему так происходит? Чтобы это понять, давайте посмотрим преобразования числового неравенства \(3>1\). Оно верное, тройка действительно больше единицы. Сначала попробуем умножить его на любое положительное число, например, двойку:
Как видим, после умножения неравенство осталось верным. И на какое бы положительное число мы не умножали – всегда будем получать верное неравенство. А теперь попробуем умножить на отрицательное число, например, минус тройку:
Запишем ответ в виде интервала
Неравенства и ОДЗ
Как решать неравенства — практикум ОГЭ (ГИА)
Несмотря на то, что решение неравенств очень напоминает решение уравнений, все-таки неравенства вызывают у школьников больше затруднений.
Ученики часто спрашивают как решать неравенства те или иные, просят оценить решение неравенства, полученное у доски в школе или помочь в решении домашнего задания с неравенством. В основном они связаны не с решением неравенства как такового, а с проблемой записи решения и с проблемой знака неравенства, которое в определенные моменты заменяется на противоположный.
Решение неравенств — это материал, который помогает выявить у экзаменуемого сразу несколько умений и навыков: умение решать уравнения, работать со знаком неравенства, оценить полученное решение с точки зрения постановки неравенства. Поэтому неравенства включены в ОГЭ (ГИА).
Как решать простейшие неравенства из ОГЭ (ГИА)
Итак, первое неравенство:
Как решать нестрогое неравенство
Нестрогим неравенством называется неравенство, у которого вместо строгого знака «больше» или «меньше», стоит знак «больше или равно» или «меньше или равно». Например, давайте решим нестрогое неравенство. Возьмем простое неравенство, чтобы вы поняли суть вопроса.
Решаем аналогично — только сначала упростим правую часть нашего неравенства. Переносим неизвестные в левую часть неравенства, а известные (числа) в правую часть неравенства:
Упрощаем правую часть:
Ответ: 
Обратите внимание на запись ответа. Так как у нас неравенство нестрогое, то число 2 будет входить в решение этого неравенства, поэтому мы его включаем в ответ, отмечая квадратной скобкой.
Вот так:
Решение неравенств из сборника ОГЭ по математике ФИПИ
Неравенство 1
Укажите решение неравенства
Решение:
Перенесем неизвестные в левую часть неравенства, а известные — в правую часть неравенства:

искомый интервал: 
Ответ 2.
Неравенство 2
Укажите множество решений неравенства:
Как обычно, переносим неизвестные влево от знака неравенства, а известные величины — вправо:
Обратите внимание — здесь мы делим отрицательное число. Но делим то мы его на положительное число 6. Поэтому знак неравенства остается прежним!
Нам подходит вариант решения 4.
Неравенство 3
Укажите решение неравенства
Решение:
Подходит вариант решения 2.
Ответ: 2
Неравенство 4
Укажите множество решений неравенства
Решение:
Итак, решение неравенство иллюстрируется графиком 3.
Ответ: 3.
Теперь вы знаете, как решать неравенства, которые даны в части «Алгебра» ОГЭ (ГИА).
Решение неравенств
Определение и формулы неравенств
Знаки > называются знаками строгого неравенства, а знаки 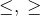
Если в неравенство входят только числовые величины, то такое неравенство называется числовым неравенством.
Решить неравенство — это значит найти множество всех его решений
Неравенства называют равносильными, если они имеют одно и тоже множество решений.
Основные правила, применяемые при решении неравенств
Если требуется все общие решения двух или нескольких неравенств, то решают систему неравенств. Как и систему уравнений, систему неравенств записывают с помощью фигурной скобки. Решение системы неравенств есть пересечение решений всех входящих в нее неравенств.
Одним из основных методов решения неравенств является метод интервалов.
Примеры решения неравенств
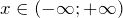
Решим каждую систему неравенств отдельно: 2. Объединим полученные решения и запишем решение исходного неравенства Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства: ≥ больше или равно, ≤ меньше или равно, то получится неравенство. Линейные неравенства – это неравенства вида: a x b a x ≤ b a x > b a x ≥ b Примеры линейных неравенств: 3 x 5 x − 2 ≥ 0 7 − 5 x 1 x ≤ 0 x c x ≤ c x > c x ≥ c Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ. Смысл выколотой точки в том, что сама точка в ответ не входит. Смысл жирной точки в том, что сама точка входит в ответ.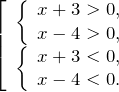
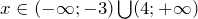
Линейные неравенства
Знаки неравенств
Линейные неравенства
Таблица числовых промежутков









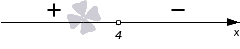
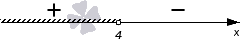
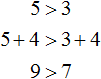
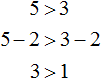
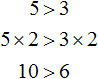
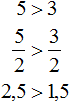
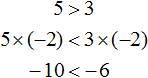
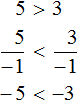
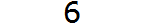
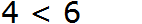
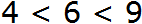
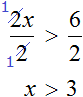
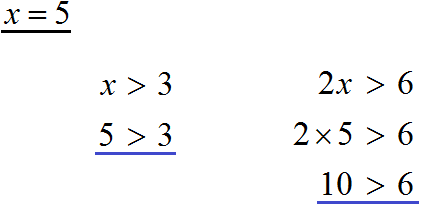
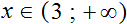


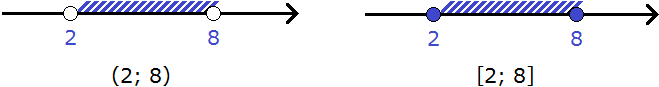











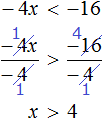

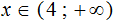
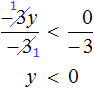

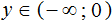
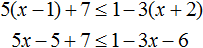
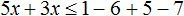
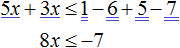
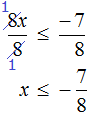

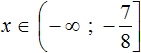
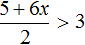
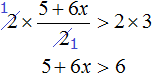
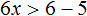
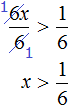

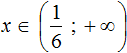
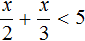
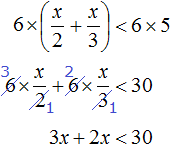
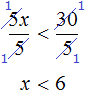

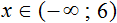
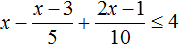
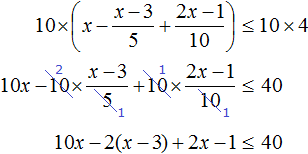
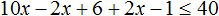
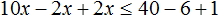
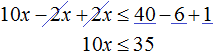
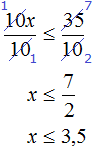

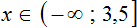
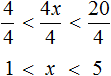

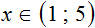
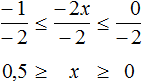

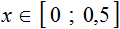
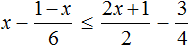
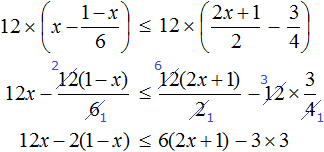
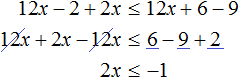
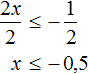

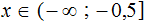
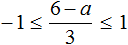
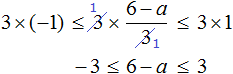
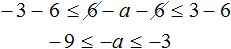
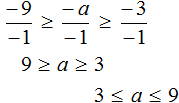

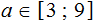
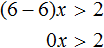
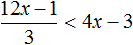
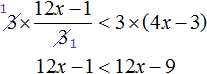
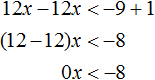
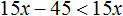
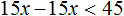
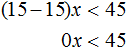
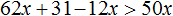
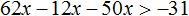
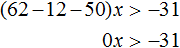
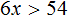
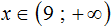
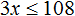
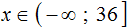
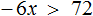
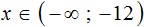
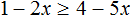
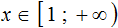
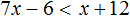
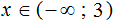
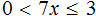
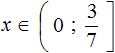
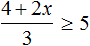
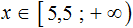
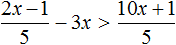
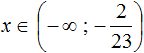
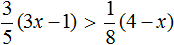
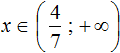
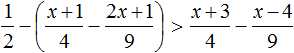
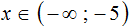
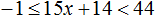
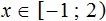
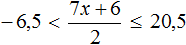
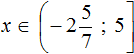

























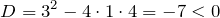






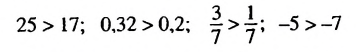
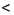 10:
10: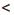 », «=» и значением разности левой и правой частей соответствующего неравенства (равенства). Эту зависимость выражает определение.
», «=» и значением разности левой и правой частей соответствующего неравенства (равенства). Эту зависимость выражает определение.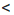 b или а = b.
b или а = b.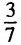 и
и 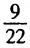 . Для этого найдем их разность:
. Для этого найдем их разность: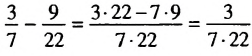

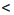 » или «>», называют строгими неравенствами, а неравенства, образованные при помощи знаков «≤» или «≥», называют нестрогими.
» или «>», называют строгими неравенствами, а неравенства, образованные при помощи знаков «≤» или «≥», называют нестрогими.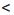 8; 1,2 ≥ -1 — верные неравенства, 21 > 30 — неверное неравенство.
8; 1,2 ≥ -1 — верные неравенства, 21 > 30 — неверное неравенство.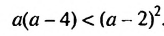
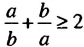 , если
, если 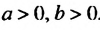 .
.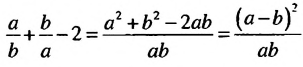
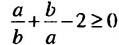 . Следовательно, неравенство
. Следовательно, неравенство 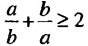 справедливо при любых положительных числах а и b.
справедливо при любых положительных числах а и b.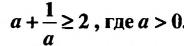
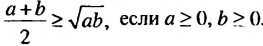
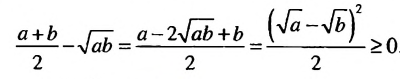
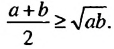
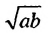 называют их средним геометрическим (или средним пропорциональным). Неравенство
называют их средним геометрическим (или средним пропорциональным). Неравенство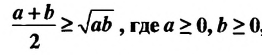
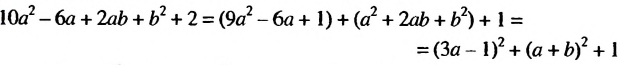
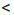 а.
а.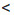 b и b
b и b 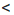 с, то а
с, то а 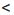 с.
с. Рис.3
Рис.3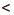 b. Докажем, что ас
b. Докажем, что ас 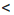 bc, если с — положительное число, и ас > bc. если с — отрицательное число. Рассмотрим разность:
bc, если с — положительное число, и ас > bc. если с — отрицательное число. Рассмотрим разность: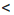 b, то
b, то 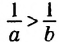 •
•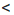 b на положительное число ab. Получим:
b на положительное число ab. Получим: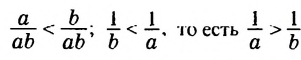
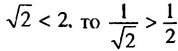 .
.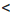 b
b 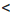 с можно записать в виде двух неравенств: а
с можно записать в виде двух неравенств: а 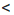 b и b
b и b 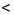 с. Если а
с. Если а 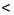 b и b
b и b 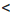 с, то для любого числа m справедливы неравенства: а + m
с, то для любого числа m справедливы неравенства: а + m 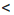 b + m и b + m
b + m и b + m 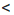 с + m, откуда а + m
с + m, откуда а + m 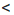 b + m
b + m 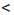 с + m.
с + m.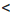 x
x 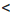 3. Оцените значение выражения:
3. Оцените значение выражения: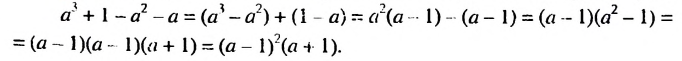
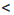 b и с
b и с 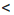 d. Нужно доказать, что а + с
d. Нужно доказать, что а + с 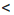 b + d. Чтобы получить сумму а + с, прибавим к обеим частям первого неравенства число с, а чтобы получить сумму b + d, прибавим к обеим частям второго неравенства число b. Получим верные неравенства: а + с
b + d. Чтобы получить сумму а + с, прибавим к обеим частям первого неравенства число с, а чтобы получить сумму b + d, прибавим к обеим частям второго неравенства число b. Получим верные неравенства: а + с 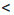 b + с, b + с
b + с, b + с 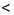 b + d. По свойству 2 из последних двух неравенств следует, что а + с
b + d. По свойству 2 из последних двух неравенств следует, что а + с 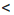 b + d.
b + d.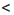 b и с
b и с 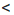 d, где a, b, c и d — положительные числа. Нужно доказать, что ас
d, где a, b, c и d — положительные числа. Нужно доказать, что ас 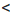 bd. Умножим обе части неравенства а
bd. Умножим обе части неравенства а 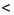 b на положительное число с, а обе части неравенства c
b на положительное число с, а обе части неравенства c 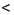 d — на положительное число b. Получим верные неравенства: ас
d — на положительное число b. Получим верные неравенства: ас 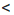 be, be
be, be 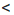 bd. По свойству 2 из последних двух неравенств следует, что ас
bd. По свойству 2 из последних двух неравенств следует, что ас 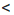 bd.
bd.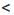 b, а и b — положительные числа, n — натуральное число, то
b, а и b — положительные числа, n — натуральное число, то 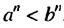
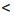 b и почленно их перемножить.
b и почленно их перемножить.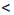 х и 1
х и 1 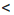 у свойство о почленном сложении неравенств. Получим: 12
у свойство о почленном сложении неравенств. Получим: 12 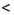 х + у. Применим это же свойство к неравенствам х
х + у. Применим это же свойство к неравенствам х 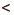 14 и у
14 и у 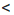 2. Получим: х + у
2. Получим: х + у 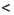 16. Результат запишем в виде двойного неравенства 12
16. Результат запишем в виде двойного неравенства 12 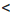 х + у
х + у 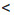 16.
16.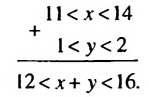
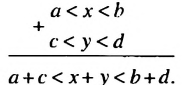
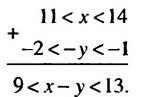
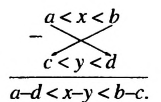
 х
х 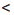 14 и 1
14 и 1 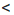 у
у 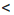 2, то х и у — положительные числа. Применим к неравенству 11
2, то х и у — положительные числа. Применим к неравенству 11 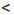 х и 1
х и 1 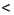 у свойство о почленном умножении неравенств. Получим: 11
у свойство о почленном умножении неравенств. Получим: 11 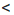 ху. Применим это же свойство к неравенствам х
ху. Применим это же свойство к неравенствам х 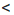 14 и y
14 и y 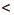 2. Получим: ху
2. Получим: ху 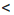 28. Результат запишем в виде двойного неравенства 11
28. Результат запишем в виде двойного неравенства 11 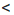 ху
ху 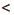 28.
28.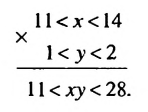
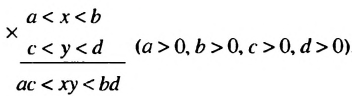
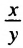 .
.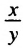 в виде произведения
в виде произведения 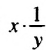 . Поскольку 1
. Поскольку 1 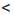 у
у 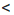 2,
2,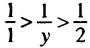 или
или 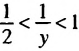 . Согласно свойству о почленном умножении неравенств получим:
. Согласно свойству о почленном умножении неравенств получим: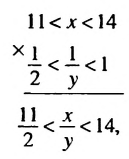
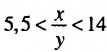 .
.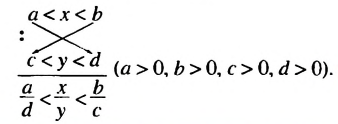
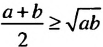 , где а ≥ 0, b ≥ 0.
, где а ≥ 0, b ≥ 0.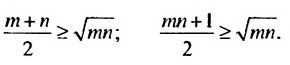
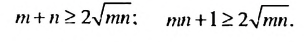
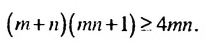
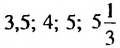 и т. п. Множества решений неравенства иногда можно записывать в виде числовых промежутков.
и т. п. Множества решений неравенства иногда можно записывать в виде числовых промежутков. Рис. 4
Рис. 4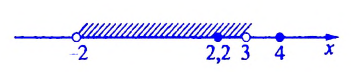 Рис. 5
Рис. 5 Рис. 6
Рис. 6 Рис. 7 а Рис. 7 б
Рис. 7 а Рис. 7 б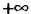 ).
). *Рис. 8
*Рис. 8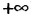 ) (читают: «промежуток от 4 до плюс бесконечности, включая 4»),
) (читают: «промежуток от 4 до плюс бесконечности, включая 4»), Рис. 9
Рис. 9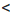 8, записывают (
8, записывают (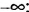 ; 8) и читают «промежуток от минус бесконечности до 8». Множество чисел, удовлетворяющих неравенству х ≤ 8, записывают (
; 8) и читают «промежуток от минус бесконечности до 8». Множество чисел, удовлетворяющих неравенству х ≤ 8, записывают ( Рис. 10 а
Рис. 10 а Рис. 10 б
Рис. 10 б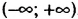
 Рис. 11
Рис. 11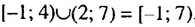 , где
, где 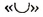 — знак объединения.
— знак объединения.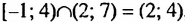 , где
, где 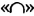 — знак пересечения.
— знак пересечения.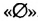 . Записывают:
. Записывают: 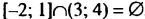 . Объединением промежутков [-2; 1] и (3; 4) является множество
. Объединением промежутков [-2; 1] и (3; 4) является множество 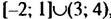 , не являющееся числовым промежутком (оно «состоит» из двух промежутков).
, не являющееся числовым промежутком (оно «состоит» из двух промежутков).
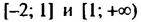 множество общих чисел содержит только одно число — число 1 (см. рис. 13). Такое множество обозначают так: <1>. Записывают:
множество общих чисел содержит только одно число — число 1 (см. рис. 13). Такое множество обозначают так: <1>. Записывают: 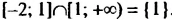 . Легко найти, что
. Легко найти, что 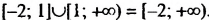 .
. Рис. 13
Рис. 13
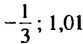 ;
;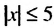 ; б)
; б) 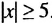 .
.
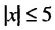 являются все числа, принадлежащие промежутку [-5; 5].
являются все числа, принадлежащие промежутку [-5; 5].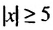 являются числа, которым соответствуют те точки координатной прямой, которые лежат от начала отсчета на расстоянии не меньше 5 (больше 5 или равном 5), то есть значения х, удовлетворяющие неравенству
являются числа, которым соответствуют те точки координатной прямой, которые лежат от начала отсчета на расстоянии не меньше 5 (больше 5 или равном 5), то есть значения х, удовлетворяющие неравенству 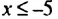 или неравенству
или неравенству 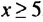 .
.
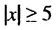 является объединение промежутков
является объединение промежутков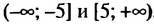 , то есть
, то есть 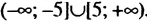
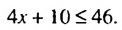
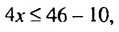
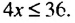
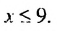
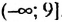 .
. Рис. 16
Рис. 16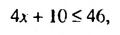
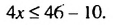
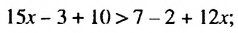
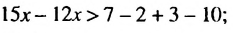
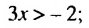
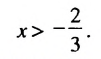

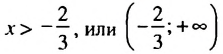
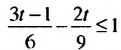 , отметить на координатной прямой множество его решений и записать это множество в виде числового промежутка.
, отметить на координатной прямой множество его решений и записать это множество в виде числового промежутка.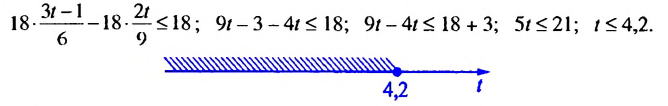
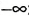 ; 4,2].
; 4,2].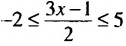 .
.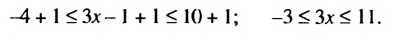
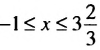 .
.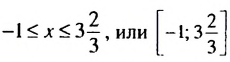 .
.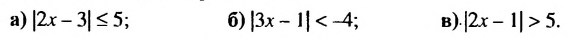
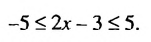
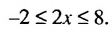
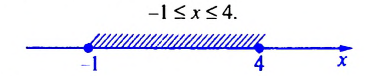
 -2 или неравенству х > 3.
-2 или неравенству х > 3.
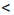 -2 или х > 3. (Ответ можно записать и в виде объединения промежутков:
-2 или х > 3. (Ответ можно записать и в виде объединения промежутков: 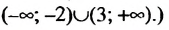
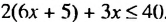 .
.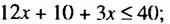
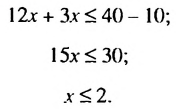
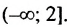
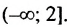
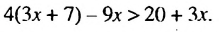
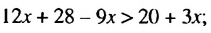
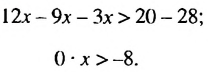
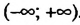
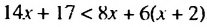 .
.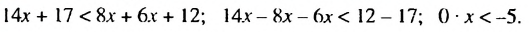
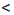 — 5 не имеет решений, так как при любом х значение
— 5 не имеет решений, так как при любом х значение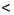 b, ах
b, ах 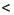 b, где а и b — некоторые известные числа, а х — переменная, называют линейными неравенствами с одной переменной.
b, где а и b — некоторые известные числа, а х — переменная, называют линейными неравенствами с одной переменной.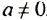 ,то для решения линейного неравенства с одной переменной нужно разделить обе части неравенства на а. Если
,то для решения линейного неравенства с одной переменной нужно разделить обе части неравенства на а. Если 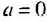 то или решением неравенства является любое число, или неравенство не имеет решений. Выделим следующие основные шаги решения неравенств:
то или решением неравенства является любое число, или неравенство не имеет решений. Выделим следующие основные шаги решения неравенств: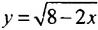 .
.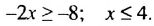
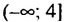 .
.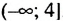
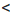 5 с параметром а.
5 с параметром а.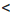 0; 2) а + 3 = 0; 3) а + 3 > 0.
0; 2) а + 3 = 0; 3) а + 3 > 0.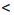 0, то есть а
0, то есть а 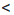 -3, то, разделив обе части неравенства на отрицательное число а + 3, получим:
-3, то, разделив обе части неравенства на отрицательное число а + 3, получим: 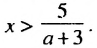
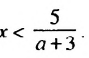
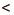 14.
14.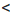 14.
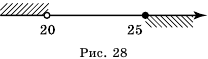
14.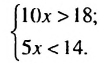
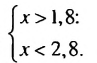
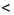 х
х 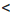 2.8, то есть цена 1 кг помидоров больше 1 руб. 80 к., но меньше 2 руб. 80 к.
2.8, то есть цена 1 кг помидоров больше 1 руб. 80 к., но меньше 2 руб. 80 к.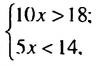
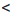 14 является
14 является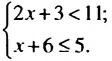
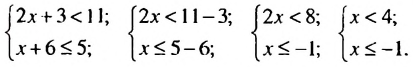
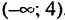 , и множество чисел, удовлетворяющих второму неравенству, — промежуток
, и множество чисел, удовлетворяющих второму неравенству, — промежуток 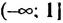 .
.
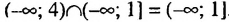
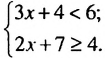
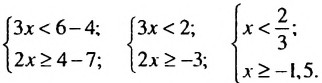
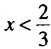 , и множество чисел, удовлетворяющих неравенству
, и множество чисел, удовлетворяющих неравенству 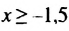 .
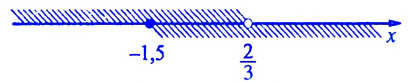
.
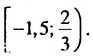
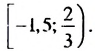
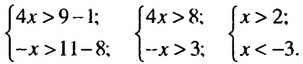
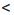 -3.
-3.
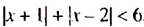 .
.

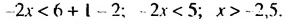
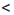 -1, а значит, и
-1, а значит, и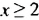 и х
и х 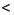 3,5, то есть
3,5, то есть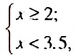 множеством решений которой является промежуток [2; 3,5).
множеством решений которой является промежуток [2; 3,5).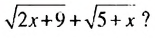
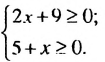

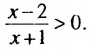

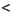 — 1.
— 1.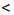 -1 или х > 2. (Множество решений можно записать в виде объединения промежутков:
-1 или х > 2. (Множество решений можно записать в виде объединения промежутков: 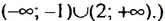
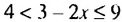 .
.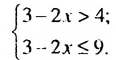
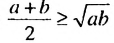 , где а и b рассматривались как длины отрезков.
, где а и b рассматривались как длины отрезков.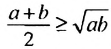 , где а > 0, b > 0.
, где а > 0, b > 0.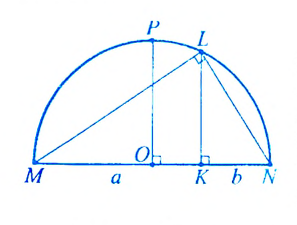
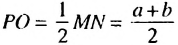 .
.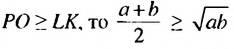 .
.
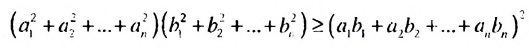
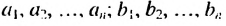 — любые действительные числа.
— любые действительные числа.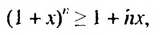
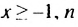 — натуральное число.
— натуральное число.
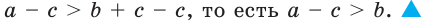
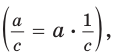 то, учитывая теорему 2.3, можно сделать такой вывод.
то, учитывая теорему 2.3, можно сделать такой вывод.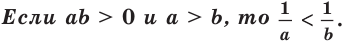
 Разделим обе части неравенства а > b на положительное число ab. Получим правильное неравенство
Разделим обе части неравенства а > b на положительное число ab. Получим правильное неравенство 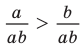 , то есть
, то есть 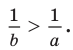 Отсюда
Отсюда 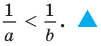
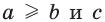 — любое число, то
— любое число, то 

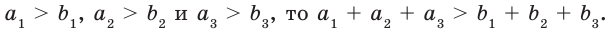
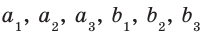 — положительные числа, причем
— положительные числа, причем 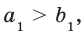
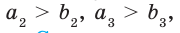 то
то 
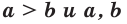 — положительные числа, то
— положительные числа, то 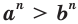 , где
, где 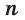 — натурально число.
— натурально число. Запишем
Запишем 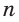 верных неравенств а > b :
верных неравенств а > b :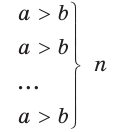 неравенств
неравенств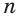 записанных неравенств. Получим
записанных неравенств. Получим 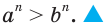
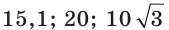 является решением неравенства 14 + 2х > 44, а число 10, например, не является его решением.
является решением неравенства 14 + 2х > 44, а число 10, например, не является его решением.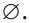
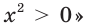 ответ будет таким: «все действительные числа, кроме числа 0».
ответ будет таким: «все действительные числа, кроме числа 0».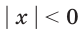 решений не имеет, т. е. множеством его решений является пустое множество.
решений не имеет, т. е. множеством его решений является пустое множество.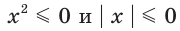 равносильны. Действительно, каждое из них имеет единственное решение х = 0.
равносильны. Действительно, каждое из них имеет единственное решение х = 0.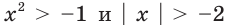 равносильны, так как множеством решений каждого из них является множество действительных чисел.
равносильны, так как множеством решений каждого из них является множество действительных чисел.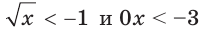 решений не имеет, то они также являются равносильными.
решений не имеет, то они также являются равносильными.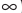 ) (читают: «промежуток от 15 до плюс бесконечности»).
) (читают: «промежуток от 15 до плюс бесконечности»).
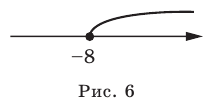
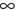 ; либо х > 15.
; либо х > 15.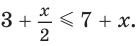
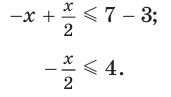
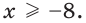
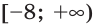 либо
либо 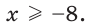
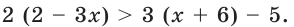
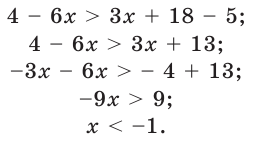
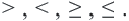 Неравенства могут быть записаны словами или математическими символами, а также изображены на числовой оси.
Неравенства могут быть записаны словами или математическими символами, а также изображены на числовой оси.
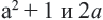 . Для этого рассмотрим разность
. Для этого рассмотрим разность 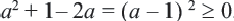 . Значит, при любых значениях переменой значение выражения
. Значит, при любых значениях переменой значение выражения 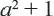 не меньше (больше или равно) значения выражения
не меньше (больше или равно) значения выражения 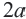 .
. , то
, то 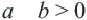 ; если
; если  , то
, то 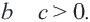 Тогда
Тогда 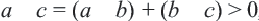 , отсюда следует, что
, отсюда следует, что 

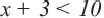

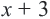 меньше 10.
меньше 10.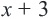 равно 10.
равно 10.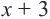 больше 10.
больше 10.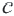
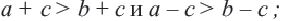
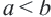 , то для любого числа
, то для любого числа 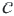
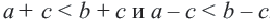 .
.
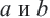 при
при  получим:
получим: получим:
получим:
 прибавить
прибавить 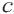 , то
, то 
 прибавить
прибавить 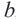 , то
, то 
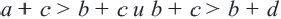 получим, что
получим, что 
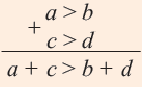
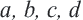 положительные числа,
положительные числа,  и
и  , тогда
, тогда  .
. и
и 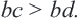
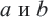 положительные числа и
положительные числа и  . (я-натуральное число).
. (я-натуральное число).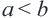 множество всех действительных чисел, удовлетворяющих соотношению
множество всех действительных чисел, удовлетворяющих соотношению 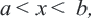 называется интервалом
называется интервалом 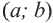
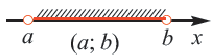 .
.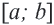 .
.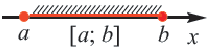
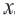 , удовлетворяющих двойному неравенству
, удовлетворяющих двойному неравенству 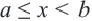 и
и 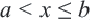 , соответственно записывается как
, соответственно записывается как 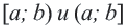 .
.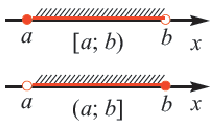
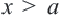 и расположенных справа от точки с координатой
и расположенных справа от точки с координатой 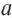 , записывается как
, записывается как 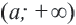 и читается так: промежуток от
и читается так: промежуток от 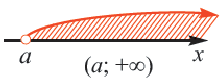
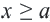 , то это записывается как
, то это записывается как 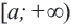 и графически изображается так:
и графически изображается так: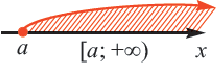
 , записывается как
, записывается как 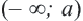 и графически изображается так:
и графически изображается так: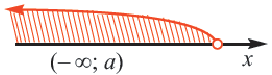
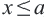 , то это записывается как
, то это записывается как 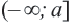 и графически изображается так:
и графически изображается так: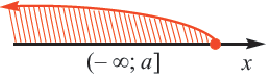
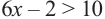 равносильно неравенству
равносильно неравенству  , а неравенство
, а неравенство  равносильно неравенству
равносильно неравенству 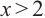 .
.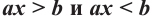 (где
(где 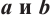 некоторые числа) называются линейными неравенствами, зависящими от одной переменной.
некоторые числа) называются линейными неравенствами, зависящими от одной переменной.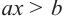
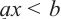
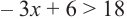
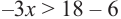
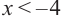 решением неравенства является промежуток
решением неравенства является промежуток 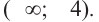
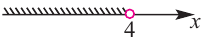

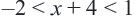 в виде двух неравенств
в виде двух неравенств 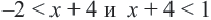
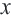 , которые будут удовлетворять неравенствам
, которые будут удовлетворять неравенствам 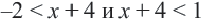 .
.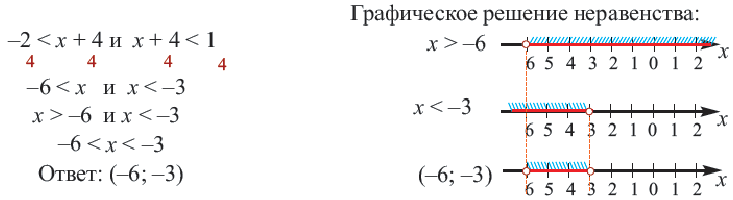
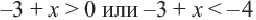
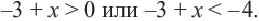
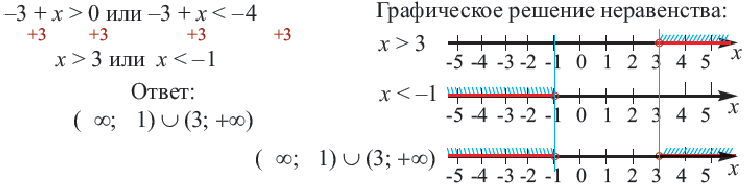
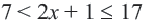 можно решить используя свойства неравенств.
можно решить используя свойства неравенств.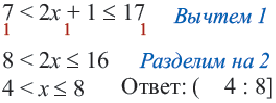
 является множество всех точек, расположенных на расстоянии меньше 3-х единиц от числа 0. Это все действительные числа, которые расположены между числами 3 и 3, т.е.
является множество всех точек, расположенных на расстоянии меньше 3-х единиц от числа 0. Это все действительные числа, которые расположены между числами 3 и 3, т.е. 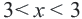 .
.
 неравенство
неравенство  геометрически выражает расстояние от точки 0 до точек
геометрически выражает расстояние от точки 0 до точек 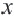 , при котором это расстояние будет меньше
, при котором это расстояние будет меньше 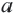 . Оно состоит из множества точек
. Оно состоит из множества точек 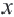 , размещённых на интервале
, размещённых на интервале 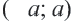 .
.
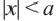 равносильно двойному неравенству
равносильно двойному неравенству 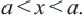 Аналогично, неравенство
Аналогично, неравенство 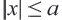 равносильно двойному неравенству
равносильно двойному неравенству 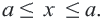
 неравенство
неравенство  геометрически выражает расстояние от точки 0 до точек
геометрически выражает расстояние от точки 0 до точек 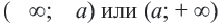 расстояние от начала отсчета до точки
расстояние от начала отсчета до точки 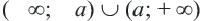 , т.е. объединение промежутков, удовлетворяющее неравенствам
, т.е. объединение промежутков, удовлетворяющее неравенствам 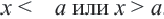 .
.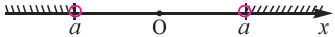
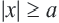 будет
будет 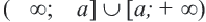 .
.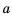 и
и 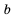 имеет место одно и только одно из соотношений:
имеет место одно и только одно из соотношений: 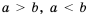 или
или 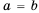 . Ранее в зависимости от вида чисел (натуральные числа, десятичные дроби, обычные дроби с одинаковыми или разными знаменателями) мы использовали то или иное правило сравнения чисел. Удобнее было бы иметь универсальное правило сравнения.
. Ранее в зависимости от вида чисел (натуральные числа, десятичные дроби, обычные дроби с одинаковыми или разными знаменателями) мы использовали то или иное правило сравнения чисел. Удобнее было бы иметь универсальное правило сравнения.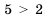 . Рассмотрим разность левой и правой частей этого неравенства:
. Рассмотрим разность левой и правой частей этого неравенства: 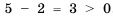 , разность положительна. Рассматривая разность левой и правой частей неравенства
, разность положительна. Рассматривая разность левой и правой частей неравенства 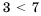 , получаем:
, получаем: 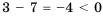 , разность отрицательна. Рассматривая в равенстве
, разность отрицательна. Рассматривая в равенстве 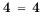 разность левой и правой частей, получим, что разность равна нулю:
разность левой и правой частей, получим, что разность равна нулю: 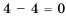 .
.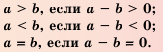
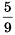 и
и 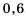 .
.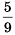 и
и 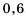 :
: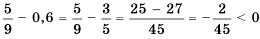
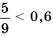 .
.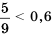
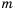 , лежит левее точки, соответствующей числу
, лежит левее точки, соответствующей числу 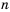 , поэтому
, поэтому 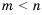 .
.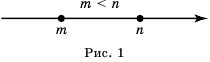
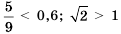 — верные числовые неравенства,
— верные числовые неравенства, 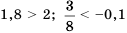 — неверные числовые неравенства.
— неверные числовые неравенства.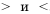 , называемых знаками строгого неравенства, в математике также используют знаки
, называемых знаками строгого неравенства, в математике также используют знаки 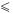 (читают: «меньше или равно» или «не больше») и
(читают: «меньше или равно» или «не больше») и 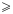 («больше или равно» или «не меньше»). Знаки
(«больше или равно» или «не меньше»). Знаки 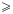 и
и 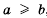 , если
, если 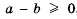 , и
, и 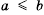 , если
, если 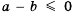 .
.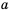 имеет место неравенство
имеет место неравенство 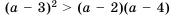 .
.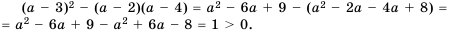 .
.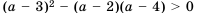 при любом значении
при любом значении 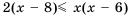 .
.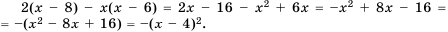 .
.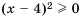 при любом значении
при любом значении 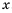 ,
, 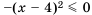 . Следовательно, по определению, неравенство
. Следовательно, по определению, неравенство 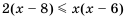 верно при любом
верно при любом 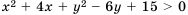 .
.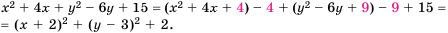 .
.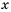 и
и 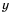 :
: 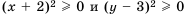 .
.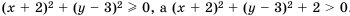 .
. , что и требовалось доказать.
, что и требовалось доказать.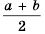 называют средним арифметическим чисел
называют средним арифметическим чисел 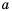 и
и 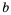 . Для неотрицательных чисел
. Для неотрицательных чисел 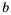 число
число 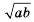 называют их средним геометрическим.
называют их средним геометрическим.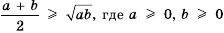 .
.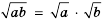 для
для 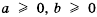 . Получим:
. Получим: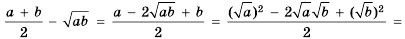
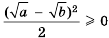 для любых
для любых 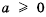 и
и 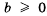 . Следовательно,
. Следовательно, 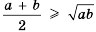 при любых
при любых 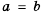 . Если
. Если 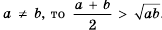 .
. Понятия «больше» и «меньше» появились одновременно с понятием «равно».Еще с древних времен в практической деятельности человека возникла потребность сравнивать количество предметов, длины отрезков, площади участков и т. п. Так, например, несколько неравенств присутствует в выдающемся труде «Начала» древнегреческого математика Евклида (ок. 356-300 до н. э.). В частности, там он доказывает неравенство
Понятия «больше» и «меньше» появились одновременно с понятием «равно».Еще с древних времен в практической деятельности человека возникла потребность сравнивать количество предметов, длины отрезков, площади участков и т. п. Так, например, несколько неравенств присутствует в выдающемся труде «Начала» древнегреческого математика Евклида (ок. 356-300 до н. э.). В частности, там он доказывает неравенство 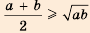 геометрическим методом для положительных чисел
геометрическим методом для положительных чисел 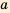 и
и 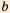 .
.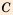 к его диаметру
к его диаметру 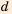 (позже названное числом
(позже названное числом 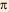 ), другой древнегреческий физик и математик Архимед (ок. 287-212 до н. э.) использовал неравенство:
), другой древнегреческий физик и математик Архимед (ок. 287-212 до н. э.) использовал неравенство: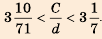 .
. и
и  впервые использовал английский математик Томас Харриот (1560-1621) в работе «Практика аналитического искусства», опубликованной в 1631 году, а знаки
впервые использовал английский математик Томас Харриот (1560-1621) в работе «Практика аналитического искусства», опубликованной в 1631 году, а знаки  и
и  — в 1734 году французский математик и астроном Пьер Бугер (1698-1758).
— в 1734 году французский математик и астроном Пьер Бугер (1698-1758). , где
, где 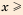 — 1,
— 1, 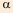 — целое число.
— целое число.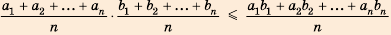 , где
, где 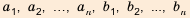 — положительные числа, причем
— положительные числа, причем 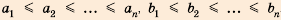 .
.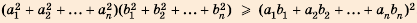 , где
, где 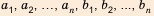 — любые числа.
— любые числа.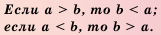
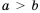 , то
, то 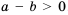 . Тогда
. Тогда 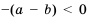 , но
, но 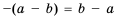 , поэтому
, поэтому 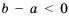 . Следовательно,
. Следовательно, 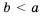 .
.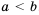 .
.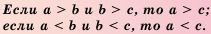
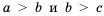 . Поэтому
. Поэтому 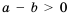 и
и 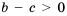 , т. е. числа
, т. е. числа 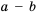 и
и  — положительны. Рассмотрим разность
— положительны. Рассмотрим разность 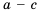 . Имеем:
. Имеем: 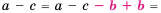
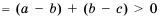 (так как числа
(так как числа 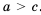 .
.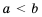 и
и 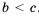 .
.
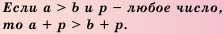
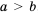 , значит,
, значит, 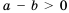 . Рассмотрим разность
. Рассмотрим разность 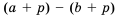 и преобразуем ее:
и преобразуем ее: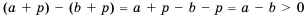 , следовательно,
, следовательно, 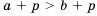 .
.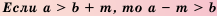 .
.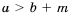 , то
, то 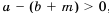 , т.е.
, т.е.  . Но
. Но  , поэтому
, поэтому 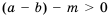 . Следовательно,
. Следовательно, 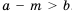 .
.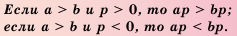
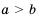 , тогда
, тогда 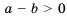 . Рассмотрим разность
. Рассмотрим разность  и преобразуем ее:
и преобразуем ее: 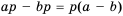 .
.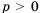 , то
, то 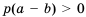 , а значит,
, а значит, 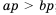 ; если
; если 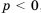 , то
, то 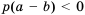 , а значит
, а значит 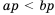 .
.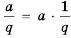 , то, обозначив
, то, обозначив 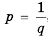 , получим, что аналогичное свойство имеет место и в случае деления обеих частей неравенства на отличное от нуля число
, получим, что аналогичное свойство имеет место и в случае деления обеих частей неравенства на отличное от нуля число 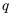 .
.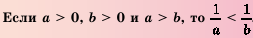
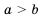 на положительное число
на положительное число 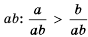 ; тогда
; тогда 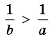 , т. е.
, т. е. 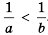 .
.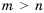 . Сравнить:
. Сравнить: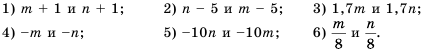
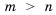 прибавим число 1, то по свойству 3 получим:
прибавим число 1, то по свойству 3 получим: 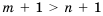 .
.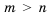 умножим на положительное число 1,7, то по свойству 4 получим верное неравенство
умножим на положительное число 1,7, то по свойству 4 получим верное неравенство 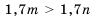 .
.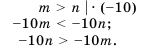
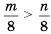 .
.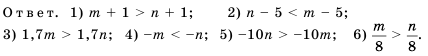
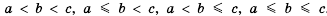 . Например, двойное неравенство
. Например, двойное неравенство 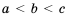 означает, что одновременно имеют место неравенства
означает, что одновременно имеют место неравенства 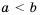 и
и 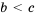 . Так как
. Так как 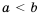 и
и 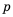 по свойству 3 имеют место неравенства
по свойству 3 имеют место неравенства 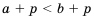 и
и 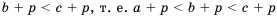 .
.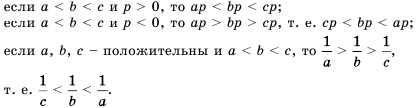
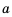 см, если
см, если 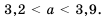
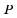 квадрата находят по формуле
квадрата находят по формуле 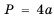 , то все части неравенства
, то все части неравенства 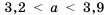 нужно умножить на 4. Получим:
нужно умножить на 4. Получим: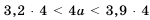 , тогда
, тогда 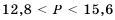 .
.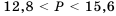 .
.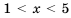 . Оценить значение выражения:
. Оценить значение выражения: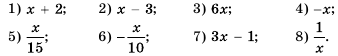
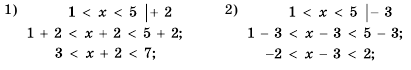
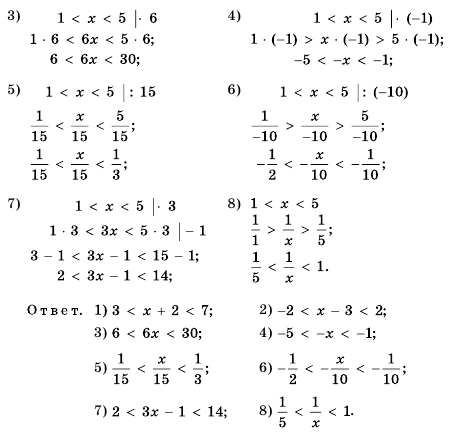
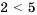 и
и 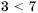 . Сложим их левые части, их правые части и между результатами запишем такой же знак:
. Сложим их левые части, их правые части и между результатами запишем такой же знак: 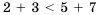 . Получим верное числовое неравенство, ведь, действительно,
. Получим верное числовое неравенство, ведь, действительно, 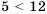 . Действие, которое мы выполнили, называют почленным сложением неравенств. Заметим, что почленно складывать можно лишь неравенства одного знака.
. Действие, которое мы выполнили, называют почленным сложением неравенств. Заметим, что почленно складывать можно лишь неравенства одного знака. и
и  , то
, то  .
.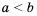 прибавим число
прибавим число 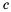 , а к обеим частям неравенства
, а к обеим частям неравенства 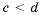 — число
— число 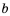 , получим два верных неравенства:
, получим два верных неравенства: 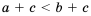 и
и 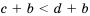 , следовательно,
, следовательно, 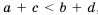 , что и требовалось доказать.
, что и требовалось доказать.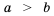 и
и 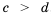 , то
, то 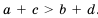 .
.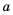 см,
см, 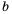 см и
см и 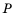 (в см), если
(в см), если 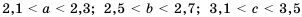 .
.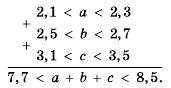
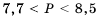 .
.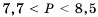 .
. и
и  , где
, где 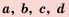 — положительные числа, то
— положительные числа, то  .
.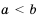 на положительное число
на положительное число 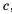 , а обе части неравенства
, а обе части неравенства 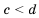 — на положительное число
— на положительное число 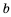 получим два верных неравенства:
получим два верных неравенства: 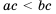 и
и 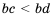 , следовательно,
, следовательно, 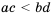 (по свойству 2). Доказано.
(по свойству 2). Доказано.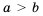 и
и 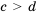 , где
, где 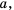
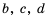 — положительные числа, то
— положительные числа, то 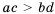 .
. — положительные числа, причем
— положительные числа, причем  , то
, то  , где
, где 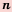 — натуральное число.
— натуральное число.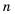 верных неравенств
верных неравенств 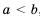 , где
, где 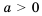 и
и 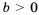 , получим
, получим 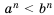 .
.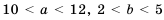 . Оцените значение выражения:
. Оцените значение выражения: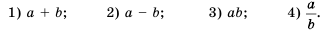
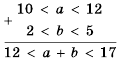
 , представим ее в виде суммы:
, представим ее в виде суммы: 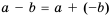 , но сначала оценим выражение
, но сначала оценим выражение 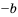 .
.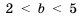 на число
на число 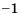 и изменив знаки неравенства на противоположные, получим:
и изменив знаки неравенства на противоположные, получим: 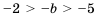 , т. е.
, т. е. 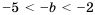 . Таким образом,
. Таким образом,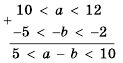
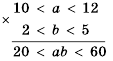
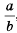 , представим его в виде произведения:
, представим его в виде произведения: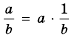 . Оценим выражение
. Оценим выражение 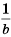 . Если
. Если 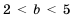 , то
, то 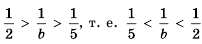 . Таким образом,
. Таким образом, 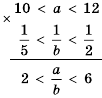 .
.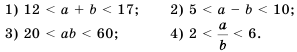
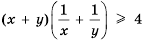 , если
, если 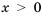 ,
, 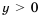
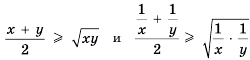
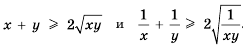 .
.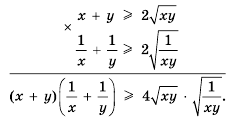
 , что и требовалось доказать.
, что и требовалось доказать.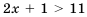 являются, например, числа
являются, например, числа 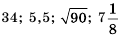 т. д.
т. д.
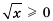 при всех
при всех 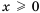 , причем
, причем 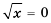 тогда и только тогда, когда
тогда и только тогда, когда 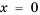 . Значит, решением неравенства
. Значит, решением неравенства 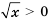 является любое положительное число.
является любое положительное число.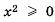 при любом значении
при любом значении 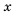 , поэтому
, поэтому 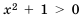 при
при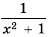 также будет положительным при любом
также будет положительным при любом 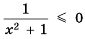 является неверным, т. е. не имеет решений.
является неверным, т. е. не имеет решений.


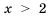 удовлетворяют все числа, большие, чем 2, то есть числа, лежащие на координатной прямой справа от числа 2. Множество этих чисел обозначают
удовлетворяют все числа, большие, чем 2, то есть числа, лежащие на координатной прямой справа от числа 2. Множество этих чисел обозначают 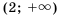 (читают: «промежуток от 2 до плюс бесконечности») и изображают лучом, выходящим из «пустой» точки с координатой 2 (рис. 9).
(читают: «промежуток от 2 до плюс бесконечности») и изображают лучом, выходящим из «пустой» точки с координатой 2 (рис. 9).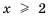 удовлетворяют все числа, большие, чем 2, и само число 2. Множество этих чисел обозначают:
удовлетворяют все числа, большие, чем 2, и само число 2. Множество этих чисел обозначают: 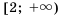 (читают: «промежуток от 2 до плюс бесконечности, включая 2») и изображают лучом, лежащим справа от точки с координатой 2, включая эту точку (рис. 10).
(читают: «промежуток от 2 до плюс бесконечности, включая 2») и изображают лучом, лежащим справа от точки с координатой 2, включая эту точку (рис. 10).
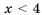 , записывают так:
, записывают так: 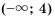 (читают: «промежуток от минус бесконечности до 4»). Это множество изображено на рисунке 11.
(читают: «промежуток от минус бесконечности до 4»). Это множество изображено на рисунке 11.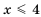 , записывают так: (читают: «промежуток от минус бесконечности до 4, включая 4»). Изображено оно на рисунке 12.
, записывают так: (читают: «промежуток от минус бесконечности до 4, включая 4»). Изображено оно на рисунке 12.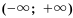 . Множество, не содержащее ни одного числа, обозначают символом
. Множество, не содержащее ни одного числа, обозначают символом 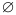 и называют пустым множеством.
и называют пустым множеством.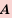 и
и  называют множество, которое состоит из элементов, принадлежащих как множеству
называют множество, которое состоит из элементов, принадлежащих как множеству  .
. . Изображать пересечение множеств удобно в виде диаграмм Эйлера-Венна (рис. 13).
. Изображать пересечение множеств удобно в виде диаграмм Эйлера-Венна (рис. 13).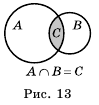
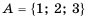 ,
, 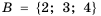 и
и 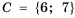 , то
, то 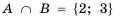 ;
; 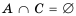 .
.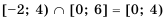 (рис. 14).
(рис. 14).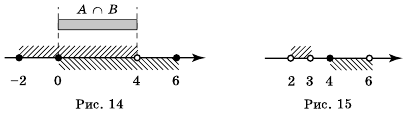
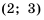 и
и 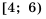 не имеют общих точек (рис. 15), поэтому их пересечением является пустое множество. Записать это можно так:
не имеют общих точек (рис. 15), поэтому их пересечением является пустое множество. Записать это можно так: 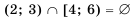 .
. и
и 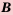 называют множество, которое состоит из всех элементов, принадлежащих хотя бы одному из множеств
называют множество, которое состоит из всех элементов, принадлежащих хотя бы одному из множеств  или
или 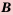 .
. . Изображать объединение множеств также удобно в виде диаграмм Эйлера-Венна (рис. 16).
. Изображать объединение множеств также удобно в виде диаграмм Эйлера-Венна (рис. 16).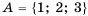 ,
, 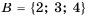 и
и 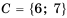 , то
, то 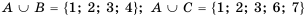 .
.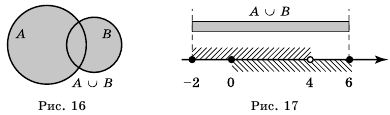
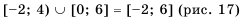 . Отметим, что объединение промежутков не всегда является промежутком. Например, множество
. Отметим, что объединение промежутков не всегда является промежутком. Например, множество 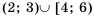 не является промежутком (рис. 15).
не является промежутком (рис. 15).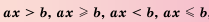 , где
, где  -переменная,
-переменная,  — некоторые числа, называют линейными неравенствами с одной переменной. Если
— некоторые числа, называют линейными неравенствами с одной переменной. Если 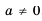 , то обе части неравенства можно разделить на
, то обе части неравенства можно разделить на 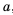 , учитывая при этом свойство числовых неравенств, то есть если а
, учитывая при этом свойство числовых неравенств, то есть если а 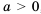 , то знак неравенства оставляем без изменении; если же
, то знак неравенства оставляем без изменении; если же 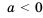 , то знак неравенства изменяем на противоположный.
, то знак неравенства изменяем на противоположный.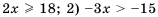 .
.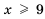 . Таким образом, решением неравенства является промежуток
. Таким образом, решением неравенства является промежуток 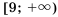 .
.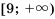 ; 2)
; 2) 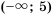 .
.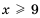 ; 2)
; 2) 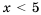 .
.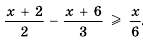
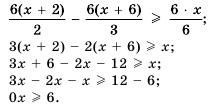
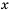 левая часть неравенства будет равна нулю, а неравенство
левая часть неравенства будет равна нулю, а неравенство 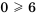 является неверным.
является неверным.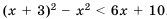 .
.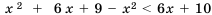 .
.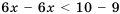 ; то есть
; то есть 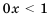 .
.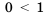 является верным. Таким образом, решением неравенства будет любое число, а значит, множеством решений является промежуток
является верным. Таким образом, решением неравенства будет любое число, а значит, множеством решений является промежуток 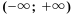 .
.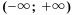 .
.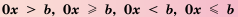 или не имеют решений, или их решение — любое число.
или не имеют решений, или их решение — любое число.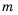 решить неравенство
решить неравенство 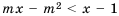 , где
, где 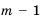 для разных значений
для разных значений 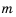 может быть положительным, отрицательным или нулевым, поэтому рассмотрим отдельно каждый из этих случаев:
может быть положительным, отрицательным или нулевым, поэтому рассмотрим отдельно каждый из этих случаев: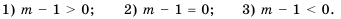
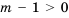 , т. е.
, т. е. 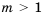 , то, разделив левую и правую части неравенства на положительное число
, то, разделив левую и правую части неравенства на положительное число 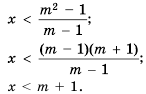
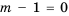 , т. е.
, т. е. 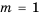 , получим не имеющее решений неравенство
, получим не имеющее решений неравенство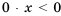 .
.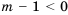 , т. е.
, т. е. 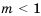 , то, разделив левую и правую части неравенства на отрицательное число
, то, разделив левую и правую части неравенства на отрицательное число  и изменив знак неравенства на противоположный, получим:
и изменив знак неравенства на противоположный, получим: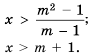
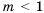 , то
, то 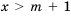 ; если
; если 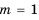 , то решений нет; если
, то решений нет; если 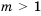 ,то
,то 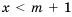 .
.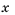 , при которых верным будет как неравенство
, при которых верным будет как неравенство 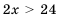 , так и неравенство
, так и неравенство 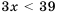 , то есть нужно найти общие решения обоих неравенств. В таком случае объединяют неравенства в систему и говорят, что нужно решить систему неравенств:
, то есть нужно найти общие решения обоих неравенств. В таком случае объединяют неравенства в систему и говорят, что нужно решить систему неравенств: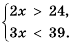
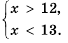
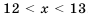 .
.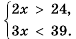
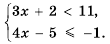
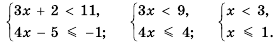
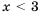 , и множество чисел, удовлетворяющих неравенству
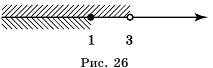
, и множество чисел, удовлетворяющих неравенству 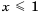 (рис. 26). Множеством решений системы является пересечение этих множеств, то есть промежуток
(рис. 26). Множеством решений системы является пересечение этих множеств, то есть промежуток 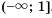 .
.
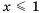 .
.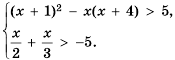
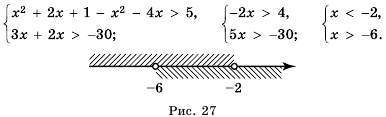
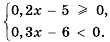
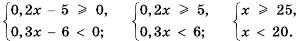
 .
.
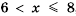 , то есть
, то есть 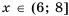 .
.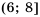 .
.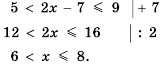
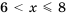 .
.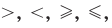 то получим неравенство с переменной. В общем виде неравенство с одной переменной
то получим неравенство с переменной. В общем виде неравенство с одной переменной 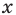 (например, для случая «больше») записывают так:
(например, для случая «больше») записывают так: 
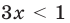 — линейное неравенство;
— линейное неравенство;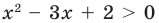 — квадратное неравенство;
— квадратное неравенство;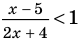 — дробное неравенство
— дробное неравенство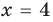 — одно из решений неравенства
— одно из решений неравенства 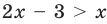 , так как при
, так как при 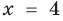 получаем верное неравенство:
получаем верное неравенство: 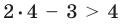 , то есть
, то есть 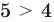
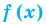 и
и 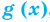 , которые стоят в левой и правой частях неравенства
, которые стоят в левой и правой частях неравенства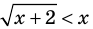 ОДЗ:
ОДЗ: 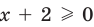 , то есть
, то есть 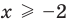 , так как область определения функции
, так как область определения функции 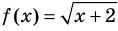 определяется условием:
определяется условием: 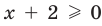 , а областью определения функции
, а областью определения функции 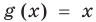 является множество всех действительных чисел
является множество всех действительных чисел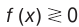 )
)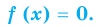
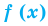 на каждом промежутке, на которые разбивается ОДЗ.
на каждом промежутке, на которые разбивается ОДЗ.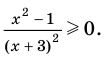
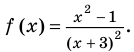
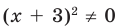 , то есть,
, то есть, 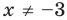 .
.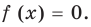
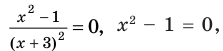
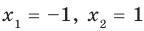 (входят в ОДЗ)
(входят в ОДЗ)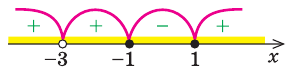
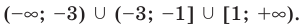
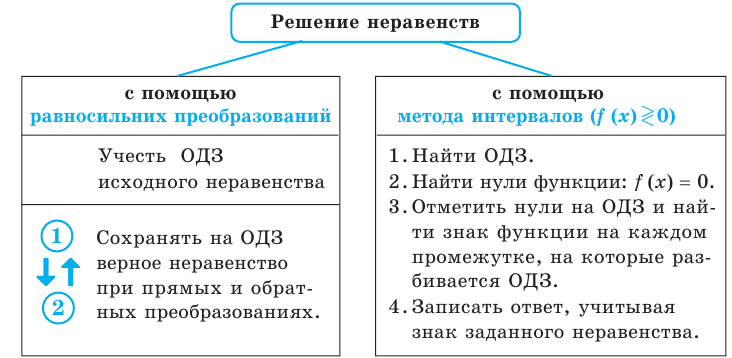
 — исходное неравенство;
— исходное неравенство; — неравенство, полученное в результате преобразования исходного;
— неравенство, полученное в результате преобразования исходного; — символическое изображение выполненных преобразований (с указанием направления их выполнения)
— символическое изображение выполненных преобразований (с указанием направления их выполнения)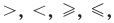 то получаем неравенство с переменной.
то получаем неравенство с переменной.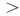 ) чаще всего понимают как аналитическую запись задачи о нахождении тех значений аргументов, при которых значение одной из заданных функций больше, чем значение другой заданной функции. Поэтому в общем виде неравенство с одной переменной
) чаще всего понимают как аналитическую запись задачи о нахождении тех значений аргументов, при которых значение одной из заданных функций больше, чем значение другой заданной функции. Поэтому в общем виде неравенство с одной переменной 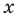 (например, для случаев «больше») записывают так:
(например, для случаев «больше») записывают так: 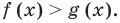
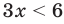 являются все значения
являются все значения 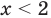 , для неравенства
, для неравенства 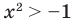 решениями являются все действительные числа (
решениями являются все действительные числа (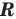 ), а неравенство
), а неравенство 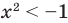 не имеет решений, поскольку значение
не имеет решений, поскольку значение 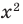 не может быть отрицательным числом, меньшим
не может быть отрицательным числом, меньшим 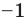 .
.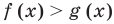 , то общая область определения функций
, то общая область определения функций 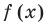 и
и 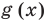 называется областью допустимых значений этого неравенства (иногда используются также термины «область определения неравенства» или «множество допустимых значений неравенства»). Например, для неравенства
называется областью допустимых значений этого неравенства (иногда используются также термины «область определения неравенства» или «множество допустимых значений неравенства»). Например, для неравенства 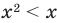 областью допустимых значений являются все действительные числа (это можно записать, например, так: ОДЗ:
областью допустимых значений являются все действительные числа (это можно записать, например, так: ОДЗ: 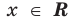 ), поскольку функции
), поскольку функции 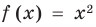 и
и 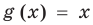 имеют области определения
имеют области определения 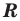 .
.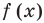 , так и в область определения функции
, так и в область определения функции 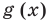 (иначе мы не сможем получить верное числовое неравенство). Таким образом, каждое решение неравенства обязательно входит в ОДЗ этого неравенства. Это позволяет в некоторых случаях применить анализ ОДЗ неравенства для его решения.
(иначе мы не сможем получить верное числовое неравенство). Таким образом, каждое решение неравенства обязательно входит в ОДЗ этого неравенства. Это позволяет в некоторых случаях применить анализ ОДЗ неравенства для его решения.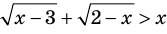 функция
функция 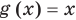 определена при всех действительных значениях
определена при всех действительных значениях 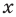 , а функция
, а функция 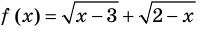 — только при условии, что под знаком квадратного корня будут стоять неотрицательные выражения. Таким образом, ОДЗ этого неравенства задается системой
— только при условии, что под знаком квадратного корня будут стоять неотрицательные выражения. Таким образом, ОДЗ этого неравенства задается системой 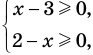 из которой получаем систему
из которой получаем систему 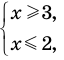 не имеющую решений. Таким образом, ОДЗ заданного неравенства не содержит ни одного числа, поэтому это неравенство не имеет решений.
не имеющую решений. Таким образом, ОДЗ заданного неравенства не содержит ни одного числа, поэтому это неравенство не имеет решений.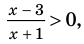
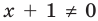 и условие положительности дроби (дробь будет положительной тогда и только тогда, когда числитель и знаменатель дроби имеют одинаковые знаки), а также учесть, что на ОДЗ все необходимые преобразования можно выполнить как в прямом, так и в обратном направлении с сохранением верного неравенства.
и условие положительности дроби (дробь будет положительной тогда и только тогда, когда числитель и знаменатель дроби имеют одинаковые знаки), а также учесть, что на ОДЗ все необходимые преобразования можно выполнить как в прямом, так и в обратном направлении с сохранением верного неравенства.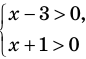 или
или 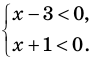 (2)
(2)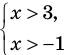 или
или 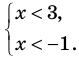
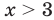 или
или 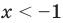 .
. .
.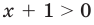 или
или 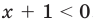 , то
, то 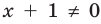 , поэтому в явном виде ОДЗ заданного неравенства не записано при оформлении решения.
, поэтому в явном виде ОДЗ заданного неравенства не записано при оформлении решения. , но его использование при оформлении решений не является обязательным (хотя иногда мы будем его использовать, чтобы подчеркнуть, что было выполнено именно равносильное преобразование).
, но его использование при оформлении решений не является обязательным (хотя иногда мы будем его использовать, чтобы подчеркнуть, что было выполнено именно равносильное преобразование).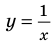 и
и 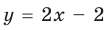 (рис. 54).
(рис. 54).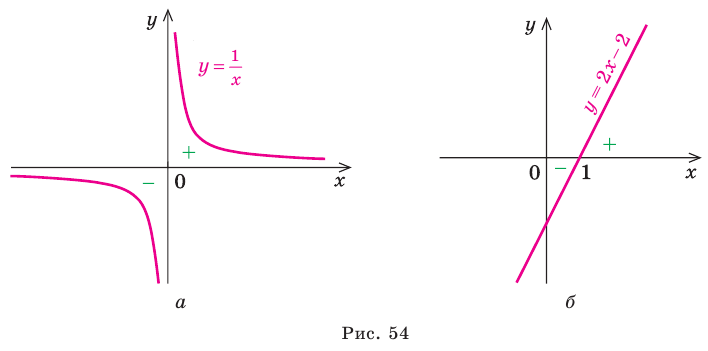
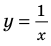 (рис. 54, а) — график разрывается в точке 0 и знак функции изменяется в точке 0);
(рис. 54, а) — график разрывается в точке 0 и знак функции изменяется в точке 0);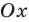 (как в случае функции
(как в случае функции 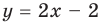 ) (рис. 54, б). На оси
) (рис. 54, б). На оси 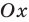 значения функции равны нулю. (Напомним, что значения аргумента, при которых функция равна нулю, называют нулями функции.) Таким образом, любая функция может поменять свой знак только в нулях или в точках, где разрывается график функции (в так называемых точках разрыва функции
значения функции равны нулю. (Напомним, что значения аргумента, при которых функция равна нулю, называют нулями функции.) Таким образом, любая функция может поменять свой знак только в нулях или в точках, где разрывается график функции (в так называемых точках разрыва функции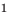 ). Точки, в которых разрывается график функции
). Точки, в которых разрывается график функции 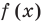 , мы выделяем, как правило, когда находим область определения этой функции. Например, если
, мы выделяем, как правило, когда находим область определения этой функции. Например, если 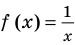 , то ее область определения
, то ее область определения 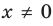 , и именно в точке 0 график этой функции разрывается (рис. 54, а). Если же на каком-нибудь промежутке области определения график функции не разрывается и функция не равна нулю, то по приведенному выше выводу она не может на этом промежутке поменять свой знак
, и именно в точке 0 график этой функции разрывается (рис. 54, а). Если же на каком-нибудь промежутке области определения график функции не разрывается и функция не равна нулю, то по приведенному выше выводу она не может на этом промежутке поменять свой знак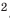 . Таким образом, если отметить нули функции на ее области определения, то область определения разобьется на промежутки, внутри которых знак функции измениться не может (и поэтому этот знак можно определить в любой точке из этого промежутка).
. Таким образом, если отметить нули функции на ее области определения, то область определения разобьется на промежутки, внутри которых знак функции измениться не может (и поэтому этот знак можно определить в любой точке из этого промежутка).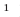 Подробнее это понятие будет рассмотрено в 11 классе.
Подробнее это понятие будет рассмотрено в 11 классе.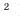 В 11 классе мы уточним формулировку этого свойства (так называемых непрерывных функций). Для всех известных вам функций (линейных, квадратичных, степенных, дробно-рациональных) это свойство имеет место.
В 11 классе мы уточним формулировку этого свойства (так называемых непрерывных функций). Для всех известных вам функций (линейных, квадратичных, степенных, дробно-рациональных) это свойство имеет место.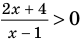 методом интервалов; комментарий, объясняющий каждый этап решения; план решения неравенств вида
методом интервалов; комментарий, объясняющий каждый этап решения; план решения неравенств вида 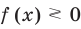 методом интервалов.
методом интервалов.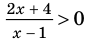
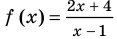
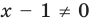 , то есть
, то есть 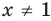
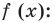
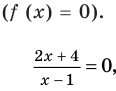
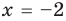 .
.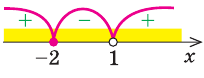
 .
.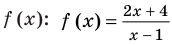 .
.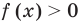 могут быть только числа, которые входят в область определения функции
могут быть только числа, которые входят в область определения функции 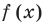 , то есть числа, входящие в ОДЗ неравенства. Поэтому первым этапом решения неравенства методом интервалов будет нахождение его ОДЗ
, то есть числа, входящие в ОДЗ неравенства. Поэтому первым этапом решения неравенства методом интервалов будет нахождение его ОДЗ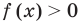 будет нахождение нулей функции (для этого приравниваем функцию
будет нахождение нулей функции (для этого приравниваем функцию 
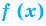
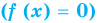
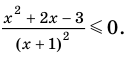
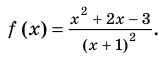
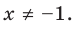
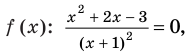
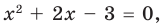
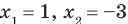 (принадлежат ОДЗ).
(принадлежат ОДЗ).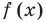 в каждом из промежутков, на которые разбивается ОДЗ.
в каждом из промежутков, на которые разбивается ОДЗ.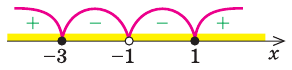 4. Ответ:
4. Ответ: 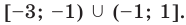
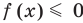 , и для его решения можно применить метод интервалов. Для этого используем план, приведенный выше и в таблице 11.
, и для его решения можно применить метод интервалов. Для этого используем план, приведенный выше и в таблице 11.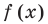 следим за тем, чтобы найденные значения принадлежали ОДЗ (или выполняем проверку найденных корней уравнения
следим за тем, чтобы найденные значения принадлежали ОДЗ (или выполняем проверку найденных корней уравнения 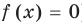 ).
).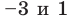 ).
).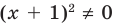 .
.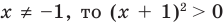 , и тогда в данной дроби знаменатель положителен. Если выполняется данное неравенство, то числитель дроби
, и тогда в данной дроби знаменатель положителен. Если выполняется данное неравенство, то числитель дроби 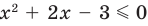 (и наоборот, если выполняется последнее неравенство, то на ОДЗ дробь
(и наоборот, если выполняется последнее неравенство, то на ОДЗ дробь 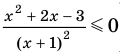 ), то есть данное неравенство равносильно на ОДЗ неравенству
), то есть данное неравенство равносильно на ОДЗ неравенству 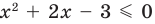 .
.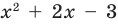 и построим эскиз графика функции
и построим эскиз графика функции 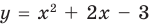 . Решение квадратного неравенства:
. Решение квадратного неравенства: 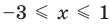 .
.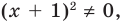 то есть
то есть 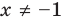 .
.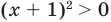 и данное неравенство на его ОДЗ равносильно неравенству
и данное неравенство на его ОДЗ равносильно неравенству 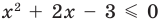 . Поскольку
. Поскольку 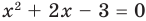 при
при 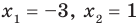 (эти значения
(эти значения 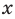 принадлежат ОДЗ), получаем
принадлежат ОДЗ), получаем 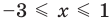 (см. рисунок).
(см. рисунок).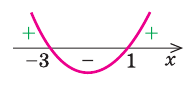
 .
.