Как сделать итерацию в экселе

Метод итераций пример решения excel. С использованием режима «Итерации»

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D x / |A|).

Для расчета Х 1: =U2/$U$1, где U2 – D1. Для расчета Х 2: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

Корень на заданном промежутке один.

РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ с одним неизвестным.

Уравнение с одним неизвестным можно записать в каноническом виде

Метод Ньютона можно рассматривать как некоторую модификацию метода итераций, дающую наилучшую итерирующую функцию g(X) на каждом шаге итерации. Проведем следующие преобразования с исходным каноническим уравнением f(X)=0. Умножим левую и правую его части на некоторое число l, отличное от нуля. Затем прибавим слева и справа по Х. Тогда будем иметь

Дифференцируя g(X), получим g’(X) = 1 + l*f’(X). Из достаточного условия сходимости метода итераций çg’(X)ç 0.

2.2. Метод приближенных вычислений.

Одним из наиболее распространенных итерационных методов решения систем линейных алгебраических уравнений, отличающийся простотой и легкостью программирования, является метод приближенных вычислений или метод Якоби.

Пусть надо решить систему

a 11 x 1 +a 12 x 2 +a 13 x 3 = b 1

a 21 x 1 +a 22 x 2 +a 23 x 3 = b 2

a 31 x 1 +a 32 x 2 +a 33 x 3 = b 3

Предположим, что диагональные элементы a 11, a 22, a 33 отличны от нуля. В противном случае можно переставить уравнения. Выразим переменные из первого, второго и третьего уравнений соответственно. Тогда

Зададим начальные приближения неизвестных

Подставляя их в правую часть преобразованной системы, получим новое первое приближение

Пример 3.1. Найти решение системы линейных алгебраических уравнений (3.1) методом Якоби.

Итерационные методы можно использовать для заданной системы, т.к. выполняется условие «преобладания диагональных коэффициентов», что обеспечивает сходимость этих методов.

Расчетная схема метода Якоби приведена на рис (3.1).

Приведите систему(3.1). к нормальному виду:

, (3.2)

или в матричной форме

, (3.3)

Рис.3.1.

(3.4)

Анализируя результаты, принимаем за приближенное решение исходной системы с заданной точностью e=0,1 четвертую итерацию,

т.е. х 1 =10216; х 2 = 2,0225, х 3 = 0,9912

Изменяя значение e в ячейке Н5 можно получить новое приближенное решение исходной системы с новой точностью.

Проанализируйте сходимость итерационного процесса, построив графики изменения каждой компоненты решения СЛАУ в зависимости от номера итерации.

Аналогично решается система линейных алгебраических уравнений методом Зейделя.

Лабораторная работа №4

Тема. Численные методы решения линейных обыкновенных дифференциальных уравнений с краевыми условиями. Метод конечных разностей

Задание. Решить краевую задачу методом конечных разностей, построив два приближения (две итерации) с шагом h и с шагом h/2.

Проанализировать полученные результаты. Варианты заданий приведены в приложении 4.

Порядок выполнения работы

1. Постройте вручную конечноразностную аппроксимацию краевой задачи (конечноразностную СЛАУ) с шагом h , заданным вариантом.

3. Полученную СЛАУ решите методом прогонки.

5. Уменьшите шаг сетки в 2 раза и еще раз решите задачу. Результаты представьте в графическом виде.

6. Сравните полученные результаты. Сделайте вывод о необходимости продолжения или о прекращении счета.

Решение краевой задачи с использованием электронных таблиц Microsoft Excel.

Пример 4.1. Методом конечных разностей найти решение краевой задачи , y(1)=1, y ’ (2)=0,5 на отрезке xÎ с шагом h=0,2 и с шагом h=0,1. Сравнить полученные результаты и сделать вывод о необходимости продолжения или о прекращении счета.

Расчетная схема для шага h=0,2 приведена на рис.4.1.

Полученное решение (сеточную функцию) Y <1.000, 1.245, 1.474, 1.673, 1.829, 1.930>, Х <1; 1,2; 1,4; 1,6; 1,8;2>в столбце L и B можно принять за первую итерацию (первое приближение) исходной задачи.

Для нахождения второй итерации сделайте сетку вдвое гуще (n=10, шаг h=0,1) и повторите приведенный выше алгоритм.

Сравните полученные приближенные решения. Для наглядности можно построить графики этих двух приближений (двух сеточных функций), рис.4.3.

Порядок построения графиков приближенных решений краевой задачи

1. Постройте график решения задачи для разностной сетки с шагом h=0,2 (n=5).

2. Активизируйте уже построенный график и выберите команду меню Диаграмма\Добавить данные

4. В окне Специальная вставка установите флажки в полях:

Как видно из приведенных данных, два приближенных решения краевой задачи (две сеточные функции) отличаются друг от друга не более, чем на 5%. Поэтому за приближенное решение исходной задачи принимаем вторую итерацию, т.е.

Лабораторная работа №5

Министерство общего образования

Уральский государственный технический университет-УПИ

филиал в г.Краснотурьинске

Кафедра вычислительной техники

По численным методам

Решение линейных уравнений методом простой итерации

c помощью программы Microsoft Excel

Руководитель Кузьмина Н.В.

Студент Нигматзянов Т.Р.

Тема: «Нахождение с заданной точностью корня уравнения F(x)=0 на промежутке методом простой итерации».

Контрольный пример: 0,25-х+sinx=0

Условия задачи: для заданной функции F(x) на интервале найти корень уравнения F(x)=0 методом простой итерации.

Корень вычислить дважды(с помощью автоматического и ручного расчета).

Предусмотреть построение графика функции на заданном интервале.

1.Теоретическая часть 5

2.Описание хода работы 7

3.Входные и выходные данные 8

Библиографический список 12

В ходе данной работы мне необходимо ознакомиться с различными методами решения уравнения и найти корень нелинейного уравнения 0,25-х+sin(x)=0 численным методом – методом простой итерации. Для проверки правильности нахождения корня необходимо решить уравнение графически,найти приближенное значение и сравнить его с полученным результатом.

Метод простой итерации.

Итерационный процесс состоит в последовательном уточнении начального приближения х0 (корня уравнения). Каждый такой шаг называется итерацией.

Для использования этого метода исходное нелинейное уравнение записывается в виде: х=j(х), т.е. выделяется х; j(х) – непрерывна и дифференцируема на интервале (а; в). Обычно это можно сделать несколькими способами:

arcsin(2x+1)-x 2 =0 (f(x)=0)

x=x+arcsin(2x+1)-x 2 (x=j(x))

x= (x=j(x)),знак берется в зависимости от интервала [а;b].

Преобразование должно быть таким, чтобы ½j(x)

Источник

Как работать в Excel с таблицами для чайников: пошаговая инструкция

Программа Microsoft Excel удобна для составления таблиц и произведения расчетов. Рабочая область – это множество ячеек, которые можно заполнять данными. Впоследствии – форматировать, использовать для построения графиков, диаграмм, сводных отчетов.

Работа в Экселе с таблицами для начинающих пользователей может на первый взгляд показаться сложной. Она существенно отличается от принципов построения таблиц в Word. Но начнем мы с малого: с создания и форматирования таблицы. И в конце статьи вы уже будете понимать, что лучшего инструмента для создания таблиц, чем Excel не придумаешь.

Как создать таблицу в Excel для чайников

Работа с таблицами в Excel для чайников не терпит спешки. Создать таблицу можно разными способами и для конкретных целей каждый способ обладает своими преимуществами. Поэтому сначала визуально оценим ситуацию.

Посмотрите внимательно на рабочий лист табличного процессора:

Это множество ячеек в столбцах и строках. По сути – таблица. Столбцы обозначены латинскими буквами. Строки – цифрами. Если вывести этот лист на печать, получим чистую страницу. Без всяких границ.

Сначала давайте научимся работать с ячейками, строками и столбцами.

Как выделить столбец и строку

Чтобы выделить весь столбец, щелкаем по его названию (латинской букве) левой кнопкой мыши.

Для выделения строки – по названию строки (по цифре).

Чтобы выделить несколько столбцов или строк, щелкаем левой кнопкой мыши по названию, держим и протаскиваем.

Для выделения столбца с помощью горячих клавиш ставим курсор в любую ячейку нужного столбца – нажимаем Ctrl + пробел. Для выделения строки – Shift + пробел.

Как изменить границы ячеек

Если информация при заполнении таблицы не помещается нужно изменить границы ячеек:

Для изменения ширины столбцов и высоты строк сразу в определенном диапазоне выделяем область, увеличиваем 1 столбец /строку (передвигаем вручную) – автоматически изменится размер всех выделенных столбцов и строк.

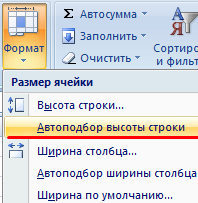
Примечание. Чтобы вернуть прежний размер, можно нажать кнопку «Отмена» или комбинацию горячих клавиш CTRL+Z. Но она срабатывает тогда, когда делаешь сразу. Позже – не поможет.

Чтобы вернуть строки в исходные границы, открываем меню инструмента: «Главная»-«Формат» и выбираем «Автоподбор высоты строки»

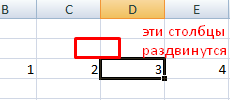
Как вставить столбец или строку

Выделяем столбец /строку правее /ниже того места, где нужно вставить новый диапазон. То есть столбец появится слева от выделенной ячейки. А строка – выше.

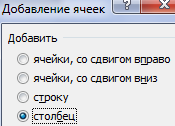
Нажимаем правой кнопкой мыши – выбираем в выпадающем меню «Вставить» (или жмем комбинацию горячих клавиш CTRL+SHIFT+»=»).

Отмечаем «столбец» и жмем ОК.

Совет. Для быстрой вставки столбца нужно выделить столбец в желаемом месте и нажать CTRL+SHIFT+»=».

Все эти навыки пригодятся при составлении таблицы в программе Excel. Нам придется расширять границы, добавлять строки /столбцы в процессе работы.

Пошаговое создание таблицы с формулами

Теперь при печати границы столбцов и строк будут видны.

С помощью меню «Шрифт» можно форматировать данные таблицы Excel, как в программе Word.

Поменяйте, к примеру, размер шрифта, сделайте шапку «жирным». Можно установить текст по центру, назначить переносы и т.д.

Как создать таблицу в Excel: пошаговая инструкция

Простейший способ создания таблиц уже известен. Но в Excel есть более удобный вариант (в плане последующего форматирования, работы с данными).

Сделаем «умную» (динамическую) таблицу:

Примечание. Можно пойти по другому пути – сначала выделить диапазон ячеек, а потом нажать кнопку «Таблица».

Теперь вносите необходимые данные в готовый каркас. Если потребуется дополнительный столбец, ставим курсор в предназначенную для названия ячейку. Вписываем наименование и нажимаем ВВОД. Диапазон автоматически расширится.

Если необходимо увеличить количество строк, зацепляем в нижнем правом углу за маркер автозаполнения и протягиваем вниз.

Как работать с таблицей в Excel

Здесь мы можем дать имя таблице, изменить размер.

Доступны различные стили, возможность преобразовать таблицу в обычный диапазон или сводный отчет.

Возможности динамических электронных таблиц MS Excel огромны. Начнем с элементарных навыков ввода данных и автозаполнения:

Если нажать на стрелочку справа каждого подзаголовка шапки, то мы получим доступ к дополнительным инструментам для работы с данными таблицы.

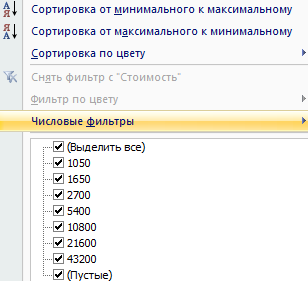
Иногда пользователю приходится работать с огромными таблицами. Чтобы посмотреть итоги, нужно пролистать не одну тысячу строк. Удалить строки – не вариант (данные впоследствии понадобятся). Но можно скрыть. Для этой цели воспользуйтесь числовыми фильтрами (картинка выше). Убираете галочки напротив тех значений, которые должны быть спрятаны.

Источник

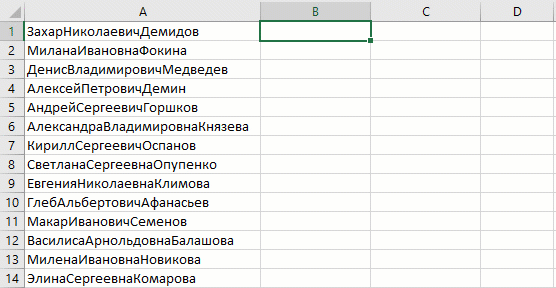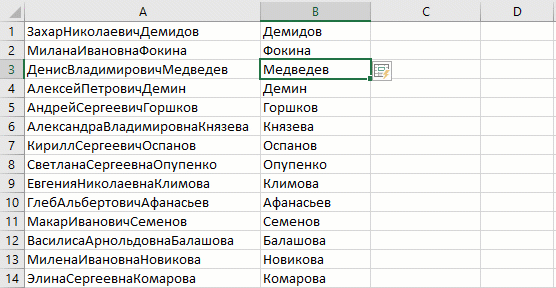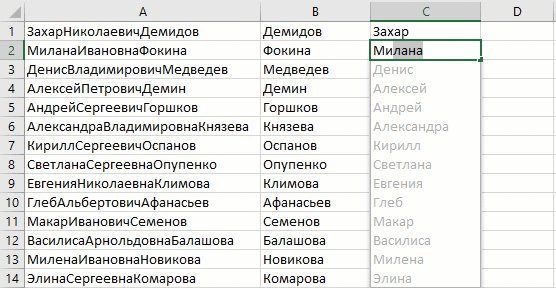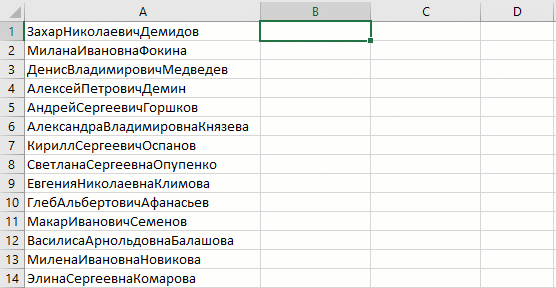
Суперсила Мгновенного заполнения (Flash Fill)

Эксперименты делают из нас героев.
(Флэш)

Механизм работы этого инструмента прост: если у вас есть один или несколько столбцов с исходными данными и вы начинаете набирать рядом в соседнем столбце их же, но в каком-либо нужном вам измененном виде, то Excel рано или поздно намекнёт, что готов продолжить дальше за вас:

Если вы уже ввели 2-3 первых значения, а продолжение всё не появляется, то можно форсировать процесс сочетанием клавиш Ctrl + E или использовать кнопку Мгновенное заполнение (Flash Fill) на вкладке Данные (Data) :

Давайте рассмотрим несколько примеров использования этого инструмента на практике, чтобы понять его возможности.

Извлечение слов из текста и перестановки

Деление текста по регистру

Реализовать подобное формулами очень тяжко. Если без мгновенного заполнения, то поможет только макрос.

Склейка текста

Если можно делить, то можно и клеить! Мгновенное заполнение легко соберёт для вас длинную фразу из нескольких фрагментов, перемежая их нужными пробелами, запятыми, союзами или словами:

Извлечение отдельных символов

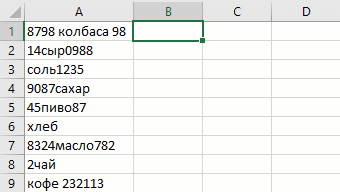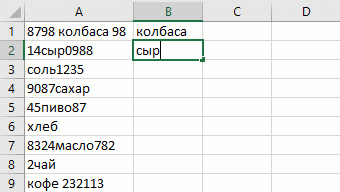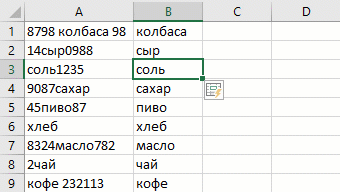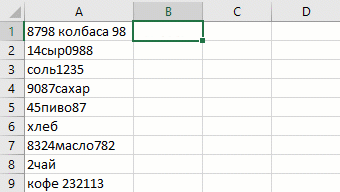
Извлечение только чисел, текста или дат

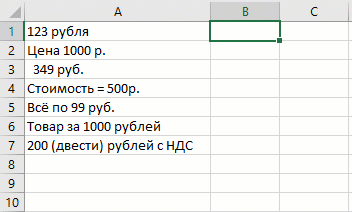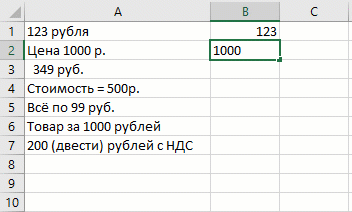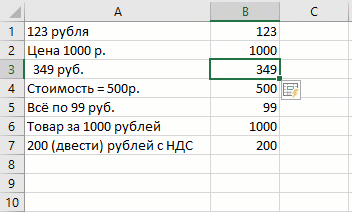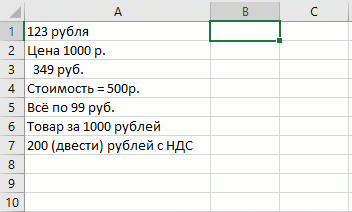
Если вы когда-нибудь пытались вытащить только нужный тип данных из буквенно-цифровой каши, то должны понимать всю сложность этой простой, на первый взгляд, задачи. Мгновенное заполнение и тут справляется «на ура», но нужен лёгкий пендель в виде Ctrl + E :

С извлечением текста тоже самое:

Преобразование форматов чисел или дат

Мгновенное заполнение поможет изменить внешний вид имеющихся данных или привести их к «одному знаменателю». Например, обычную дату преобразовать «шиворот-навыворот» в Unix-формат:

Здесь нюанс в том, что перед вводом нужно заранее поменять формат итоговых ячеек на текстовый, чтобы Excel не пытался распознать введенные вручную в качестве образца «неправильные» даты.

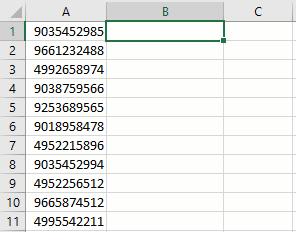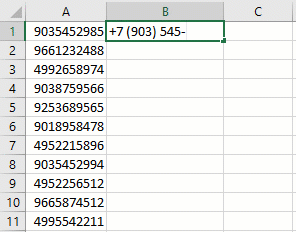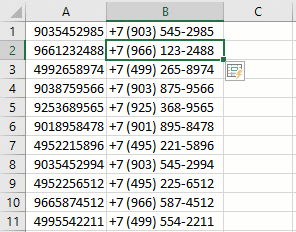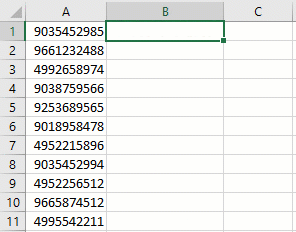
Аналогичным образом можно также правильно представить телефонные номера, добавив код страны и трехзначный префикс оператора (города) в скобках:

Преобразование текста (чисел) в дату

Изменение регистра

Чуть сложнее будет, если нужно изменить регистр по разному у разных частей текста. Например, сделать заглавными только второе слово, оставив первое в нормальном виде. Здесь двух введённых в качестве образца значений окажется недостаточно и придется внести правки, которые мгновенное заполнение тут же учтёт в результатах:

Ограничения и нюансы

При использовании в работе мгновенного заполнения следует помнить несколько моментов:

Источник