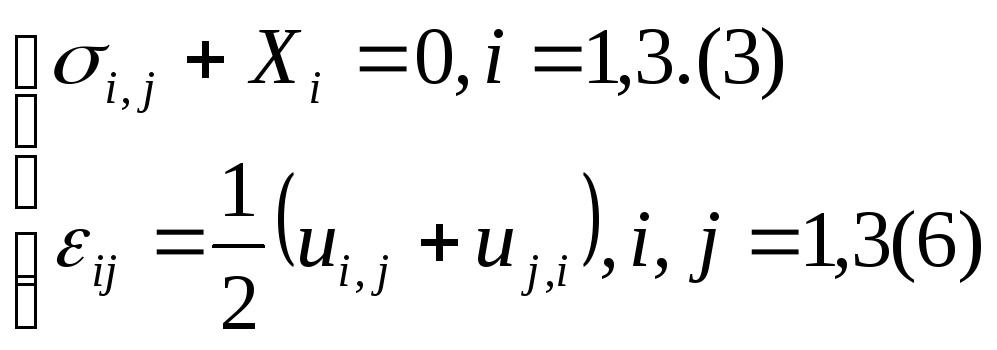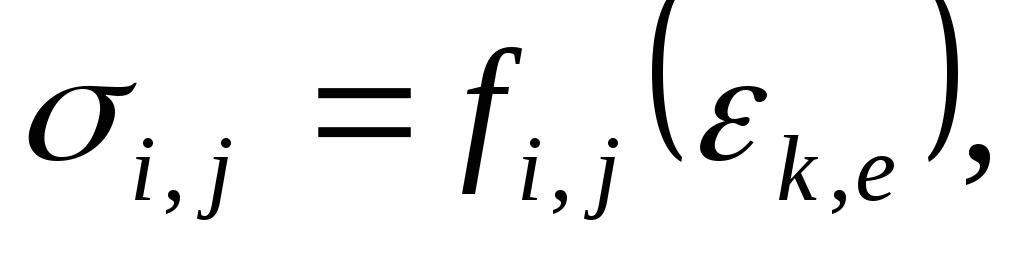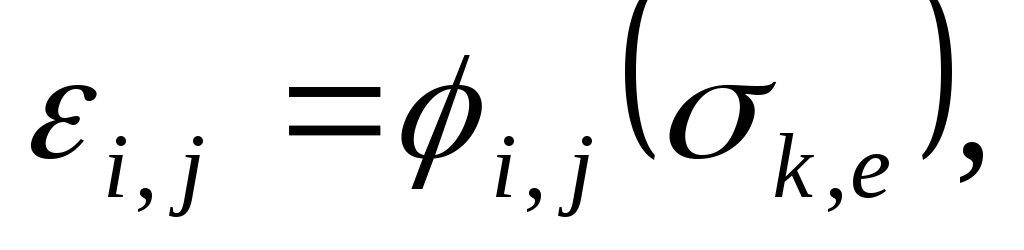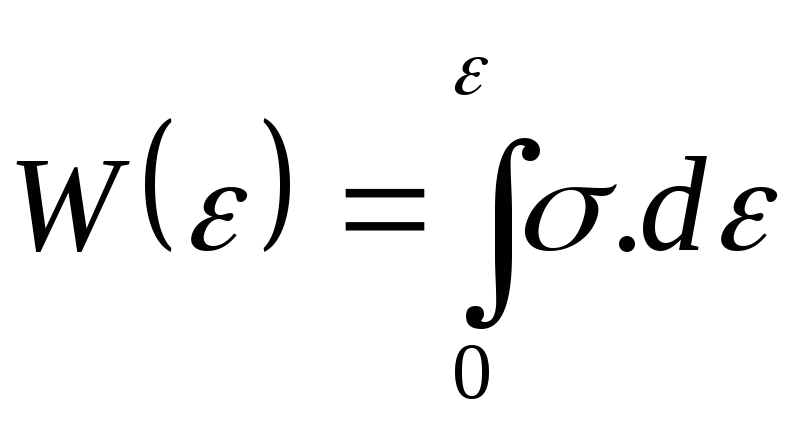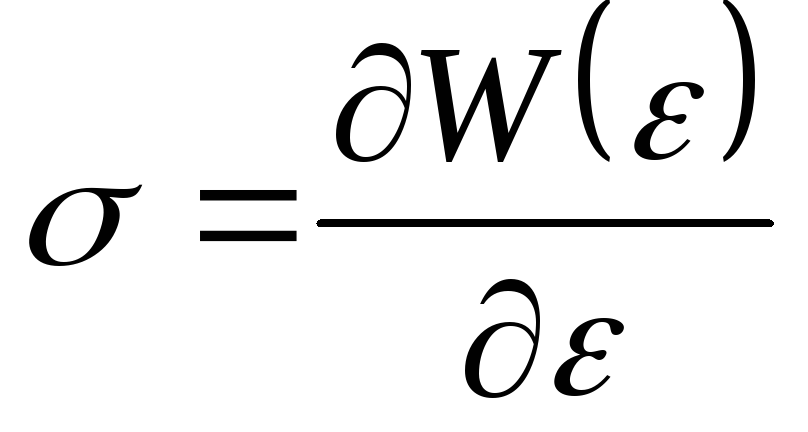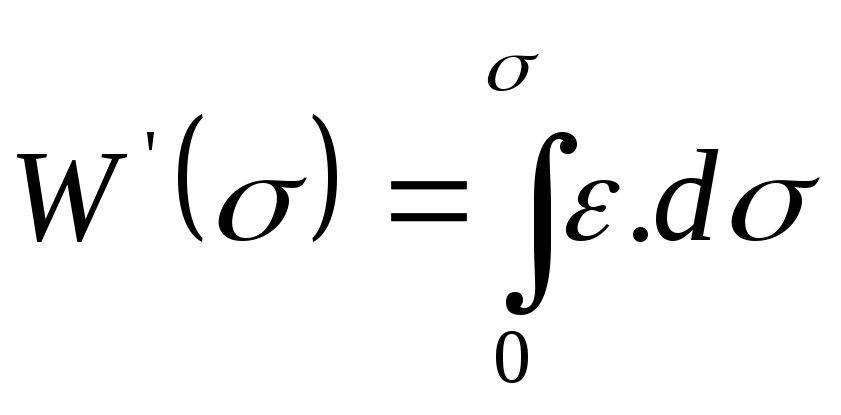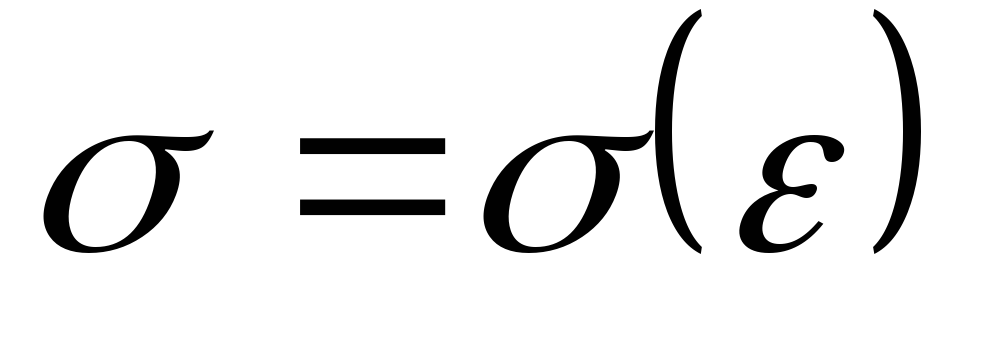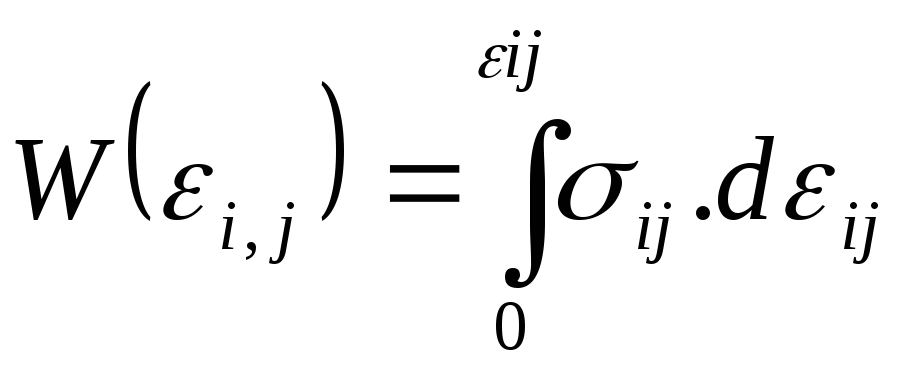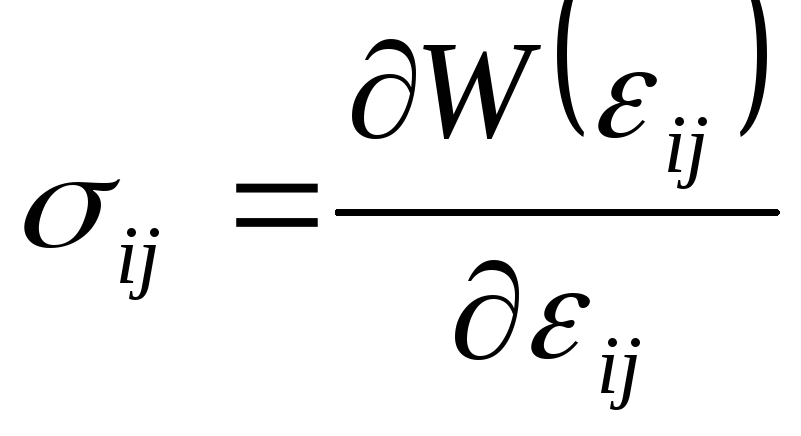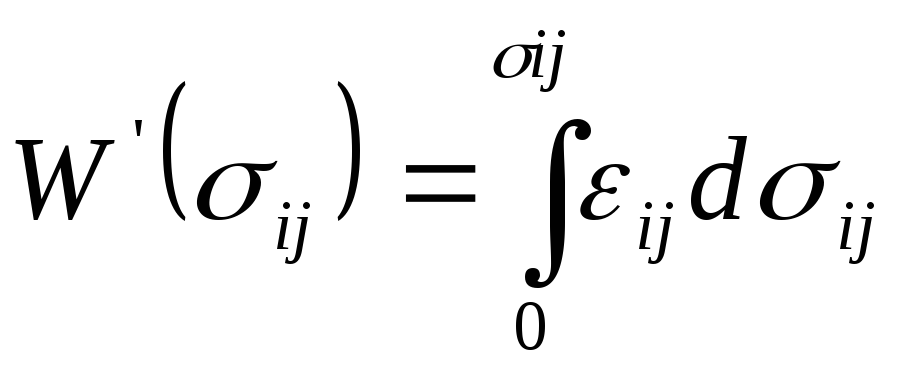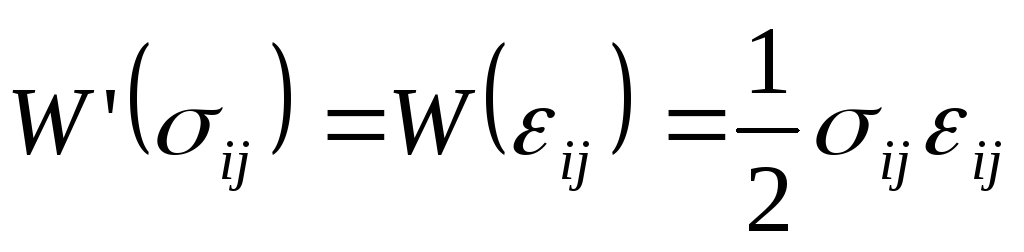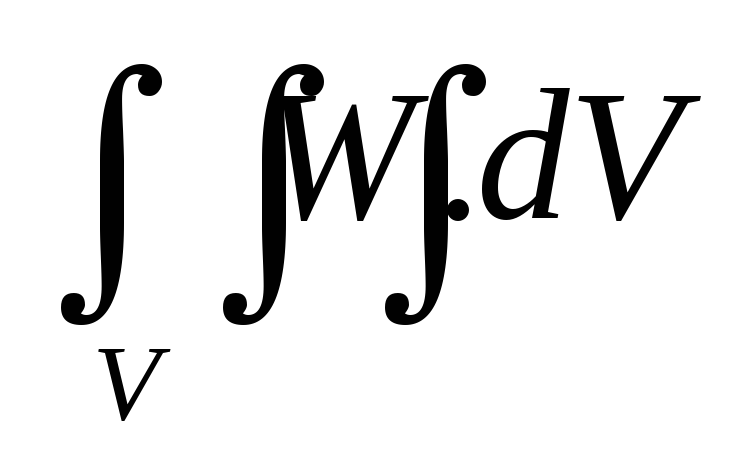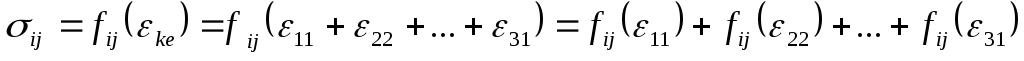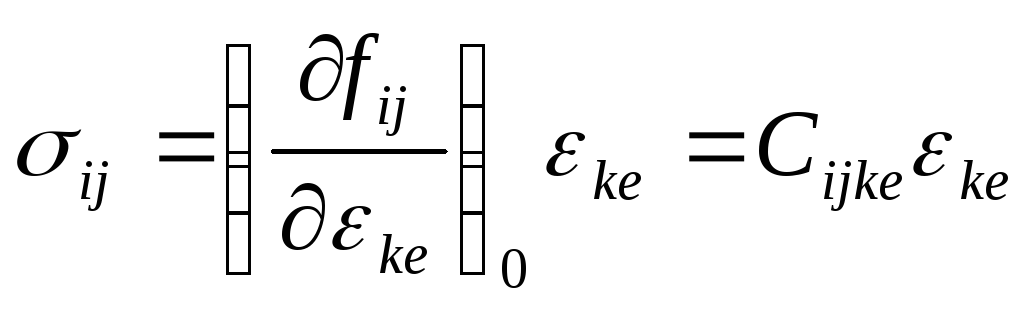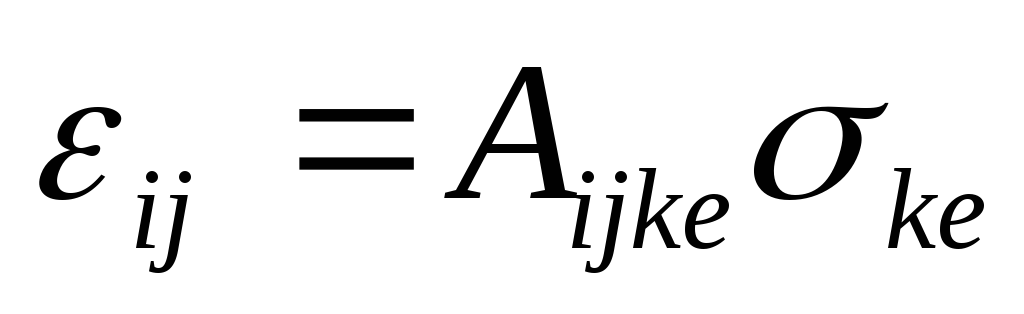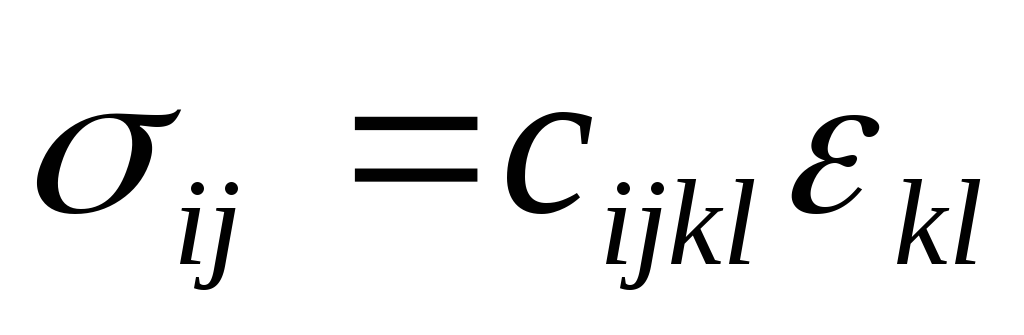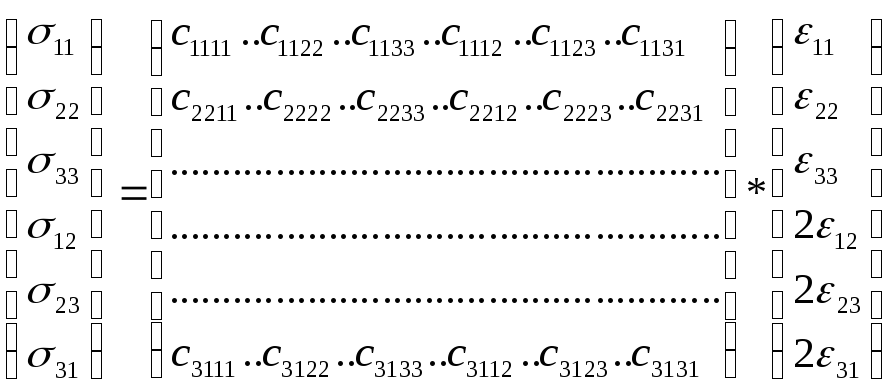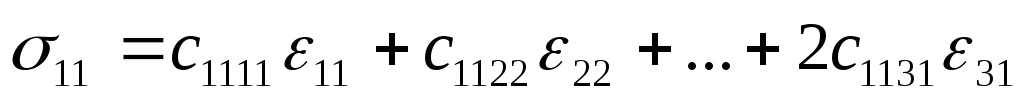закон гука в матричной форме

Закон Гука

Представьте, что вы взялись за один конец упругой пружины, другой конец которой закреплен неподвижно, и принялись ее растягивать или сжимать. Чем больше вы сдавливаете пружину или растягиваете ее, тем сильнее она этому сопротивляется. Именно по такому принципу устроены любые пружинные весы — будь то безмен (в нем пружина растягивается) или платформенные пружинные весы (пружина сжимается). В любом случае пружина противодействует деформации под воздействием веса груза, и сила гравитационного притяжения взвешиваемой массы к Земле уравновешивается силой упругости пружины. Благодаря этому мы можем измерять массу взвешиваемого объекта по отклонению конца пружины от ее нормального положения.

Первое по-настоящему научное исследование процесса упругого растяжения и сжатия вещества предпринял Роберт Гук. Первоначально в своем опыте он использовал даже не пружину, а струну, измеряя, насколько она удлиняется под воздействием различных сил, приложенных к одному ее концу, в то время как другой конец жестко закреплен. Ему удалось выяснить, что до определенного предела струна растягивается строго пропорционально величине приложенной силы, пока не достигает предела упругого растяжения (эластичности) и не начинает подвергаться необратимой нелинейной деформации (см. ниже). В виде уравнения закон Гука записывается в следующей форме:

где F — сила упругого сопротивления струны, x — линейное растяжение или сжатие, а k — так называемый коэффициент упругости. Чем выше k, тем жестче струна и тем тяжелее она поддается растяжению или сжатию. Знак минус в формуле указывает на то, что струна противодействует деформации: при растяжении стремится укоротиться, а при сжатии — распрямиться.

Закон Гука лег в основу раздела механики, который называется теорией упругости. Выяснилось, что он имеет гораздо более широкие применения, поскольку атомы в твердом теле ведут себя так, будто соединены между собой струнами, то есть упруго закреплены в объемной кристаллической решетке. Таким образом, при незначительной упругой деформации эластичного материала действующие силы также описываются законом Гука, но в несколько более сложной форме. В теории упругости закон Гука принимает следующий вид:

где σ — механическое напряжение (удельная сила, приложенная к поперечной площади сечения тела), η — относительное удлинение или сжатие струны, а Е — так называемый модуль Юнга, или модуль упругости, играющий ту же роль, что коэффициент упругости k. Он зависит от свойств материала и определяет, насколько растянется или сожмется тело при упругой деформации под воздействием единичного механического напряжения.

Конечно, закон Гука даже в усовершенствованной Юнгом форме не описывает всего, что происходит с твердым веществом под воздействием внешних сил. Представьте себе резиновую ленту. Если растянуть ее не слишком сильно, со стороны резиновой ленты возникнет возвратная сила упругого натяжения, и как только вы ее отпустите, она тут же соберется и примет прежнюю форму. Если растягивать резиновую ленту и дальше, то рано или поздно она утратит свою эластичность, и вы почувствуете, что сила сопротивления растяжению ослабла. Значит, вы перешли так называемый предел эластичности материала. Если тянуть резину и дальше, через какое-то время она вообще порвется, и сопротивление исчезнет полностью — это вы перешли через так называемую точку разрыва.

Иными словами, закон Гука действует только при относительно небольших сжатиях или растяжениях. Пока вещество сохраняет свои упругие свойства, силы деформации прямо пропорциональны ее величине, и вы имеете дело с линейной системой — каждому равному приращению приложенной силы соответствует равное приращение деформации. Стоит перетянуть резину за предел эластичности, и межатомные связи-пружины внутри вещества сначала ослабевают, а затем рвутся — и простое линейное уравнение Гука перестает описывать происходящее. В таком случае принято говорить, что система стала нелинейной. Сегодня исследование нелинейных систем и процессов является одним из основных направлений развития физики.

Английский физик. Родился во Фрешуотере (Freshwater) на острове Уайт в семье священника, окончил Оксфордский университет. Еще учась в университете, работал ассистентом в лаборатории Роберта Бойля, помогая последнему строить вакуумный насос для установки, на которой был открыт закон Бойля—Мариотта. Будучи современником Исаака Ньютона, вместе с ним активно участвовал в работе Королевского общества, а в 1677 году занял там пост ученого секретаря. Как и многие другие ученые того времени, Роберт Гук интересовался самыми разными областями естественных наук и внес вклад в развитие многих из них. В своей монографии «Микрография» (Micrographia) он опубликовал множество зарисовок микроскопического строения живых тканей и других биологических образцов и впервые ввел современное понятие «живая клетка». В геологии он первым осознал важность геологических пластов и первым в истории занялся научным изучением природных катаклизмов (см. Униформизм). Он же одним из первых высказал гипотезу, что сила гравитационного притяжения между телами убывает пропорционально квадрату расстояния между ними, а это ключевой компонент Закона всемирного тяготения Ньютона, и двое соотечественников и современников так до конца жизни и оспаривали друг у друга право называться его первооткрывателем. Наконец, Гук разработал и собственноручно построил целый ряд важных научно-измерительных приборов — и многие склонны видеть в этом его главный вклад в развитие науки. Он, в частности, первым додумался помещать перекрестье из двух тонких нитей в окуляр микроскопа, первым предложил принять температуру замерзания воды за ноль температурной шкалы, а также изобрел универсальный шарнир (карданное сочленение).

Источник

Сила упругости

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.

Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Деформация

Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил

Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.

Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.

На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.

По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:

Сила упругости: Закон Гука

Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).

При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.

Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, про­порциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.

Закон Гука

Fупр = kx

Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]

Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.

Это равноценные обозначения — можно использовать любое удобное.

Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.

Задачка

На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?

Решение:

Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.

Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :

Тогда из Закона Гука выразим модуль удлинения лески:

Выражаем модуль удлинения:

Подставим числа, жесткость лески при этом выражаем в Ньютонах:

x=3/(0,3 * 1000)=0,01 м = 1 см

Ответ: удлинение лески равно 1 см.

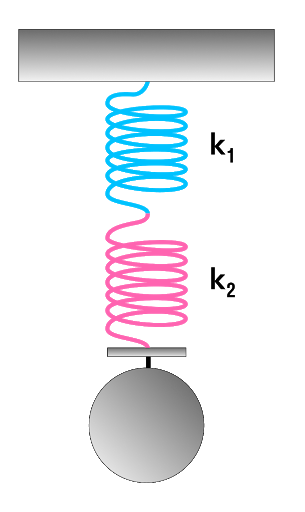
Параллельное и последовательное соединение пружин

В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.

Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.

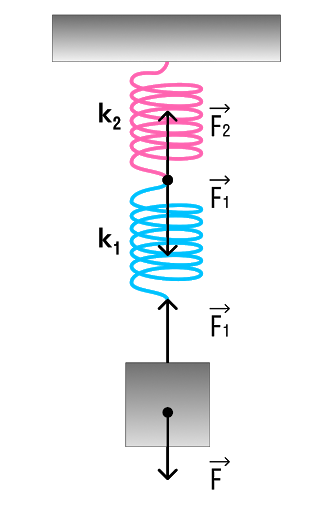
Последовательное соединение системы пружин

Последовательное соединение характерно наличием одной точки соединения пружин.

При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:

Коэффициент жесткости при последовательном соединении пружин

1/k = 1/k₁ + 1/k₂ + … + 1/k_i

k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]

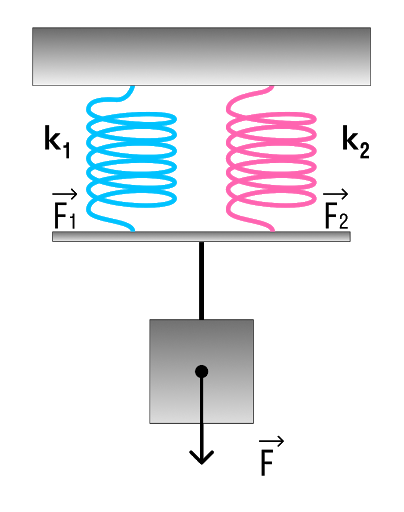
Параллельное соединение системы пружин

Последовательное соединение характерно наличием двух точек соединения пружин.

В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:

Коэффициент жесткости при параллельном соединении пружин

k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]

Задачка

Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?

Решение:

а) Рассмотрим параллельное соединение пружин.

При параллельном соединении пружин общая жесткость

k = k₁ + k₂ = 100 + 200 = 300 Н/м

б) Рассмотрим последовательное соединение пружин.

При последовательном соединении общая жесткость двух пружин

1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015

k = 1000/15 = 200/3 ≃ 66,7 Н/м

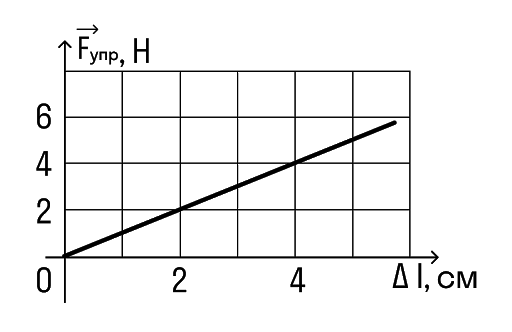
График зависимости силы упругости от жесткости

Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.

Задачка 1

Определите по графику коэффициент жесткости тела.

Решение:

Из Закона Гука выразим коэффициент жесткости тела:

Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.

Например, возьмем вот эту точку.

В ней удлинение равно 2 см, а сила упругости 2 Н.

Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м

Ответ:жесткость пружины равна 100 Н/м

Задачка 2

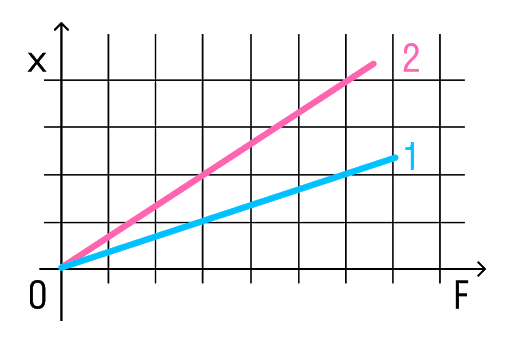
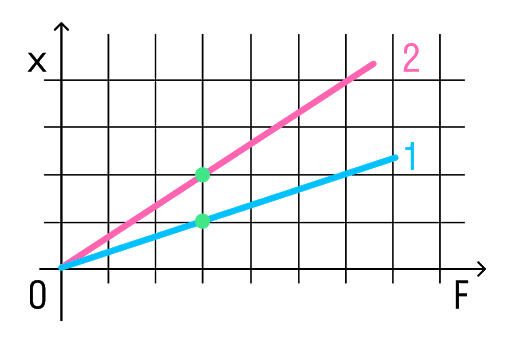
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.

Решение:

Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.

Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.

Значит жесткость стальной проволоки больше.

Ответ: жесткость стальной проволоки больше медной.

Источник

Закон Гука

Механика сплошных сред

Сплошная среда

Классическая механика Закон сохранения массы · Закон сохранения импульса Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнения Навье — Стокса · Уравнение диффузии · Закон Гука Известные учёные Ньютон · Гук Бернулли · Эйлер · Коши · Стокс · Навье

См. также: Портал:Физика

В словесной форме закон звучит следующим образом:

Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации

Для тонкого растяжимого стержня закон Гука имеет вид:

Здесь — сила, которой растягивают (сжимают) стержень, — абсолютное удлинение (сжатие) стержня, а — коэффициент упругости (или жёсткости).

Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения и длины ) явно, записав коэффициент упругости как

Величина называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.

Если ввести относительное удлинение

и нормальное напряжение в поперечном сечении

то закон Гука в относительных единицах запишется как

В такой форме он справедлив для любых малых объёмов материала.

Также при расчёте прямых стержней применяют запись закона Гука в относительной форме

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

Содержание

Обобщённый закон Гука

В общем случае напряжения и деформации описываются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонент). Связывающий их тензор упругих постоянных является тензором четвёртого ранга и содержит 81 коэффициент. Вследствие симметрии тензора , а также тензоров напряжений и деформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом:

где — тензор напряжений, — тензор деформаций. Для изотропного материала тензор содержит только два независимых коэффициента.

Благодаря симметрии тензоров напряжения и деформации, закон Гука может быть представлен в матричной форме.

См. также

Примечания

Ссылки

Полезное

Смотреть что такое «Закон Гука» в других словарях:

ЗАКОН ГУКА — ЗАКОН ГУКА, связь между НАПРЯЖЕНИЕМ и ДЕФОРМАЦИЕЙ в упругом материале при его растяжении. Согласно этому закону, напряжение (сила на единицу площади) пропорционально деформации (изменению в габаритах). Закон приблизителен и применим в… … Научно-технический энциклопедический словарь

закон Гука — Закон, устанавливающий пропорциональность между напряжением и деформацией (см. elastic constant) [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN Hooke s law … Справочник технического переводчика

Закон Гука — – основной закон, устанавливающий в известных пределах прямолинейную зависимость между напряженным состоянием и деформацией упругого тела. [Большая советская энциклопедия. М.: Советская энциклопедия. 1969 1978.] Рубрика термина: Теория и… … Энциклопедия терминов, определений и пояснений строительных материалов

ЗАКОН ГУКА — закон, устанавливающий линейную зависимость между (см.) твёрдого тела и приложенным механическим напряжением. Согласно З. Г. сила упругости, возникающая при деформации тела, пропорциональна удлинению тела и направлена в сторону, противоположную… … Большая политехническая энциклопедия

закон Гука — [Hooke s law] упругая деформация материала прямо пропорциональна приложенному напряжению: εн = σ/Е (для одноосного растяжения) и γ = τ/G (для сдвига), где εн относительная продольная деформация (Δl/l); ΔТ относительный сдвиг; σ нормальное… … Энциклопедический словарь по металлургии

Закон Гука — Hooke s law Закон Гука. Обобщение, применимое ко всем твердым материалам, которое показывает, что напряжение прямо пропорционально деформации и выражается как Е = constant = σ/ε = Напряжение/деформация, где Е модуль упругости (Юнга). Постоянное… … Словарь металлургических терминов

закон Гука — Huko dėsnis statusas T sritis fizika atitikmenys: angl. Hooke’s law vok. Hookesches Gesetz, n rus. закон Гука, m pranc. loi de Hooke, f … Fizikos terminų žodynas

Закон Гука — основной закон теории упругости, выражающий линейную зависимость между напряжениями и малыми деформациями в упругой среде. Установлен P. Гуком (1635 1703) в 1660 г. При растяжении стержня длиной l его удлинение пропорционально растягивающей силе… … Концепции современного естествознания. Словарь основных терминов

закон гука для рiдини при всесторонньому стисненнi — закон Гука для жидкости при всестороннем сжатии Hooke’s law for liquid in all round compression Hookesches Gesetz für die Flüssigkeit bei allseitiger Kompressibilität – змiна об’єму рiдини V при всесторонньому стисненнi прямо пропорцiйна змiнi… … Гірничий енциклопедичний словник

обобщенный закон Гука — [generalized Hooke s law] устанавливает линейную связь между напряжениями и деформациями в любых направлениях, т.е. между каждым компонентом тензора напряжений и каждым компонентом тензора деформаций: εx = [σx μ(σy σz)]E; γxy = τxy/G; εy = [σy… … Энциклопедический словарь по металлургии

Источник

ФДТТ1

3 Связи между напряжениями и деформациями или физические зависимости.

В теории деформаций и в теории напряжений имеем дело с 15-ю функциями координат точек тела, а именно:

i=1,3 –компоненты вектора перемещений (3);

i,j=1,3 – компоненты тензора Коши или тензора малых деформаций(6);

i,j=1,3 – компоненты тензора напряжений(6).

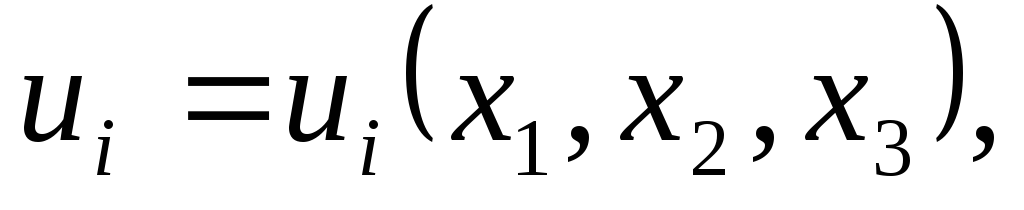
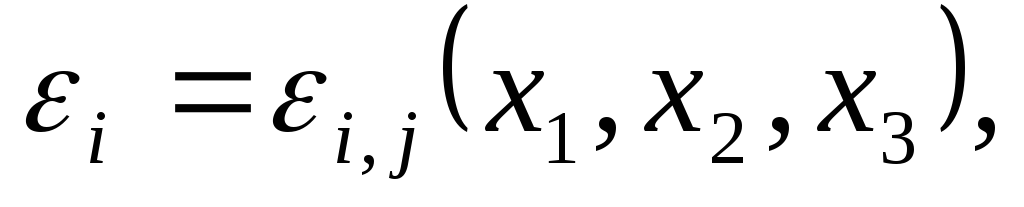
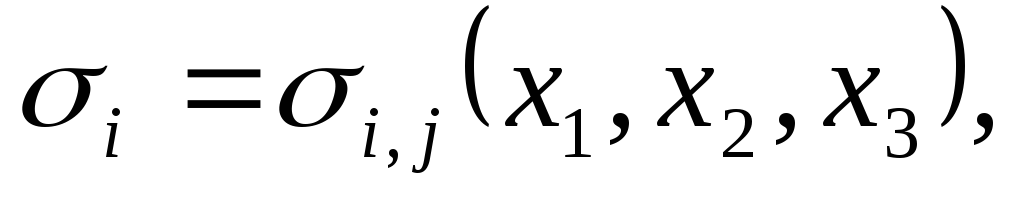
Вывели 9 деформационных зависимостей для любой точки находящейся внутри деформированного твердого тела (дтт).

Уравнения равновесия элементарного параллелепипеда

Х_i – компоненты вектора интенсивности внешних объемных сил,

Система 9-ти дифференциальных уравнений является незамкнутой или недоопределенной должна быть заполнена зависимостями между напряжениями и деформациями. Они получаются в результате механических испытаний. Для разных материалов они разные. Взаимно-однозначная связь между напряжениями и деформациями называется законом упругости:

Причем состояние, когда при нулевых аргументах функции деформаций и функции напряжений равны нулю, то есть 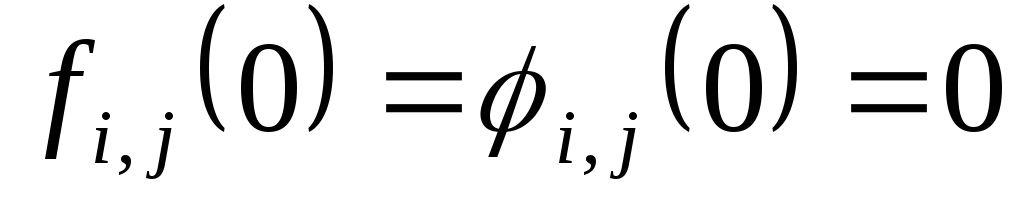называется естественным состоянием.

Под действием внешнего нагружения твердое тело деформируется, то есть изменяет свои первоначальные размеры и формы, при снятии внешнего нагружения оно может восстанавливать свои первоначальные размеры и форму или, как говорят, деформация обратима; если не восстанавливает – деформация необратима.

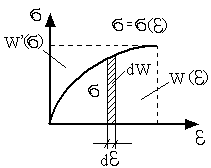
Упругий потенциал. Линейный потенциал. Удельная дополнительная потенциальная энергия деформации. Потенциальная энергия деформации тела.

Рассмотрим одноосное или линейное напряженное состояние элементарного параллелепипеда выделенного в окрестности любой точке деформированного твердого тела.

Нелинейное упругое тело (материал)

-упругий потенциал или удельная потенциальная энергия деформации или потенциальная энергия деформации элементарного параллелепипеда выделенного в окрестности рассматриваемой точки. Причем:

если известен W(ε) то напряжение может быть найдено по следующей формуле:

Линейно упругое тело (материал)

— линейный потенциал или потенциальная энергия линейно-упругого деформирования элементарного параллелепипеда в окрестности рассматриваемой точки деформированного твердого тела.

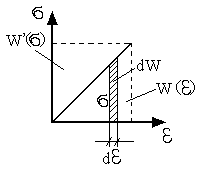
Удельная дополнительная потенциальная энергия

характеристика немеющая механического смысла определяемая представленным образом; равняется площади под кривой

удельная дополнительная потенциальная энергия и линейный потенциал совпадают по величине.

Рассмотрим медленное или статическое многократное нагружение элементарного параллелепипеда в окрестности произвольной точки деформированного твердого тела

Повторяющиеся индексы представляют собой суммирование.

Причем W(0)=0, если известен упругий потенциал W(ε_ij) то напряжения могут быть найдены по формуле Грина:

П=

— потенциальная энергия деформации тела.

Для одноосного напряженного состояния связь между напряжением и деформацией была получена экспериментально в 1660 году английским физиком-математиком Робертом Гуком.

— закон Гука для однородного изотропного тела при линейно напряженном состоянии Е=const

Закон Гука для ЛНС может быть распространен и на многократное напряженное состояние с учетом следующих гипотез:

Гипотеза относительной жесткости

согласно которой функции деформаций (аналогично напряжений) являются непрерывными функциями и в окрестности естественного состояния могут быть разложены в ряд Тейлора, то есть

тензорная форма представления закона Гука, где

— тензоры второго ранга, соответственно, напряжений и деформаций, содержат 3 2 =9 компонент, из которых 6 являются линейно независимыми.

(), () – тензоры четвертого ранга, соответствующие, коэффициентам жесткости или упругости и податливости 3 4 =81 компонент, из которых в силу симметричности тензоров напряжений и деформаций линейно независимыми являются 36.

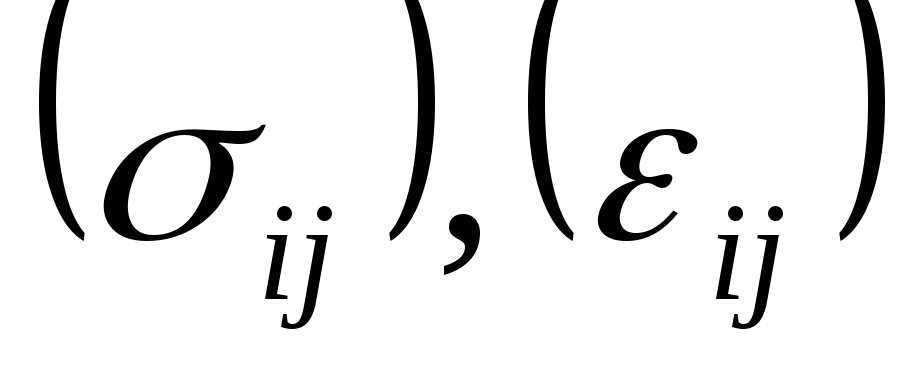
Существует также векторно-матричная форма представления закона Гука. Формально выглядит следующим образом:

1 – вектор напряжений;

2 – матрица коэффициентов жесткости или упругости (6х6), является симметрично относительно главной диагонали, т. е. из 36 коэффициентов линейно независимыми являются 21 коэффициент;

3 – вектор деформаций.

Однородное тело – тело (материал, среда), у которого упругие свойства не зависят от координат точек тела, то есть являются постоянными величинами (=соnst). Неоднородное тело – тело, упругие свойства которого зависят от координат точек тела (=(х₁х₂х₃х₄), Е=Е(х₁х₂х₃)). Изотропное (анизотропное)тело – тело, у которого упругие свойства не зависят от направления в любой точке (зависят от направления).

Тело может быть однородным или неоднородным и одновременно изотропным или анизотропным.

Если оси ЛСК совпадают с осями упругой симметрии тела (оси относительно которых свойства материала или тела являются симметричными или одинаковыми),то число коэффициентов жесткости или податливости являющихся линейно независимыми, становятся меньше, так как некоторые из коэффициентов зануляются, а некоторые являются одинаковыми.

Рассмотрим одну плоскость упругой симметрии, например:

Тогда упругий потенциал должен быть инвариантен к преобразованию вида:

то есть коэффициенты матрицы жесткости или податливости стоящие перед деформациями, меняющими знак должны быть равны нулю, а это коэффициенты у которых индекс 3 встречается 1-3 раза.

Источник